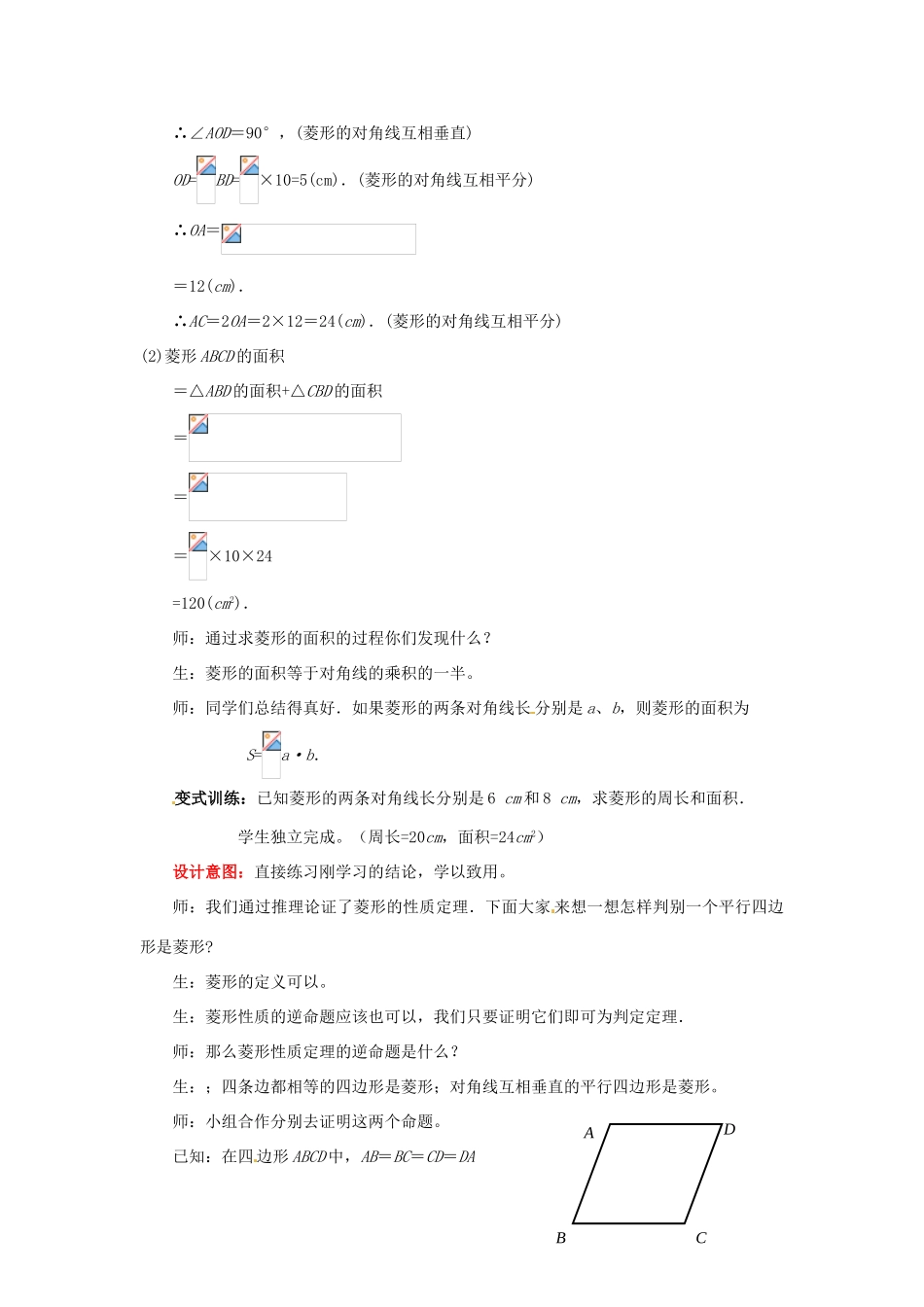
3.2特殊的平行四边形(2)教学过程想一.巧设情境引入新知师:上节课我们学习了一类特殊的平行四边形—矩形,我们以前还接触过哪类特殊的平行四边形?生:菱形.师:那什么样的四边形是菱形呢?生:有一组邻边相等的平行四边形是菱形.师:因为菱形是特殊的平行四边形,所以它不仅具有平行四边形的所有性质,而且具有它本身独特的性质.你还记得菱形的那些性质?我们按照边、角、对角线的顺序回忆。生:菱形的对边平行,四条边都相等,对角相等,对角线互相平分、垂直,并且每条对角线平分一组对角.生:还有菱形既是中心对称图形,又是轴对称图形.师:这些性质在以前的学习中都是通过折纸、猜想等活动归纳出来的。本节课我们来验证明这些性质。板书课题---§3.2特殊的平行四边形设计意图:通过提问让学生明白菱形属于特殊平行四边形的一种,对于菱形的学习可以类比矩形的学习,让学生在心理上感觉本节课的内容很容易接受。二.小组合作探究学习课题课型新授课授课时间教学目标1.菱形的性质定理的证明.2.菱形的判定定理的证明.3.体会证明过程中所运用的归纳概括以及转化等数学思想方法.重点、难点教学重点:菱形的性质及判定定理的证明.教学难点:菱形的性质及判定定理的证明.教法及学法小组合作探究课前准备教师制作课件师:同学们是怎么理解“菱形的四条边相等”生:因为菱形是特殊的平行四边形,所以它不仅具有平行四边形的所有性质,而且具有它本身独特的性质,菱形的对边相等邻边也想等所以四条边都相等。师:谁能说出这个性质的已知、求证呢?如图,已知四边形ABCD是菱形,求证:AB=BC=CD=DA.找同学口述证明过程定理:菱形的四条边相等。师:“菱形的对角线互相垂直,并且每条对角线平分一组对角”对于这一性质呢?如图:已知在菱形ABCD中,对角线AC和BD相交于点O,求证:AC⊥BD,AC平分∠BAD和∠BCDBD平分∠ABC和∠ADC.证明: 四边形ABCD是菱形∴AB=BC=DA=DC∴AC⊥BD(到线段两段距离相等的点在线短的垂直平分线上)∴∠BAC=∠DAC(三线合一)同理∠BCA=∠DCA∠ABD=∠CBD∠ADB=∠CDB即:AC平分∠BAD和∠BCDBD平分∠ABC和∠ADC.定理:菱形的对角线互相垂直,并且每条对角线平分一组对角。师:接下来我们来看一个例题以熟悉巩固菱形的性质定理。例:如图,四边形ABCD是边长为13cm的菱形,其中对角线BD长10cm,求:(1)对角线AC的长度;(2)菱形ABCD的面积.学生小组合作探究,教师巡视点拨,指定同学到黑板板书。解:(1) 四边形ABCD是菱形,ABCDADCBOABCDE∴∠AOD=90°,(菱形的对角线互相垂直)OD=BD=×10=5(cm).(菱形的对角线互相平分)∴OA==12(cm).∴AC=2OA=2×12=24(cm).(菱形的对角线互相平分)(2)菱形ABCD的面积=△ABD的面积+△CBD的面积===×10×24=120(cm2).师:通过求菱形的面积的过程你们发现什么?生:菱形的面积等于对角线的乘积的一半。师:同学们总结得真好.如果菱形的两条对角线长分别是a、b,则菱形的面积为S=a·b.变式训练:已知菱形的两条对角线长分别是6cm和8cm,求菱形的周长和面积.学生独立完成。(周长=20cm,面积=24cm2)设计意图:直接练习刚学习的结论,学以致用。师:我们通过推理论证了菱形的性质定理.下面大家来想一想怎样判别一个平行四边形是菱形?生:菱形的定义可以。生:菱形性质的逆命题应该也可以,我们只要证明它们即可为判定定理.师:那么菱形性质定理的逆命题是什么?生:;四条边都相等的四边形是菱形;对角线互相垂直的平行四边形是菱形。师:小组合作分别去证明这两个命题。已知:在四边形ABCD中,AB=BC=CD=DAABCD求证:四边形ABCD是菱形.已知:在四边形ABCD中,对角线AC⊥BD.求证:四边形ABCD是菱形.学生交流后,利用菱形的定义完成书写步骤设计意图:把课后习题以课堂问题的形式展开,让学生在课堂接受,构建知识结构。三.盘点收获1.通过本节课的学习,哪些是你记忆深刻的?这节课我们主要证明了菱形的性质定理和判定定理.菱形的性质定理:①菱形的四条边相等.②菱形的对角线互相垂直,并且每条对角线平分一组对角.菱形的判定定理:①对角线互相垂直的平行四边形是菱形.②四条边都相...