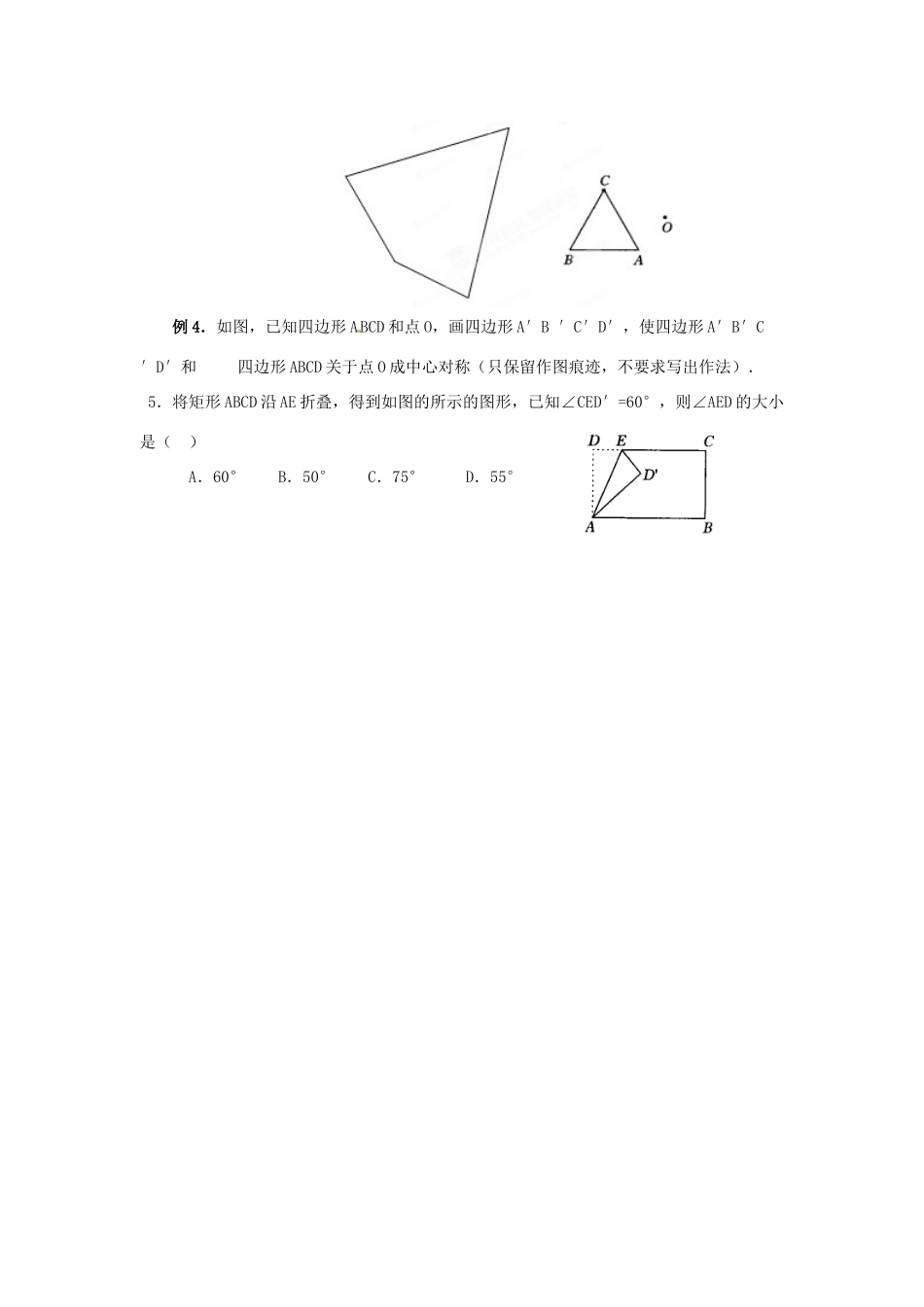
《23.2中心对称2》教案1、了解中心对称、对称中心、关于中心的对称点等概念及掌握这些概念解决一些问题.2、复习运用旋转知识作图,理解关于中心对称的两个图形,对称点所连线段都经过对称中心,而且被对称中心所平分;理解关于中心对称的两个图形是全等图形;掌握这两个性质的运用.重难点、关键1.重点:中心对称的两条基本性质及其运用.利用中心对称、对称中心、关于中心对称点的概念解决一些问题.2.难点与关键:让学生合作讨论,得出中心对称的两条基本性质.3、难点与关键:从一般旋转中导入中心对称.一、复习引入如图,△ABC绕点O旋转,使点A旋转到点D处,画出旋转后的三角形,并写出简要作法.作法:(1)(2)(3)(4)即:△DEF就是所求作的三角形,如图所示.二、探索新知问题:作出如图的两个图形绕点O旋转180°的图案,并回答下列的问题:1.以O为旋转中心,旋转180°后两个图形是否重合?2.各对称点绕O旋转180°后,这三点是否在一条直线上?定义:像这样,把一个图形___________________________,如果它能够与另一个图形重合,那么就说这两个图形关于这个点对称或中心对称,这个点叫做对称中心.这两个图形中的对应点叫做关于中心的对称点.例1.如图,四边形ABCD绕D点旋转180°,请作出旋转后的图案,写出作法并回答.(1)这两个图形是中心对称图形吗?如果是对称中心是哪一点?如果不是,请说明理由.(2)如果是中心对称,那么A、B、C、D关于中心的对称点是哪些点.解:作法:(1)(2)(3)答:(1)(2)例2.如图,已知AD是△ABC的中线,画出以点D为对称中心,与△ABD成中心对称的三角形.3.请同学任意画一三角形,以三角形一顶点为对称中心,画出这个三角形关于这个对称中心的对称图形,并分组讨论能得到什么结论.(1)作△ABC一顶点为对称中心的对称图形;(2)作关于一定点O为对称中心的对称图形.因此,我们就得到中心对称的性质:1.关于中心对称的两个图形,对称点所连线段都经过对称中心,而且被对称中心所平分.2.关于中心对称的两个图形是全等图形.例3.如图,已知△ABC和点O,画出△DEF,使△DEF和△ABC关于点O成中心对称.例4.如图,已知四边形ABCD和点O,画四边形A′B′C′D′,使四边形A′B′C′D′和四边形ABCD关于点O成中心对称(只保留作图痕迹,不要求写出作法).5.将矩形ABCD沿AE折叠,得到如图的所示的图形,已知∠CED′=60°,则∠AED的大小是()A.60°B.50°C.75°D.55°