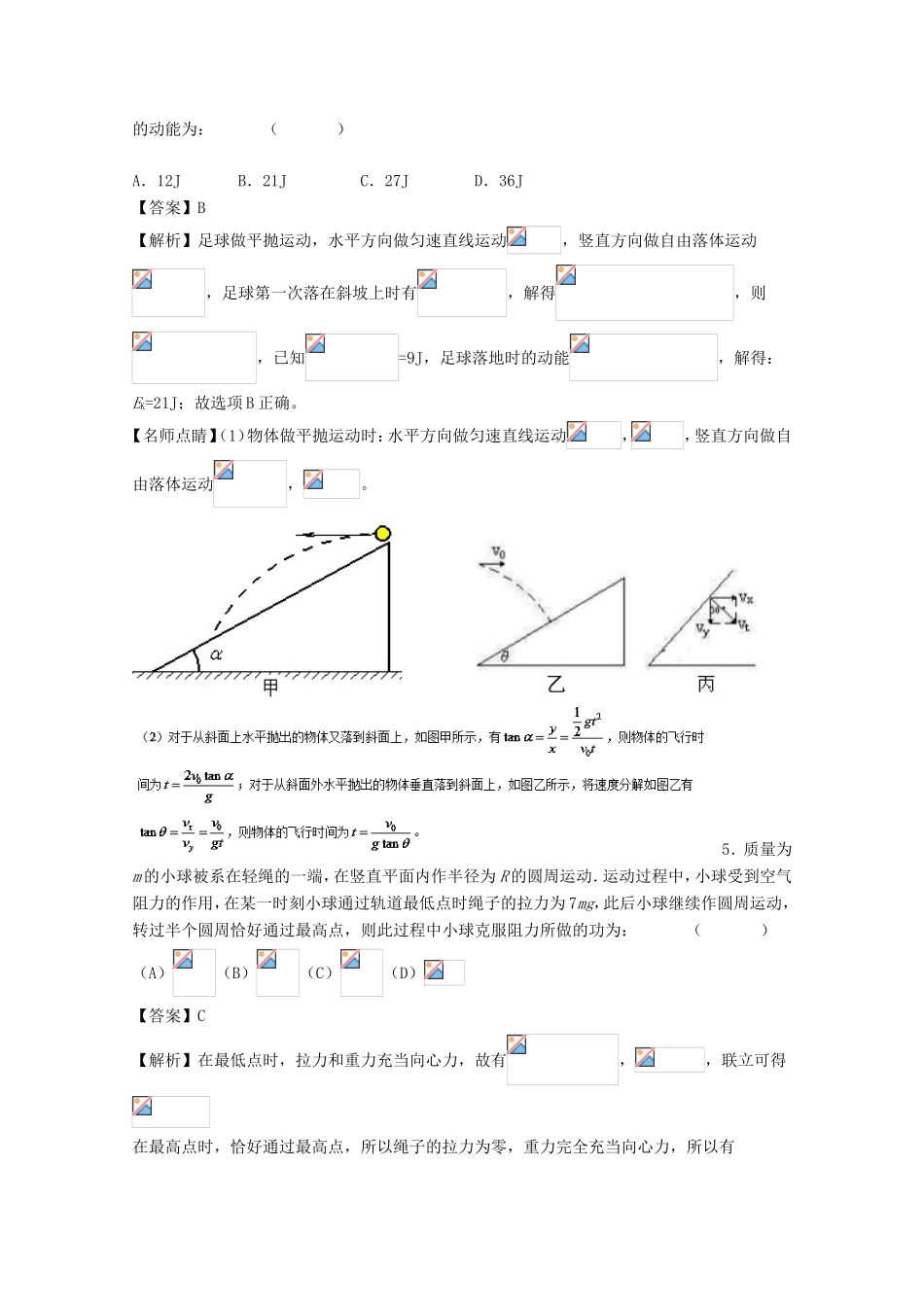
专题22应用力学两大观点分析平抛运动与圆周运动组合问题(测)【满分:110分时间:90分钟】一、选择题(本大题共12小题,每小题5分,共60分。在每小题给出的四个选项中.1~8题只有一项符合题目要求;9~12题有多项符合题目要求。全部选对的得5分,选对但不全的得3分,有选错的得0分。)1.如图所示,在地面上以速度抛出质量为m的物体,抛出后物体落到比地面低h的海平面上,若以地面为零势能面而且不计空气阻力,则①物体落到海平面时的势能为mgh②物体从抛出到落到海平面的过程红重力对物体做功为mgh③物体在海平面上的动能为④物体在海平面上的机械能为其中正确的是:()A.②③④B.①②③C.①③④D.①②④【答案】A【名师点睛】动能定理揭示了外力对物体所做总功与物体动能变化之间的关系,它描述了力在空间的积累效果,力做正功,物体的动能增加,力做负功,动能减少.动能定理解决的问题不受运动形式和受力情况的限制.还有就是重力势能的变化与零势能面的选取无关。2.以=20m/s的初速从地面竖直向上拋出一物体,上升的最大高度H=18m.设空气阻力大小不变,则上升过程和下降过程中动能和势能相等的高度分别是(以地面为重力势能零点):()A.等于9m,等于9mB.大于9m,小于9mC.小于9m,大于9mD.大于9m,大于9m【答案】B设下落过程中物体在B点处动能与势能相等,以hB表示B点的高度,vB表示物体在B点时的速度对于物体自最高点下落至B点的过程,由动能定理得:由题意有:解得:故选B.【名师点睛】本题对物体上升和下落两个过程分别运用动能定理列式,再结合条件:动能与势能相等,即可求出重力势能和动能相等的位置;运用动能定理时要灵活选取运动过程,要注意做功的正负,不能将动能和势能相等当作机械能守恒。3.质量分别为、的1、2两个小球,用长为2L的轻质杆相连,转轴在杆的中点,不计一切摩擦。初始时小球2在最高点,现让系统在竖直平面内绕固定轴O沿顺时针方向自由转动,在球1从最低点运动到最高点的过程中,下列说法正确的是:()A.运动过程中球1机械能增大B.运动过程中球2向心加速度大小不变C.球1在最高点的最小速度为零D.细杆对球1做的功为【答案】AD【名师点睛】由于两球的质量不相等,不计一切摩擦,两球做圆周运动,根据功能关系和动能定理求解即可。4.如图所示,有一个足够长的斜坡,倾角为α=30º。一个小孩在做游戏时,从该斜坡顶端将一足球沿水平方向水平踢出去,已知足球被踢出时的初动能为9J,则该足球第一次落在斜坡上时的动能为:()A.12JB.21JC.27JD.36J【答案】B【解析】足球做平抛运动,水平方向做匀速直线运动,竖直方向做自由落体运动,足球第一次落在斜坡上时有,解得,则,已知=9J,足球落地时的动能,解得:EK=21J;故选项B正确。【名师点睛】(1)物体做平抛运动时:水平方向做匀速直线运动,,竖直方向做自由落体运动,。5.质量为m的小球被系在轻绳的一端,在竖直平面内作半径为R的圆周运动.运动过程中,小球受到空气阻力的作用,在某一时刻小球通过轨道最低点时绳子的拉力为7mg,此后小球继续作圆周运动,转过半个圆周恰好通过最高点,则此过程中小球克服阻力所做的功为:()(A)(B)(C)(D)【答案】C【解析】在最低点时,拉力和重力充当向心力,故有,,联立可得在最高点时,恰好通过最高点,所以绳子的拉力为零,重力完全充当向心力,所以有,解得,从最低点到最高点过程中,重力做正功,阻力做负功,根据动能定理可得,解得,故C正确【名师点睛】在分析变力做功时,使用动能定理解题,可以省去很多麻烦,只需要明确始末速度以及哪些力做功,然后列式求解,另外注意分析用绳子拉着小球做圆周运动时,在最高点时,如果恰好能通过,则绳子的拉力为零,重力完全充当向心力。6.如图所示,一小球从斜轨道的某高度处由静止滑下,然后沿竖直光滑圆轨道的内侧运动,已知圆轨道的半径为R,忽略一切摩擦阻力,则下列说法正确的是:()A.在轨道最低点,最高点,轨道对小球作用力的方向是相同的B.小球的初位置比圆轨道最低点高出2R时,小球能通过圆轨道的最高点C.小球的初位置比圆轨道最低点高出0.5R时,小球在运动过程中不...