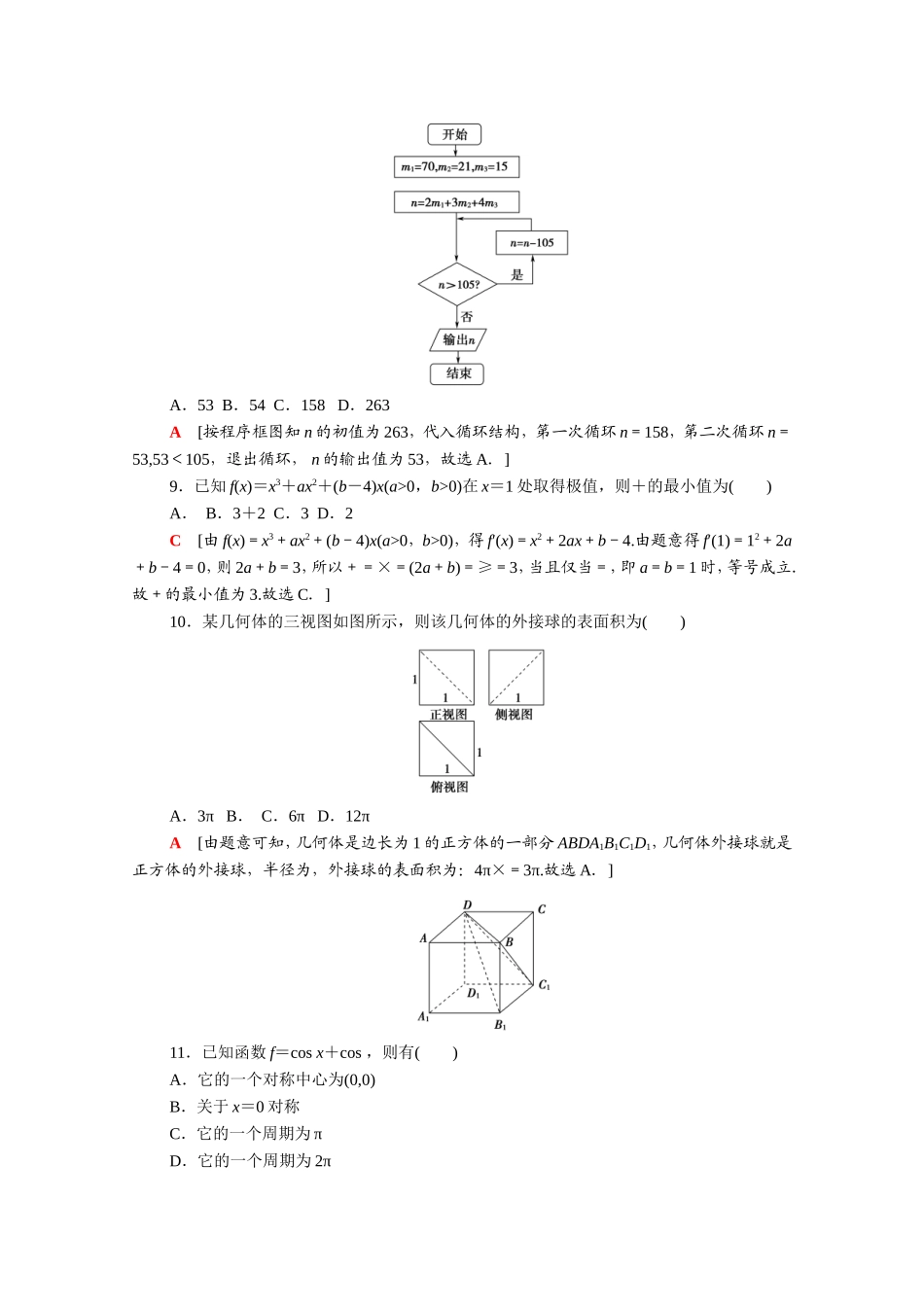
80分小题精准练(十)(建议用时:50分钟)一、选择题:本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.设全集U=R,集合A={x|-3<x<1},B={x|x+1≥0},则∁U(A∪B)=()A.{x|x≤-3或x≥1}B.{x|x<-1或x≥3}C.{x|x≤3}D.{x|x≤-3}D[因为B={x|x≥-1},A={x|-3<x<1},所以A∪B={x|x>-3},所以∁U(A∪B)={x|x≤-3}.故选D.]2.已知i是虚数单位,若z+=,则|z|=()A.1B.C.2D.B[==-i,===-i,所以=(-i)2020=i2020=i505×4=i4=1,所以由z+=,得z-i=1,z=1+i,所以|z|=.故选B.]3.如图是挪威著名画家爱德华·蒙克的作品《呐喊》的等比例缩小的图形.图中一共有3个人,仔细研究这三个人的站姿不难发现他们的脚的连线近似共线,他们的头也近似共线,这利用的相关数学知识最贴切的是()A.解析几何中的直线方程B.空间几何中的点与线的位置关系C.平面几何中的有关定理D.画法几何中的透视关系B[我们认为人与地面垂直,人之间相互平行,根据空间几何中的点与线的位置关系,可得:三个人的脚的连线近似共线,他们的头也近似共线,故选B.]4.某养猪场定购了一批仔猪,从中随机抽查了100头仔猪的体重(单位:斤),经数据处理得到如图①的频率分布直方图,其中体重最轻的14头仔猪的体重的茎叶图如图②,为了将这批仔猪分栏喂养,需计算频率分布直方图中的一些数据,其中a+b的值为()图①图②A.0.144B.0.152C.0.76D.0.076B[由题意得2(c+d)×5==0.24,∴a+b==0.152.故选B.]5.已知双曲线x2-y2=1的左右焦点为F1,F2,点A在双曲线的右支上,且AF2⊥x轴,则△AF1F2的周长为()A.4+2B.4+C.2+2D.6+2A[由题知|AF2|=1,|F1F2|=2,再由双曲线定义知|AF1|-|AF2|=2,∴|AF1|=3,所以△AF1F2的周长为4+2.]6.如图所示,在平行四边形ABCD中,点E,F分别为AD,AB的中点,且EF∩AC=H,若DH=λAD+μAB,则λ+μ=()A.B.C.D.-D[连接BD,交AC于点O,易知AH=AO,AO=AC,所以AH=AC,所以DH=DA+AH=DA+AC=-AD+AB,所以λ+μ=-.]7.已知变量x,y满足则目标函数z=x-2y的最大值为()A.-1B.1C.2D.3C[作出不等式组表示的平面区域如图阴影部分所示,由图可得,目标函数z=x-2y在点B(2,0)处取得最大值,且最大值为2.]8.(2020·衡水中学模拟)明朝数学家程大位将“孙子定理”(也称“中国剩余定理”)编成易于上口的《孙子歌诀》:三人同行七十稀,五树梅花廿一支,七子团圆正半月,除百零五便得知.已知正整数n被3除余2,被5除余3,被7除余4,求n的最小值.按此歌诀得算法如图,则输出n的结果为()A.53B.54C.158D.263A[按程序框图知n的初值为263,代入循环结构,第一次循环n=158,第二次循环n=53,53<105,退出循环,n的输出值为53,故选A.]9.已知f(x)=x3+ax2+(b-4)x(a>0,b>0)在x=1处取得极值,则+的最小值为()A.B.3+2C.3D.2C[由f(x)=x3+ax2+(b-4)x(a>0,b>0),得f′(x)=x2+2ax+b-4.由题意得f′(1)=12+2a+b-4=0,则2a+b=3,所以+=×=(2a+b)=≥=3,当且仅当=,即a=b=1时,等号成立.故+的最小值为3.故选C.]10.某几何体的三视图如图所示,则该几何体的外接球的表面积为()A.3πB.C.6πD.12πA[由题意可知,几何体是边长为1的正方体的一部分ABDA1B1C1D1,几何体外接球就是正方体的外接球,半径为,外接球的表面积为:4π×=3π.故选A.]11.已知函数f=cosx+cos,则有()A.它的一个对称中心为(0,0)B.关于x=0对称C.它的一个周期为πD.它的一个周期为2πD[对于A,因为f+f=cos+cos+cosx+cos=2cosx+2cos3cosx≠0,所以A是错误的;对于B,因为f=cos+cos=cosx+cos≠f,所以f不关于x=0对称,所以B错误;对于C,因为f=cos+cos=-cosx-cos≠f,所以C也是错误的;对于D,因为f=cos+cos(3-x+2π)=cosx+cos(3-x)=f,所以D是正确的.]12.已知函数f(x)是定义在R上的奇函数,当x<0时,f(x)=ex(x+1),给出下列命题:①当x>0时,f(x)=ex(1-x);②函数f(x)有2个零点;③f(x)>0的解集为(-1,0)∪(1,+∞);...