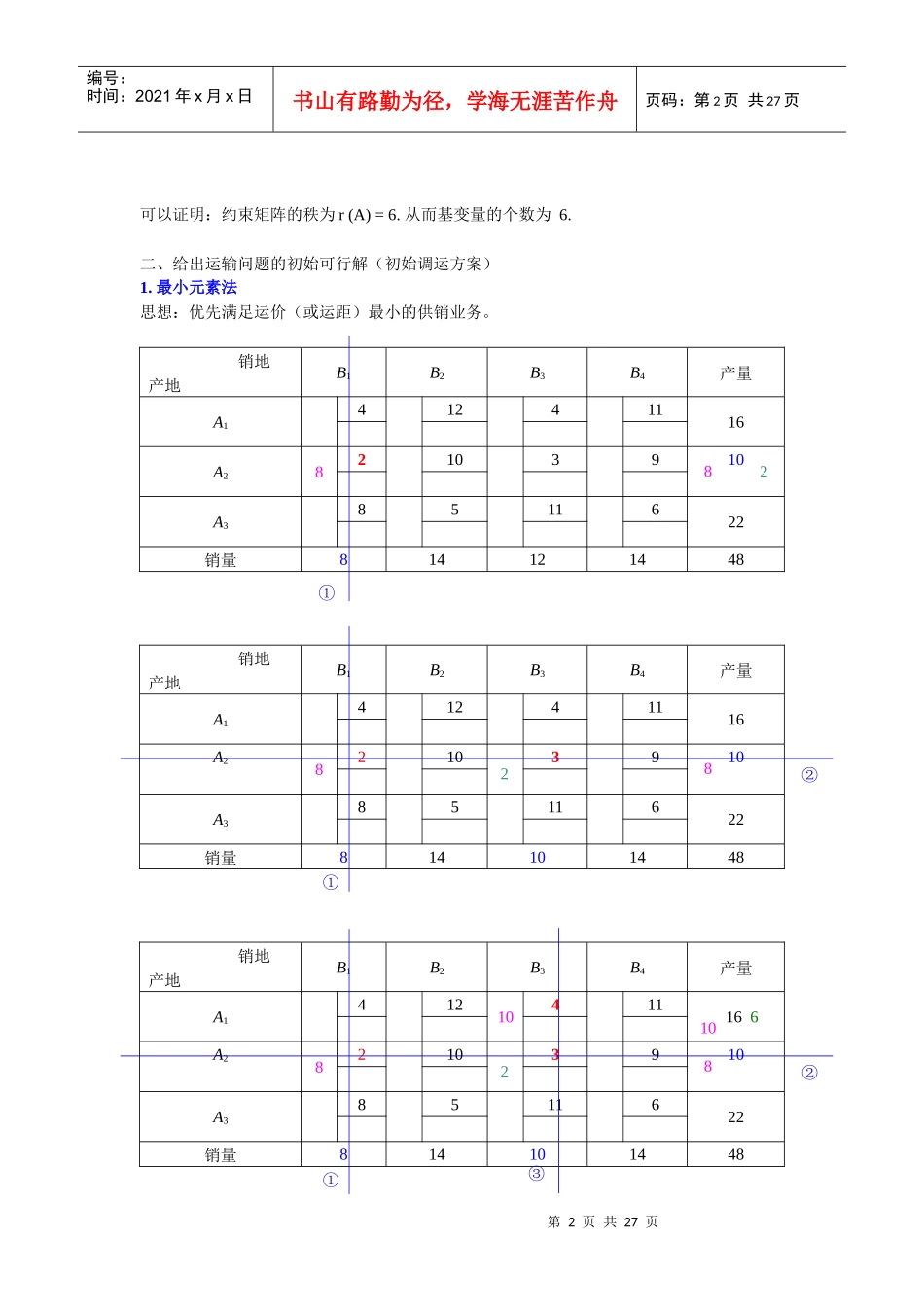
第1页共27页编号:时间:2021年x月x日书山有路勤为径,学海无涯苦作舟页码:第1页共27页P66:8.某部门有3个生产同类产品的工厂(产地),生产的产品由4个销售点出售,各工厂A1,A2,A3的生产量、各销售点B1,B2,B3,B4的销售量(假定单位为t)以及各工厂到销售点的单位运价(元/t)示于下表中,问如何调运才能使总运费最小?表销地产地B1B2B3B4产量A141241116A22103910A38511622销量814121448解:一、该运输问题的数学模型为:minz=∑i=13∑j=14cijxij=4x11+12x12+4x13+11x14+2x21+10x22+3x23+9x24+8x31+5x32+11x33+6x34{x11+x12+x13+x14¿16x21+x22+x23+x24¿10x31+x32+x33+x34¿22x11+x21+x31¿8x12+x22+x32¿14x13+x23+x33¿12x14+x24+x34¿14xij¿0,i=1,2,3;j=1,2,3,4第2页共27页第1页共27页编号:时间:2021年x月x日书山有路勤为径,学海无涯苦作舟页码:第2页共27页可以证明:约束矩阵的秩为r(A)=6.从而基变量的个数为6.二、给出运输问题的初始可行解(初始调运方案)1.最小元素法思想:优先满足运价(或运距)最小的供销业务。销地产地B1B2B3B4产量A141241116A282103910A38511622销量814121448销地产地B1B2B3B4产量A141241116A282103910A38511622销量814101448销地产地B1B2B3B4产量A141210411166A282103910A38511622销量81410144882①82②①82②①10③第3页共27页第2页共27页编号:时间:2021年x月x日书山有路勤为径,学海无涯苦作舟页码:第3页共27页销地产地B1B2B3B4产量A141210411166A282103910A38145116228销量814101448销地产地B1B2B3B4产量A141210411166A282103910A381451186220销量8141014648销地产地B1B2B3B4产量A1412104611160A2821039100A381451186220销量8141014048此时得到一个初始调运方案(初始可行解):82②①10③14④82②①10③14④⑤82②①10③14④⑤⑥⑥x34=8,x32=14,x23=2,x21=8,x14=6,x13=10,第4页共27页第3页共27页编号:时间:2021年x月x日书山有路勤为径,学海无涯苦作舟页码:第4页共27页其余(非基)变量全等于零。此解满足所有约束条件,且基变量(非零变量)的个数为6(等于m+n-1=3+4-1=6).总运费为(目标函数值)2.伏格尔(Vogel)法伏格尔法的基本思想:运输表中各行各列的最小运价与次小运价之差值(罚数)应尽可能地小。或者说:优先供应罚数最大行(或列)中最小运费的方格,以避免将运量分配到该行(或该列)次小运距的方格中。销地产地B1B2B3B4产量行差额A1412411160A221039101A385116221销量814121448列差额2513销地产地B1B2B3B4产量行差额A1412411160A221039101A38145116221→2销量814121448列差额2513销地产地B1B2B3B4产量行差额A1412411160A22103910114①80②Z=∑i=13∑j=14cijxij=10×4+6×11+8×2+2×3+14×5+8×6=246第5页共27页第4页共27页编号:时间:2021年x月x日书山有路勤为径,学海无涯苦作舟页码:第5页共27页A381451186221销量814121448列差额2513销地产地B1B2B3B4产量行差额A1412411160A28210391021A381451186221销量814121448列差额2513销地产地B1B2B3B4产量行差额A1412124111647A282103291006A381451186221销量814121448列差额2513销地产地B1B2B3B4产量行差额A14121244111607A282103291006A381451186221销量8141214048列差额251314①14①0②8③14①0②8③12④⑤14①0②8③12④⑤⑥第6页共27页第5页共27页编号:时间:2021年x月x日书山有路勤为径,学海无涯苦作舟页码:第6页共27页此时得到一个初始调运方案(初始可行解):x13=12,x14=4,x21=8,x24=2,x32=14,x34=8其余(非基)变量全等于零。此解满足所有约束条件,且基变量(非零变量)的个数为6(等于m+n-1=3+4-1=6)。总运费为(目标函数值):三、解的最优性检验⒈闭回路法(以下的闭回路都是顺时针方向)看非基变量的检验数是否满足:(1)首先对用最小元素法所确定的初始基本可行解进行检验。参见前面的计算结果,可知非基变量分别为:x11,x12,x22,x24,x31,x33。销地产地B1B2B3B4产量A1X1141210461116A2821023910A38145118622销量814121448σ11=C11+C23-(C13+C21)=4+3–(4+2)=1销地产地B1B2B3B4产量A14X121210461116A2821023910A38145118622销量814121448σ...