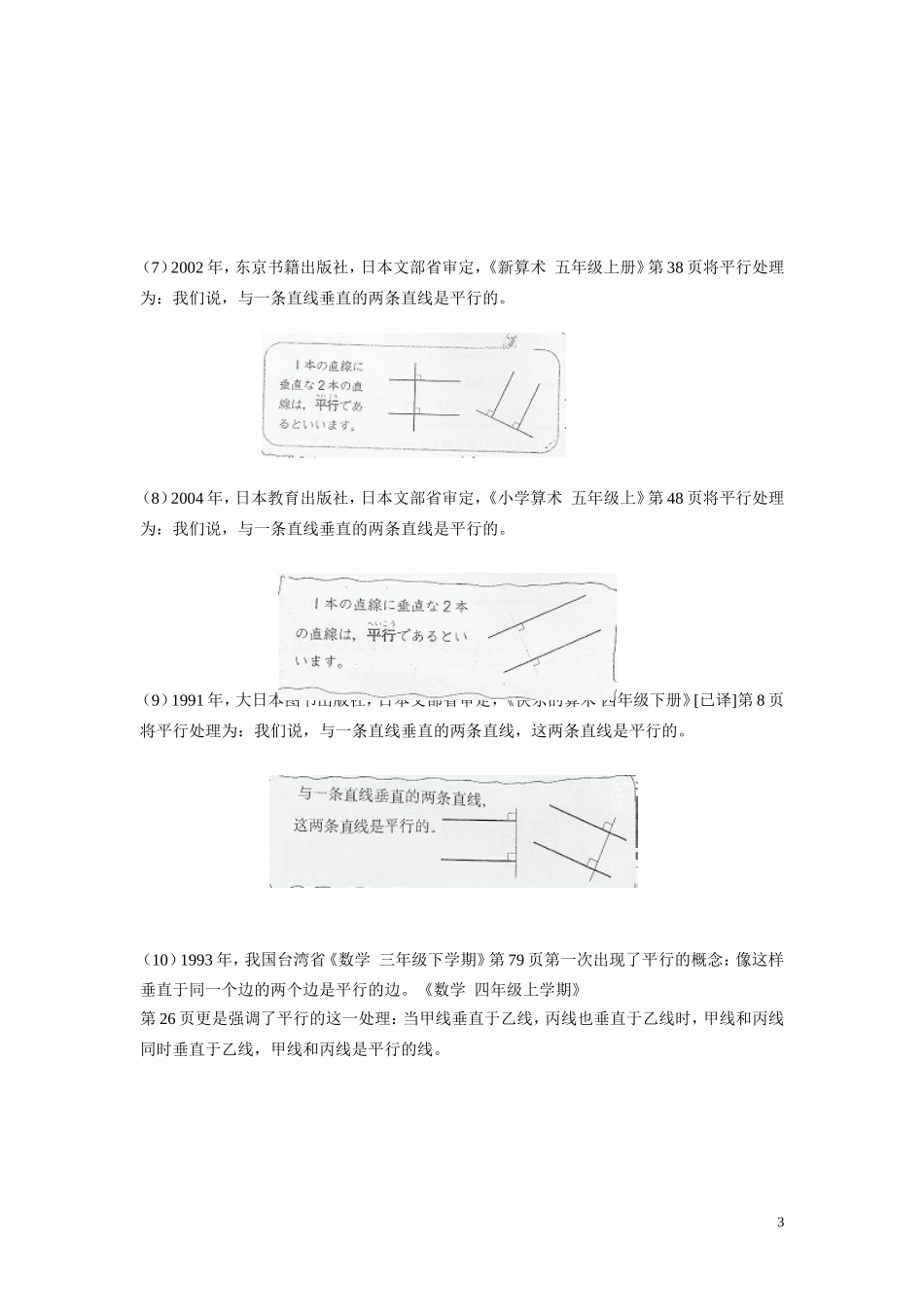
※几何的认知过程(摘自《小学数学研究》,高等教育出版社,第7、9章)第四节垂直与平行小学数学中是否出现垂直与平行的概念,世界各国的处理很不相同。在西方发达国家,垂直与平行的初次出现均在初中,亚洲某些国家与地区初次出现在小学。但只停留在线段阶段。也就是只出现线段的垂直与平行,一直要到七年级(初中)才出现直线的垂直与平行。有一点是共同的,那就是垂直与平行概念形成的标志是学生能否用尺画出垂直与平行。在教学上都是先讲线段的垂直,互相垂直的线段,直线的垂直,互相垂直的直线,然后再讲平行。按我国现行的数学课程标准,,小学、初中阶段都出现了“平行”的概念学习,小学的“平行”教学应该如何进行呢?答案是小学和初中应按照学生年龄特点对“平行”进行不同的处理。通常将平行线定义为:“在同一平面内两条不相交的直线”。这一定义对小学不大合适。原因在于,两条直线不相交,是指“无限延长”不相交,而无限延长是不能检验的。小学生面对这样不能检验的定义,无法真正把握。我们认为在小学阶段的几何学习,只有通过折叠的操作,以及实际“画”出来的直观方式感知“平行”,理解平行。于是,将平行定义为“两直线若同时垂直于第三条直线,则这两条直线互相平行”,那么这一定义是可以操作的,可以画的,可以检验的。小学生能够“画同一条直线的两条垂线”,或者“量两条直线与第三条直线的交角都是直角”。在实际生产活动中,建筑师绘图时,常常使用沿着桌边滑行的丁字尺绘制平行线就是应用这一定义。在古代,工匠们虽然没有学过数学却能画平行线,方法也是通过“两条垂直于同一直线的直线是互相平行”的活动(用角尺来画平行线)”。还有一种常用的平行线定义是:“两条直线总是有相同的距离,这两条直线是平行的。”这里使用了“距离”的概念,但“距离“的概念仍建筑在“垂直”的基础上,本质上仍然归结为“两条直线同时垂直于第三条直线”平行线定义现将我们收集到的有关“平行”定义的处理方法罗列在下面:(1)2003年,德国C.C.BuchnerKlett出版社,《Formel5MathematikfuerHauptschulen》五年级,第31页将“平行”处理为:先讲垂线,再讲距离,然后让学生通过画垂线量距离得出这两条直线之间的距离总是相等的,最后说这两条直线是平行的。1(2)2004年,Schroedel出版社,《Mathematikheute1》五年级,第144页的平行处理:先讲垂线,再讲点到直线的距离,然后再画垂直于同一直线的两条直线,再说这两条直线之间的距离总是相等的,最后说这两条直线是平行的。(3)2002年,Cornelsen出版社,《FokusMathematik5》5年级,第75页将平行处理为:垂直于同一直线的两条直线平行。(4)2000年,Schroedel出版社,《WeltderZahl》五年级,第102页将平行处理为:垂直于同一直线的两条直线平行。(5)[俄]沙雷金著,吕乃刚译,《直观几何》,华东师范大学出版社2001年1月第一版第94、95页(6)2001年,韩国大教公司《数学》四年级,第50页,将平行处理为:垂直于同一直线的两条直线平行。2(7)2002年,东京书籍出版社,日本文部省审定,《新算术五年级上册》第38页将平行处理为:我们说,与一条直线垂直的两条直线是平行的。(8)2004年,日本教育出版社,日本文部省审定,《小学算术五年级上》第48页将平行处理为:我们说,与一条直线垂直的两条直线是平行的。(9)1991年,大日本图书出版社,日本文部省审定,《快乐的算术四年级下册》[已译]第8页将平行处理为:我们说,与一条直线垂直的两条直线,这两条直线是平行的。(10)1993年,我国台湾省《数学三年级下学期》第79页第一次出现了平行的概念:像这样垂直于同一个边的两个边是平行的边。《数学四年级上学期》第26页更是强调了平行的这一处理:当甲线垂直于乙线,丙线也垂直于乙线时,甲线和丙线同时垂直于乙线,甲线和丙线是平行的线。3上海二期课改新教材关于“平行”的处理,绕过了“平面”的概念,通过“像a,b这样垂直于同一条边的两条边,我们说它们是互相平行的”,“它们之间的距离是相等的,也就是它们之间的宽是一样的,它们是互相平行的”的活动,让学生在具体操作、行为中感受、学习“...