中级质量专业理论与实务 第五讲常用分布VIP免费

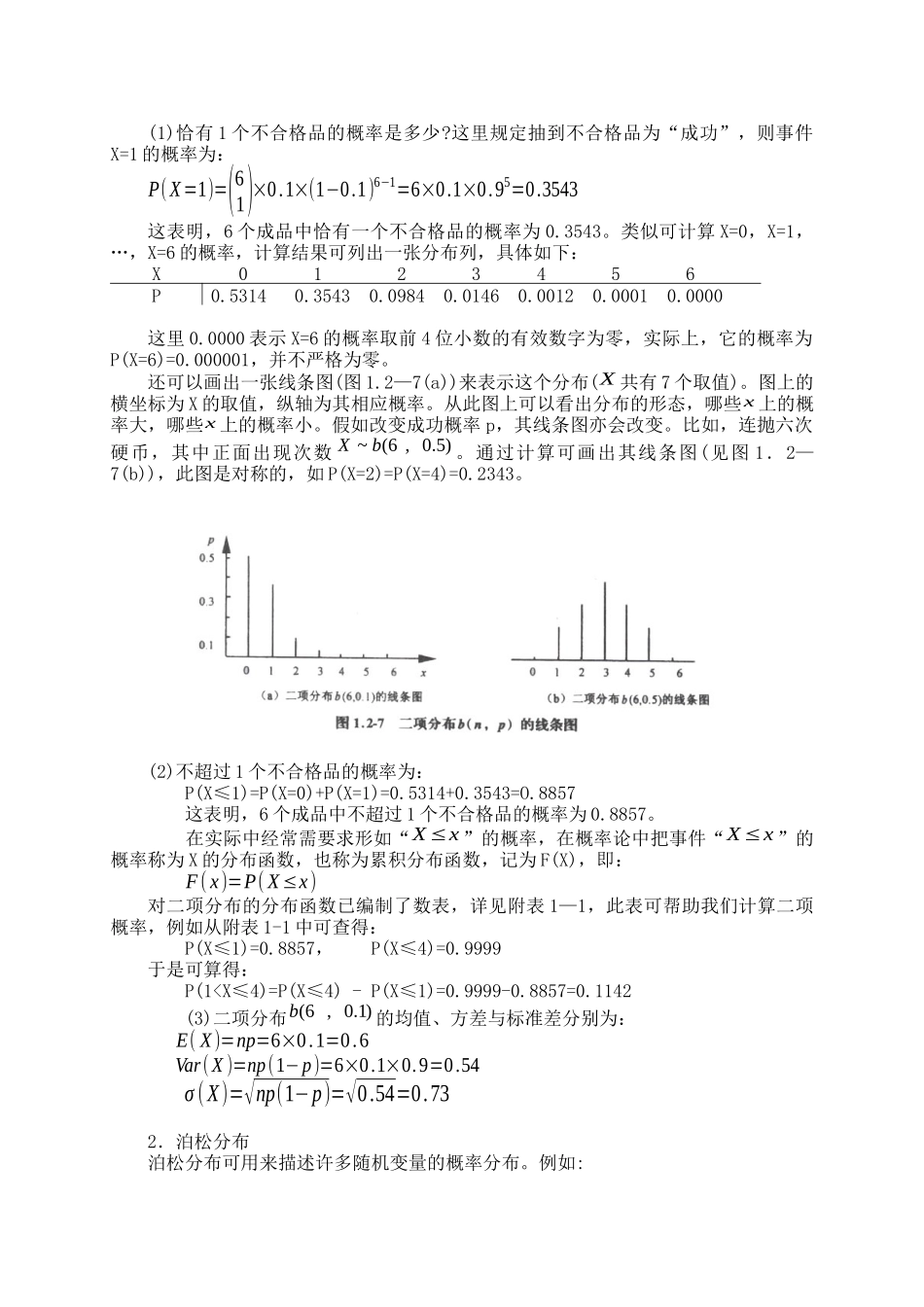
第五讲常用分布一、考试要求1.掌握二项分布、泊松分布及其均值、方差和标准差以及相关概率的计算。2.了解超几何分布。3.掌握正态分布的定义及其均值、方差和标准差，标准正态分布的分位数。4.熟悉标准正态表的用法二、内容讲解四、常用分布(一)常用离散分布这里将给出三个常用的离散分布：二项分布、泊松分布与超几何分布。1．二项分布我们来考察由n次随机试验组成的随机现象，它满足如下条件:(1)重复进行n次随机试验。比如，把一枚硬币连抛n次，检验n个产品的质量，对一个目标连续射击n次等。(2)n次试验间相互独立，即任何一次试验结果不会对其他次试验结果产生影响。(3)每次试验仅有两个可能的结果，比如，正面与反面、合格与不合格、命中与不命中、具有某特性与不具有某特性，以下统称为“成功”与“失败”。(4)每次试验成功的概率均为p，失败的概率均为1-p。在上述四个条件下，设X表示n次独立重复试验中成功出现的次数，显然X是可以取0，1，…，n等n+1个值的离散随机变量，且它的概率函数为:这个分布称为二项分布，记为，其中是从n个不同元素中取出x个的组合数，它的计算公式为：(nx)=n!x!(n−x)!二项分布的均值、方差与标准差分别为：特例：n=1的二项分布称为二点分布。它的概率函数为：或列表如下：X01P1-pp它的均值、方差与标准差分别为[例1.2-10]在—个制造过程中，不合格品率为O.1，如今从成品中随机取出6个，记X为6个成品中的不合格品数，则X服从二项分布b(6,0.1)，简记为X~b(6,0.1)。现研究如下几个问题：4)-(1.2,,1,0,)1()(nxppxnxXPxnx),(pnbxn)1()()1()()(pnpXpnpXVarnpXE1,0,)1()(1xppxXPxx)1()(,)1()(,)(ppXppXVarpXE(1)恰有1个不合格品的概率是多少?这里规定抽到不合格品为“成功”，则事件X=1的概率为：P(X=1)=(61)×0.1×(1−0.1)6−1=6×0.1×0.95=0.3543这表明，6个成品中恰有一个不合格品的概率为0.3543。类似可计算X=0，X=1，…，X=6的概率，计算结果可列出一张分布列，具体如下：X0123456P0.53140.35430.09840.01460.00120.00010.0000这里0.0000表示X=6的概率取前4位小数的有效数字为零，实际上，它的概率为P(X=6)=0.000001，并不严格为零。还可以画出一张线条图(图1.2—7(a))来表示这个分布(X共有7个取值)。图上的横坐标为X的取值，纵轴为其相应概率。从此图上可以看出分布的形态，哪些x上的概率大，哪些x上的概率小。假如改变成功概率p，其线条图亦会改变。比如，连抛六次硬币，其中正面出现次数。通过计算可画出其线条图(见图1．2—7(b))，此图是对称的，如P(X=2)=P(X=4)=0.2343。(2)不超过1个不合格品的概率为：P(X≤1)=P(X=0)+P(X=1)=0.5314+0.3543=O.8857这表明，6个成品中不超过1个不合格品的概率为0.8857。在实际中经常需要求形如“X≤x”的概率，在概率论中把事件“X≤x”的概率称为X的分布函数，也称为累积分布函数，记为F(X)，即：F(x)=P(X≤x)对二项分布的分布函数已编制了数表，详见附表1—1，此表可帮助我们计算二项概率，例如从附表1-1中可查得：P(X≤1)=0.8857，P(X≤4)=0.9999于是可算得：P(10)，又令X表示某特定单位内出现的点数，则X取x值的概率为：这个分布就称为泊松分布，记为P()，其中e为自然对数的底，即2.71828…泊松分布的均值与方差(在数量上)是相等的，均为，即：E(X)=λ，Var(X)=λ，σ(X)=√λ(1.2-6)[例1.2—11]某大公...