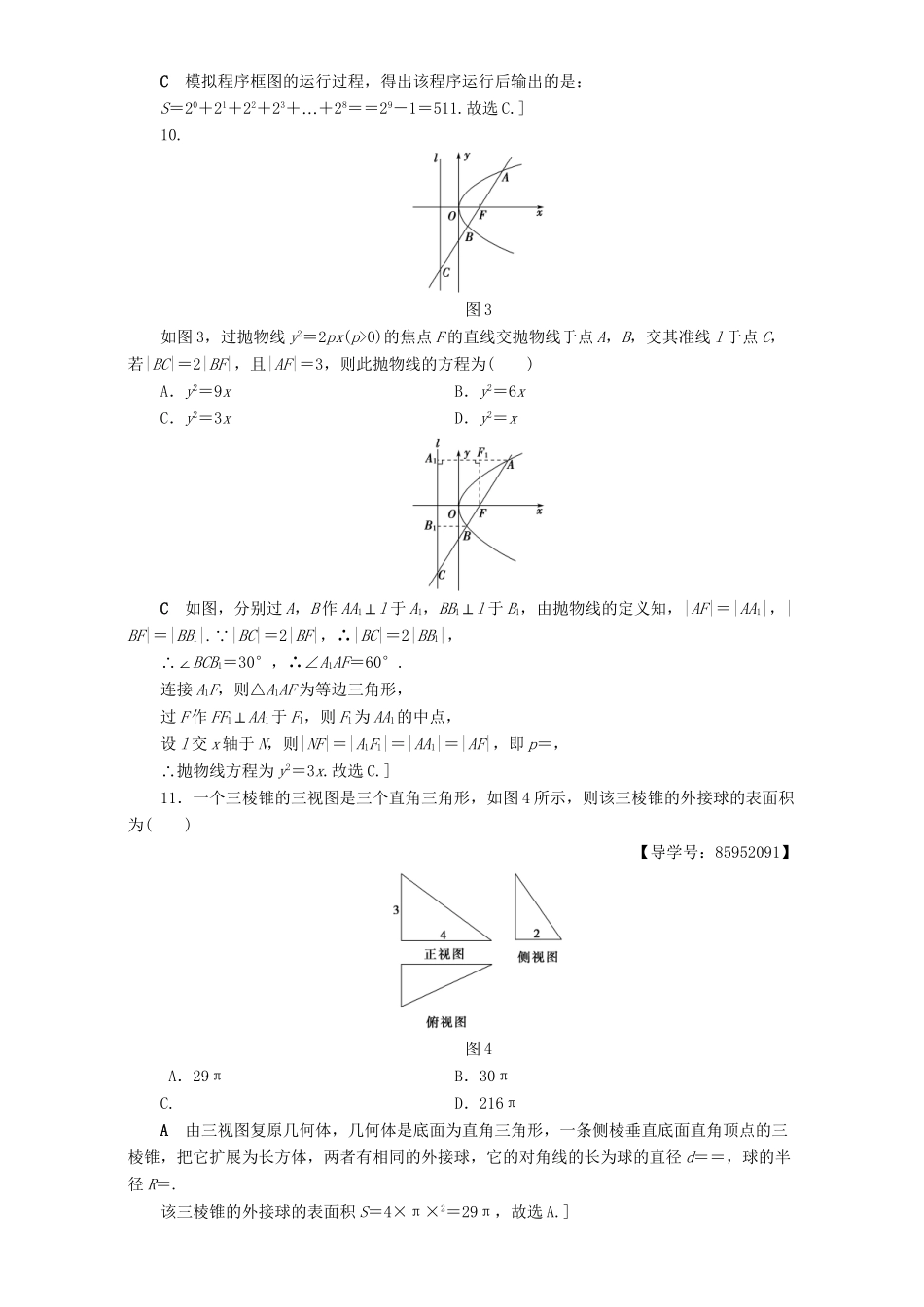
2017年高考仿真冲刺卷(一)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分,考试时间120分钟.第Ⅰ卷一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.已知集合M={x|(x+2)(x-2)≤0},N={x|x-1<0},则M∩N=()A.{x|-2≤x<1}B.{x|-2≤x≤1}C.{x|-2<x≤1}D.{x|x<-2}AM={x|(x+2)(x-2)≤0}={x|-2≤x≤2},N={x|x-1<0}={x|x<1},则M∩N={x|-2≤x<1},故选A.]2.设i是虚数单位,则复数(1-i)(1+2i)=()A.3+3iB.-1+3iC.3+iD.-1+iC复数(1-i)(1+2i)=1+2-i+2i=3+i.故选C.]3.已知函数f(x)为奇函数,且当x<0时,f(x)=2x2-1,则f(1)的值为()【导学号:85952090】A.1B.-1C.2D.-2B函数f(x)为奇函数,且当x<0时,f(x)=2x2-1,则f(1)=-f(-1)=-(2×12-1)=-1.故选B.]4.已知A,B为双曲线E的左,右顶点,点M在E上,△ABM为等腰三角形,顶角为120°,则E的离心率为()A.B.2C.D.D设M在双曲线-=1的左支上,且MA=AB=2a,∠MAB=120°,则M的坐标为(-2a,a),代入双曲线方程可得,-=1,可得a=b,c==a,即有e==.故选D.]5.(2016·黄冈模拟)若a,b∈{-1,0,1,2},则函数f(x)=ax2+2x+b有零点的概率为()A.B.C.D.A法一显然总的方法总数为16种.当a=0时,f(x)=2x+b,显然b∈{-1,0,1,2}时,原函数必有零点,所以有4种取法;当a≠0时,函数f(x)=ax2+2x+b为二次函数,若f(x)有零点须Δ≥0,即ab≤1,所以a,b取值组成的数对分别为(-1,0),(1,0),(2,0),(-1,1),(-1,-1),(1,1),(1,-1),(-1,2),(2,-1)共9种,综上符合条件的概率为=,故选A.法二(排除法)总的方法种数为16种,其中原函数若无零点须有a≠0且Δ<0,即ab>1,所以此时a,b取值组成的数对分别为:(1,2),(2,1),(2,2)共3种,所以所求有零点的概率为:1-=,故选A.]图16.在北京召开的国际数学家大会会标如图1所示,它是由4个相同的直角三角形与中间的小正方形拼成的一大正方形.若直角三角形中较小的锐角为θ,大正方形的面积是1,小正方形的面积是,则sin2θ-cos2θ的值等于()A.1B.-C.D.-B依题意可知拼图中的每个直角三角形的长直角边为cosθ,短直角边为sinθ,小正方形的边长为cosθ-sinθ. 小正方形的面积是,∴(cosθ-sinθ)2=.又θ为直角三角形中较小的锐角,∴cosθ>sinθ,∴cosθ-sinθ=.又 (cosθ-sinθ)2=1-2sinθcosθ=,∴2cosθsinθ=,∴1+2sinθcosθ=,即(cosθ+sinθ)2=,∴cosθ+sinθ=,∴sin2θ-cos2θ=(cosθ+sinθ)(sinθ-cosθ)=-×=-,故选B.]7.已知向量a=(cosα,-2),b=(sinα,1),且a∥b,则tan等于()A.3B.-3C.D.-B a∥b,∴cosα+2sinα=0,∴tanα=-,∴tan==-3,故选B.]8.下面命题中假命题是()A.∀x∈R,3x>0B.∃α,β∈R,使sin(α+β)=sinα+sinβC.∃m∈R,使f(x)=mxm2+2是幂函数,且在(0∞,+)上单调递增D“.命题∃x∈R,x2+1>3x”“的否定是∀x∈R,x2+1>3x”D对于A,根据指数函数的性质可知,∀x∈R,3x>0,∴A正确.对于B,当α=β=0时,满足sin(α+β)=sinα+sinβ=0,∴B正确.对于C,当m=1时,幂函数为f(x)=x3,且在(0∞,+)上单调递增,∴C正确.对于D“,命题∃x∈R,x2+1>3x”“的否定是∀x∈R,x2+1≤3x”,∴D错误.故选D.]9.执行如图2所示的程序框图,则输出的S=()图2A.1023B.512C.511D.255C模拟程序框图的运行过程,得出该程序运行后输出的是:S=20+21+22+23…++28==29-1=511.故选C.]10.图3如图3,过抛物线y2=2px(p>0)的焦点F的直线交抛物线于点A,B,交其准线l于点C,若|BC|=2|BF|,且|AF|=3,则此抛物线的方程为()A.y2=9xB.y2=6xC.y2=3xD.y2=xC如图,分别过A,B作AA1⊥l于A1,BB1⊥l于B1,由抛物线的定义知,|AF|=|AA1|,|BF|=|BB1|. |BC|=2|BF|,∴|BC|=2|BB1|,∴∠BCB1=30°,∴∠A1AF=60°.连接A1F,则△A1AF为等边三角形,过F作FF1⊥AA1于F1,则F1为AA1的中点,设l交x轴于N,则|NF|=|A1F1|=|AA1|...