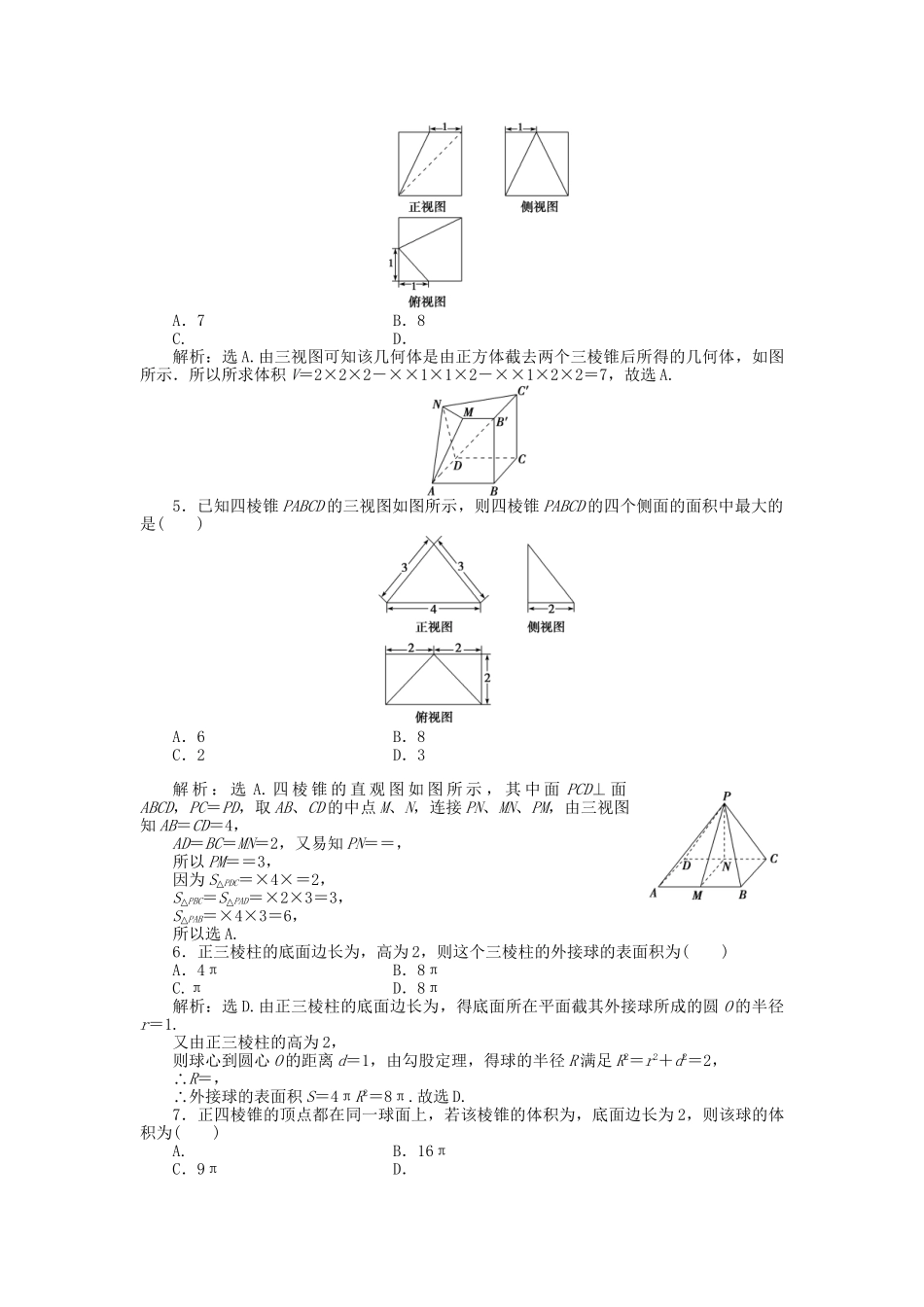
(通用版)2016年高考数学二轮复习专题八立体几何第1讲三视图与几何体的面积与体积专题强化训练理(时间:45分钟满分:60分)一、选择题1.如图所示为一个简单几何体的三视图,则其对应的几何体是()解析:选A.对于A,该几何体的三视图恰好与已知图形相符,故A符合题意;对于B,该几何体的正视图中,对角线应该是虚线,故不符合题意;对于C,该几何体的正视图的矩形中,对角线应该是从左上到右下的方向,故不符合题意;对于D,该几何体的侧视图的矩形中,对角线应该是虚线,且是从右上到左下的方向,故不符合题意,故选A.2.将长方体截去一个四棱锥,得到的几何体如图所示,则该几何体的侧视图是()解析:选D.由几何体可以看出,侧视图应为一个矩形外加一条从右上到左下的对角线,故选D.3.如图所示是某一几何体的三视图,则它的体积为()A.32+12πB.64+12πC.36+12πD.64+16π解析:选B.由三视图知,该几何体是圆柱与正四棱锥的组合体,圆柱的高为3,底面直径为4,∴圆柱的体积为π×22×3=12π;正四棱锥的高为3,侧面上的斜高为5,∴正四棱锥的底面边长为2×=8,∴四棱锥的体积为×82×3=64,故几何体的体积V=64+12π.故选B.4.某几何体的三视图(图中正方形的边长为2)如图所示,则该几何体的体积为()A.7B.8C.D.解析:选A.由三视图可知该几何体是由正方体截去两个三棱锥后所得的几何体,如图所示.所以所求体积V=2×2×2-××1×1×2-××1×2×2=7,故选A.5.已知四棱锥PABCD的三视图如图所示,则四棱锥PABCD的四个侧面的面积中最大的是()A.6B.8C.2D.3解析:选A.四棱锥的直观图如图所示,其中面PCD⊥面ABCD,PC=PD,取AB、CD的中点M、N,连接PN、MN、PM,由三视图知AB=CD=4,AD=BC=MN=2,又易知PN==,所以PM==3,因为S△PDC=×4×=2,S△PBC=S△PAD=×2×3=3,S△PAB=×4×3=6,所以选A.6.正三棱柱的底面边长为,高为2,则这个三棱柱的外接球的表面积为()A.4πB.8πC.πD.8π解析:选D.由正三棱柱的底面边长为,得底面所在平面截其外接球所成的圆O的半径r=1.又由正三棱柱的高为2,则球心到圆心O的距离d=1,由勾股定理,得球的半径R满足R2=r2+d2=2,∴R=,∴外接球的表面积S=4πR2=8π.故选D.7.正四棱锥的顶点都在同一球面上,若该棱锥的体积为,底面边长为2,则该球的体积为()A.B.16πC.9πD.解析:选A.如图,O为球心,O1为点P在平面ABCD上的射影,连接PO1,AO,AC.由题意知=×2×2×PO1,则PO1=4.设球的半径为R, PO1=4,底面边长为2,∴R2=(4-R)2+()2,∴R=,∴球的体积为=.故选A.8.一个三棱锥的三条侧棱OA、OB、OC两两互相垂直,且OA=3、OB=4、OC=2,则该三棱锥的外接球的表面积为()A.29πB.30πC.D.216解析:选A.把三棱锥补形为一个长、宽、高分别为3、2、4的长方体,则长方体和三棱锥有相同的外接球,长方体的对角线长为球的直径,即2R==(R为球的半径),球的半径为.故该三棱锥的外接球的表面积为4×π×()2=29π,选A.9.已知正四面体ABCD,点E、F分别为棱AB、AC的中点,球O是正四面体ABCD的外接球,球O截直线EF所得弦长为6,则正四面体的棱长为()A.6B.12C.6D.6解析:选B.如图,将正四面体补成正方体,设正四面体的棱长为2a,则正方体的棱长为a,正方体的体对角线长为a,正四面体的外接球的半径为.设球心为O,O到EF的距离为d,则d===a,所以球O截直线EF所得弦长为2=6.解得a=6,所以正四面体的棱长为12.故选B.10.已知半径为5的球O被互相垂直的两个平面所截,得到的两个圆的公共弦为4,若其中的一圆的半径为4,则另一圆的半径为()A.3B.2C.4D.解析:选D.如图,设两圆的圆心分别为O1、O2,球心为O,公共弦为AB,其中点为E,连接OO1、O1E、EO2、O2O、OE、O1O2、OA、O1A,则四边形OO1EO2为矩形,O1O2=OE===.设圆O1的半径为4,则O1E===2,∴O2E==3,∴圆O2的半径为=.故选D.11.在长方体ABCDA1B1C1D1中,AB=BC=2,过A1,C1,B三点的平面截去长方体的一个角后,得到如图所示的几何体ABCDA1C1D1,这个几何体的体积为,则经过A1,C1,B,D四点的球的表面积为()A.36πB.24πC.12π...