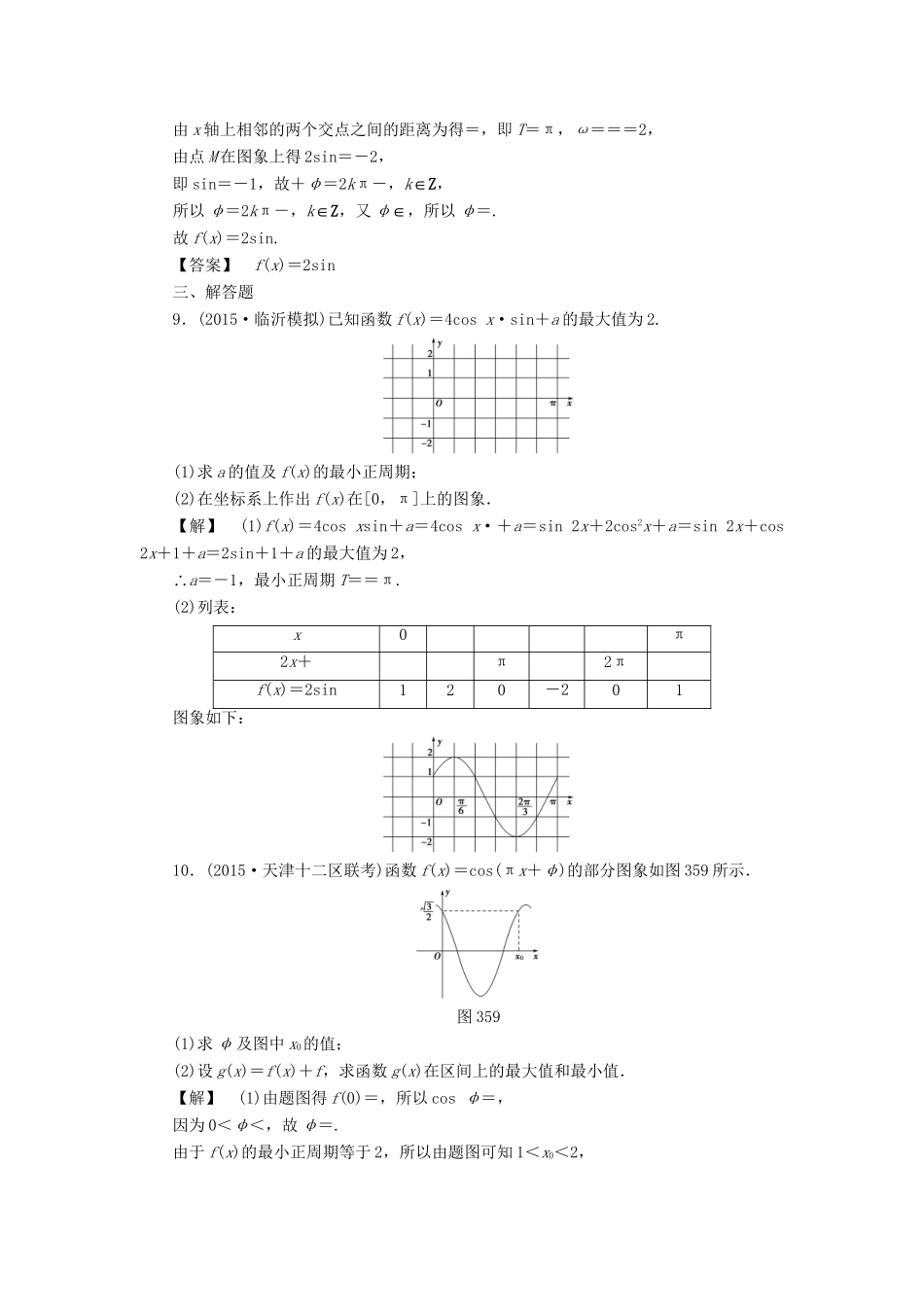
分层限时跟踪练(二十一)(限时40分钟)一、选择题1.(2014·浙江高考)为了得到函数y=sin3x+cos3x的图象,可以将函数y=cos3x的图象()A.向右平移个单位B.向左平移个单位C.向右平移个单位D.向左平移个单位【解析】因为y=sin3x+cos3x=sin=sin,又y=cos3x=sin=sin,所以应由y=cos3x的图象向右平移个单位得到.【答案】C2.(2015·陕西高考)如图357,某港口一天6时到18时的水深变化曲线近似满足函数y=3sin+k.据此函数可知,这段时间水深(单位:m)的最大值为()图357A.5B.6C.8D.10【解析】分析三角函数图象,根据最小值求k,再求最大值.根据图象得函数的最小值为2,有-3+k=2,k=5,最大值为3+k=8.【答案】C3.(2015·济南模拟)将函数y=cos2x的图象向左平移个单位,得到函数y=f(x)·cosx的图象,则f(x)的表达式可以是()A.f(x)=-2sinxB.f(x)=2sinxC.f(x)=sin2xD.f(x)=(sin2x+cos2x)【解析】将函数y=cos2x的图象向左平移个单位,得到函数y=cos=cos=-sin2x的图象,因为-sin2x=-2sinxcosx,所以f(x)=-2sinx.【答案】A4.(2015·太原模拟)已知函数f(x)=sin(ωx+φ)的最小正周期是π,若将f(x)的图象向右平移个单位后得到的图象关于原点对称,则函数f(x)的图象()A.关于直线x=对称B.关于直线x=对称C.关于点对称D.关于点对称【解析】 f(x)的最小正周期为π,∴=π,ω=2,∴f(x)的图象向右平移个单位后得到g(x)=sin=sin的图象,又g(x)的图象关于原点对称,∴-+φ=kπ,k∈Z,∴φ=+kπ,k∈Z,又|φ|<,∴<,∴k=-1,φ=-,∴f(x)=sin.当x=时,2x-=-.∴A、C错误;当x=时,2x-=,∴B正确,D错误.【答案】B5.(2015·湖南高考)将函数f(x)=sin2x的图象向右平移φ个单位后得到函数g(x)的图象.若对满足|f(x1)-g(x2)|=2的x1,x2,有|x1-x2|min=,则φ=()A.B.C.D.【解析】因为g(x)=sin2(x-φ)=sin(2x-2φ),所以|f(x1)-g(x2)|=|sin2x1-sin(2x2-2φ)|=2.因为-1≤sin2x1≤1,-1≤sin(2x2-2φ)≤1,所以sin2x1和sin(2x2-2φ)的值中,一个为1,另一个为-1,不妨取sin2x1=1,sin(2x2-2φ)=-1,则2x1=2k1π+,k1∈Z,2x2-2φ=2k2π-,k2∈Z,2x1-2x2+2φ=2(k1-k2)π+π,(k1-k2)∈Z,得|x1-x2|=.因为0<φ<,所以0<-φ<,故当k1-k2=0时,|x1-x2|min=-φ=,则φ=,故选D.【答案】D二、填空题6.(2014·重庆高考)将函数f(x)=sin(ωx+φ)图象上每一点的横坐标缩短为原来的一半,纵坐标不变,再向右平移个单位长度得到y=sinx的图象,则f=.【解析】将y=sinx的图象向左平移个单位长度可得y=sin的图象,保持纵坐标不变,横坐标变为原来的2倍可得y=sin的图象,故f(x)=sin.所以f=sin=sin=.【答案】图3587.(2015·扬州模拟)已知函数f(x)=Asin(ωx+φ)A>0,ω>0,0<φ<的部分图象如图358所示.当x∈时,函数y=f(x-1)+f(x)的值域为.【解析】由题图得,A=2,=-=1,得T=4,ω=,则f(x)=2sin.由f=2sin=2,得sin=1,所以+φ=2kπ+(k∈Z),又0<φ<,得φ=,所以f(x)=2sin,y=f(x-1)+f(x)=2sin-2cos=2sin.因为x∈,故≤x≤-,则≤-sin≤1,即≤-y≤2,所以函数y=f(x-1)+f(x)的值域为[-,2].【答案】[-,2]8.已知函数f(x)=Asin(ωx+φ)其中A>0,ω>0,0<φ<的图象与x轴的交点中,相邻两个交点之间的距离为,且图象上一个最低点为M,则f(x)的解析式为.【解析】由最低点为M得A=2.由x轴上相邻的两个交点之间的距离为得=,即T=π,ω===2,由点M在图象上得2sin=-2,即sin=-1,故+φ=2kπ-,k∈Z,所以φ=2kπ-,k∈Z,又φ∈,所以φ=.故f(x)=2sin.【答案】f(x)=2sin三、解答题9.(2015·临沂模拟)已知函数f(x)=4cosx·sin+a的最大值为2.(1)求a的值及f(x)的最小正周期;(2)在坐标系上作出f(x)在[0,π]上的图象.【解】(1)f(x)=4cosxsin+a=4cosx·+a=sin2x+2cos2x+a=sin2x+cos2x+1+a=2sin+1+a的最大值为2,∴a=-1,最小正周期T==π.(2)列表:x0π2x+π2πf(x)=2sin120-201图象如下:10.(2015·天...