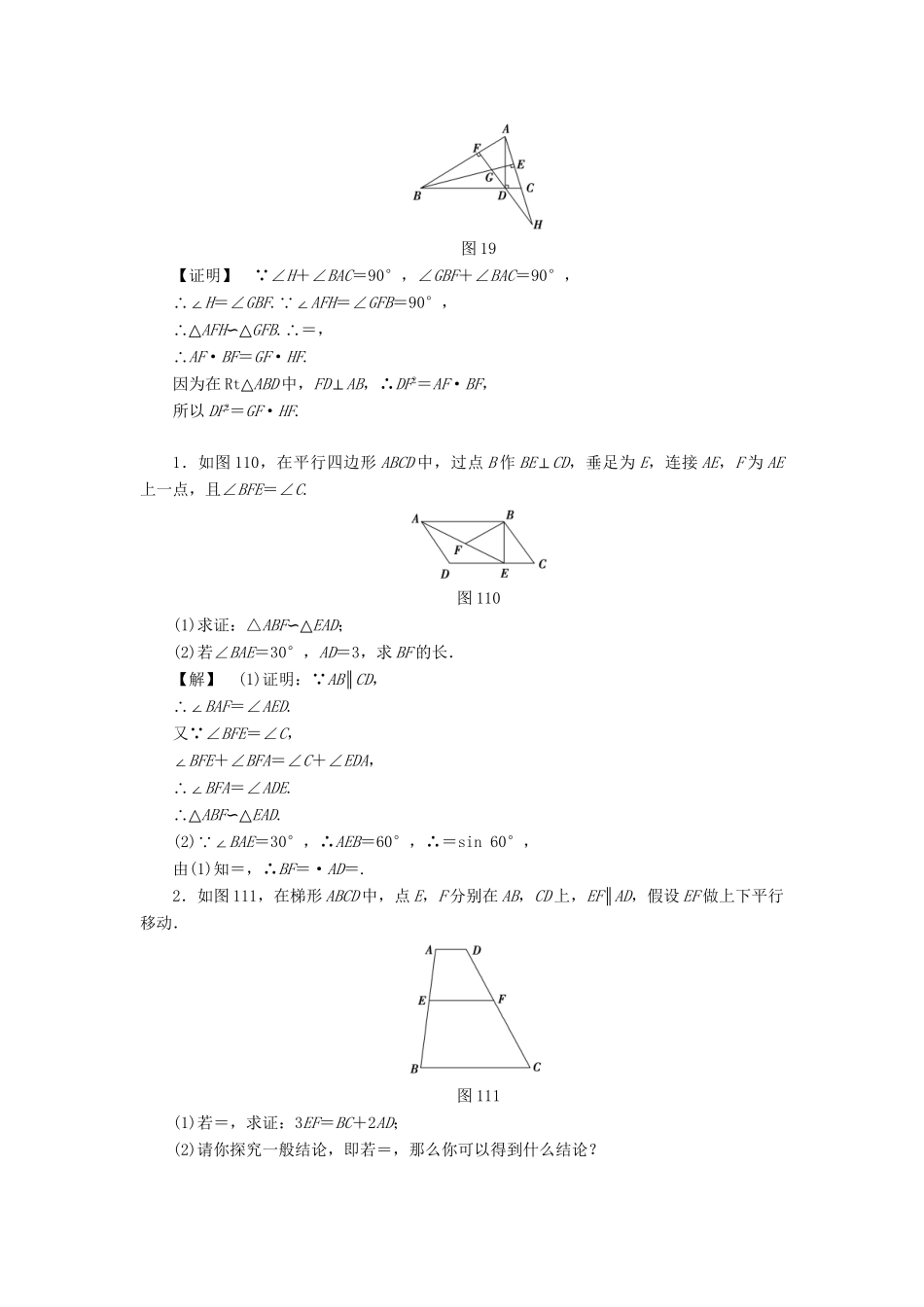
跟踪演练(一)(建议用时:40分)1.如图17,在△ABC中,点D是AC的中点,点E是BD的中点,AE交BC于点F,求的值.图17【解】如图,过点D作DM∥AF交BC于点M.因为点E是BD的中点,所以在△BDM中,BF=FM.又点D是AC的中点,所以在△CAF中,CM=MF,所以==.2.(2015·江苏高考)如图18,在△ABC中,AB=AC,△ABC的外接圆⊙O的弦AE交BC于点D.图18求证:△ABD∽△AEB.【证明】因为AB=AC,所以∠ABD=∠C.又因为∠C=∠E,所以∠ABD=∠E.又∠BAE为公共角,所以△ABD∽△AEB.3.如图19所示,AD,BE是△ABC的两条高,DF⊥AB,垂足为F,直线FD交BE于点G,交AC的延长线于H,求证:DF2=GF·HF.图19【证明】∵∠H+∠BAC=90°,∠GBF+∠BAC=90°,∴∠H=∠GBF.∵∠AFH=∠GFB=90°,∴△AFH∽△GFB.∴=,∴AF·BF=GF·HF.因为在Rt△ABD中,FD⊥AB,∴DF2=AF·BF,所以DF2=GF·HF.1.如图110,在平行四边形ABCD中,过点B作BE⊥CD,垂足为E,连接AE,F为AE上一点,且∠BFE=∠C.图110(1)求证:△ABF∽△EAD;(2)若∠BAE=30°,AD=3,求BF的长.【解】(1)证明:∵AB∥CD,∴∠BAF=∠AED.又∵∠BFE=∠C,∠BFE+∠BFA=∠C+∠EDA,∴∠BFA=∠ADE.∴△ABF∽△EAD.(2)∵∠BAE=30°,∴AEB=60°,∴=sin60°,由(1)知=,∴BF=·AD=.2.如图111,在梯形ABCD中,点E,F分别在AB,CD上,EF∥AD,假设EF做上下平行移动.图111(1)若=,求证:3EF=BC+2AD;(2)请你探究一般结论,即若=,那么你可以得到什么结论?【解】过点A作AH∥CD分别交EF,BC于点G,H.(1)证明:因为=,所以=.又EG∥BH,所以==,即3EG=BH.又EG+GF=EG+AD=EF,从而EF=(BC-HC)+AD,所以EF=BC+AD,即3EF=BC+2AD.(2)因为=,所以=.又EG∥BH,所以=,即EG=BH.所以EF=EG+GF=EG+AD=(BC-AD)+AD,所以EF=BC+AD,即(m+n)EF=mBC+nAD.