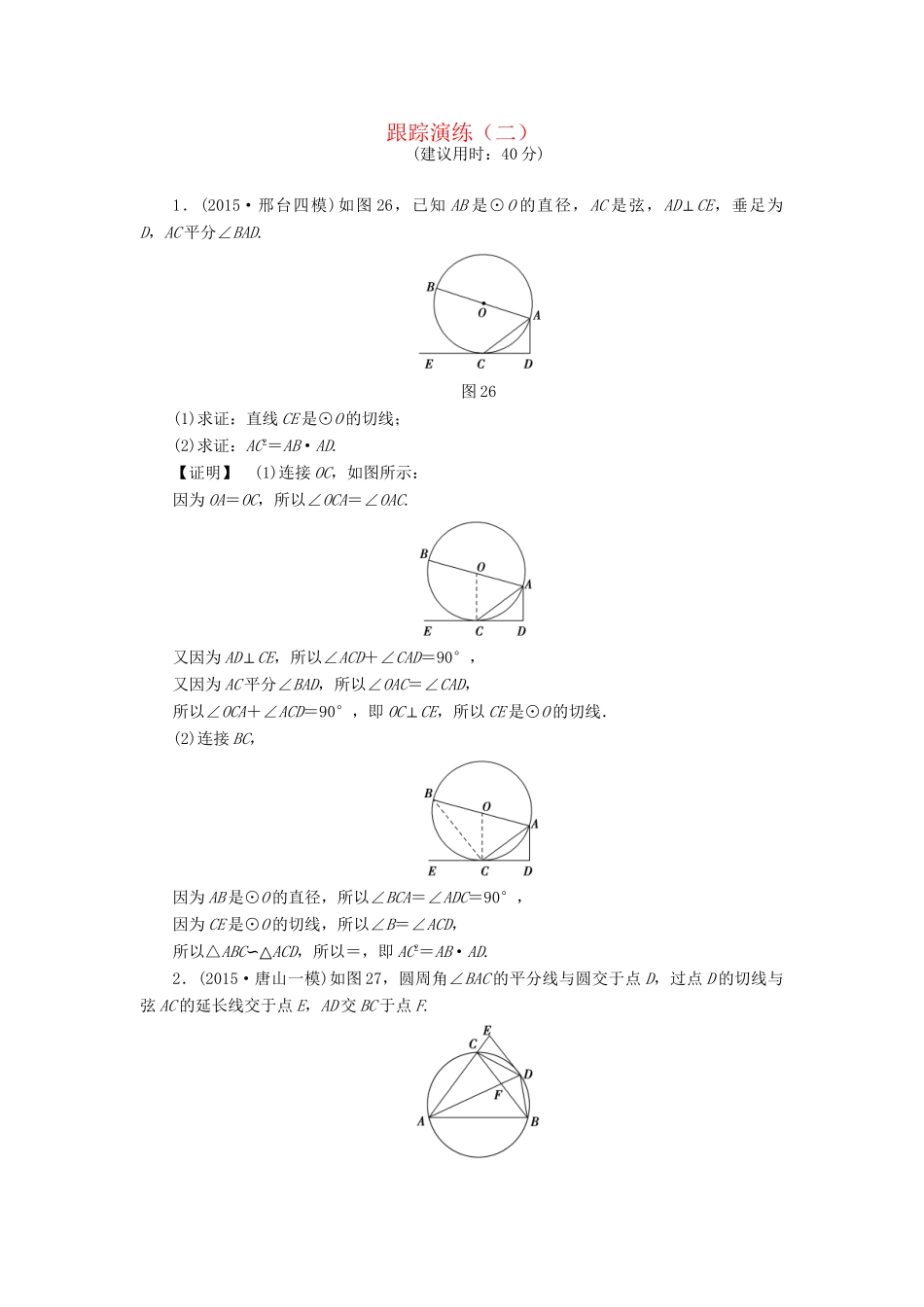
跟踪演练(二)(建议用时:40分)1.(2015·邢台四模)如图26,已知AB是⊙O的直径,AC是弦,AD⊥CE,垂足为D,AC平分∠BAD.图26(1)求证:直线CE是⊙O的切线;(2)求证:AC2=AB·AD.【证明】(1)连接OC,如图所示:因为OA=OC,所以∠OCA=∠OAC.又因为AD⊥CE,所以∠ACD+∠CAD=90°,又因为AC平分∠BAD,所以∠OAC=∠CAD,所以∠OCA+∠ACD=90°,即OC⊥CE,所以CE是⊙O的切线.(2)连接BC,因为AB是⊙O的直径,所以∠BCA=∠ADC=90°,因为CE是⊙O的切线,所以∠B=∠ACD,所以△ABC∽△ACD,所以=,即AC2=AB·AD.2.(2015·唐山一模)如图27,圆周角∠BAC的平分线与圆交于点D,过点D的切线与弦AC的延长线交于点E,AD交BC于点F.图27(1)求证:BC∥DE;(2)若D,E,C,F四点共圆,且=,求∠BAC.【解】(1)因为∠EDC=∠DAC,∠DAC=∠DAB,∠DAB=∠DCB,所以∠EDC=∠DCB,所以BC∥DE.(2)因为D,E,C,F四点共圆,所以∠CFA=∠CED,由(1)知∠ACF=∠CED,所以∠CFA=∠ACF.设∠DAC=∠DAB=x,因为=,所以∠CBA=∠BAC=2x,所以∠CFA=∠FBA+∠FAB=3x,在等腰三角形ACF中,π=∠CFA+∠ACF+∠CAF=7x,则x=,所以∠BAC=2x=.1.(2015·郑州二模)如图28,⊙O是△ABC的外接圆,∠BAC的平分线交BC于点F,D是AF的延长线与⊙O的交点,AC的延长线与⊙O的切线DE交于点E.图28(1)求证:=;(2)若BD=3,EC=2,CA=6,求BF的值.【解】(1)证明:连接CD,∵AD是∠BAC的平分线,∴∠BAD=∠EAD,又∵DE与⊙O相切于D,∴∠CDE=∠EAD=∠BAD,∵∠DCE是⊙O的内接四边形ABDC的外角,∴∠DCE=∠ABD,∴△DCE∽△ABD,∴=.(2)∵AD是∠BAC的平分线,∴=,∴BD=CD=3,∠CBD=∠BCD,∵DE与⊙O相切于D,EC=2,CA=6,∴DE2=EC·EA=EC·(EC+CA)=16,∠CDE=∠CBD,∴DE=4,∠CDE=∠BCD,∴DE∥BC,∴∠E=∠ACB=∠ADB,∴△DCE∽△BFD,∴=,∴BF==.2.(2015·全国卷Ⅱ)如图29,O为等腰三角形ABC内一点,⊙O与△ABC的底边BC交于M,N两点,与底边上的高AD交于点G,且与AB,AC分别相切于E,F两点.(1)证明:EF∥BC;(2)若AG等于⊙O的半径,且AE=MN=2,求四边形EBCF的面积.【解】(1)证明:由于△ABC是等腰三角形,AD⊥BC,所以AD是∠CAB的平分线.又因为⊙O分别与AB,AC相切于点E,F,所以AE=AF,故AD⊥EF,从而EF∥BC.(2)由(1)知,AE=AF,AD⊥EF,故AD是EF的垂直平分线.又EF为⊙O的弦,所以O在AD上.连接OE,OM,则OE⊥AE.由AG等于⊙O的半径得AO=2OE,所以∠OAE=30°.因此△ABC和△AEF都是等边三角形.因为AE=2,所以AO=4,OE=2.因为OM=OE=2,DM=MN=,所以OD=1.于是AD=5,AB=.所以四边形EBCF的面积为×2×-×(2)2×=.