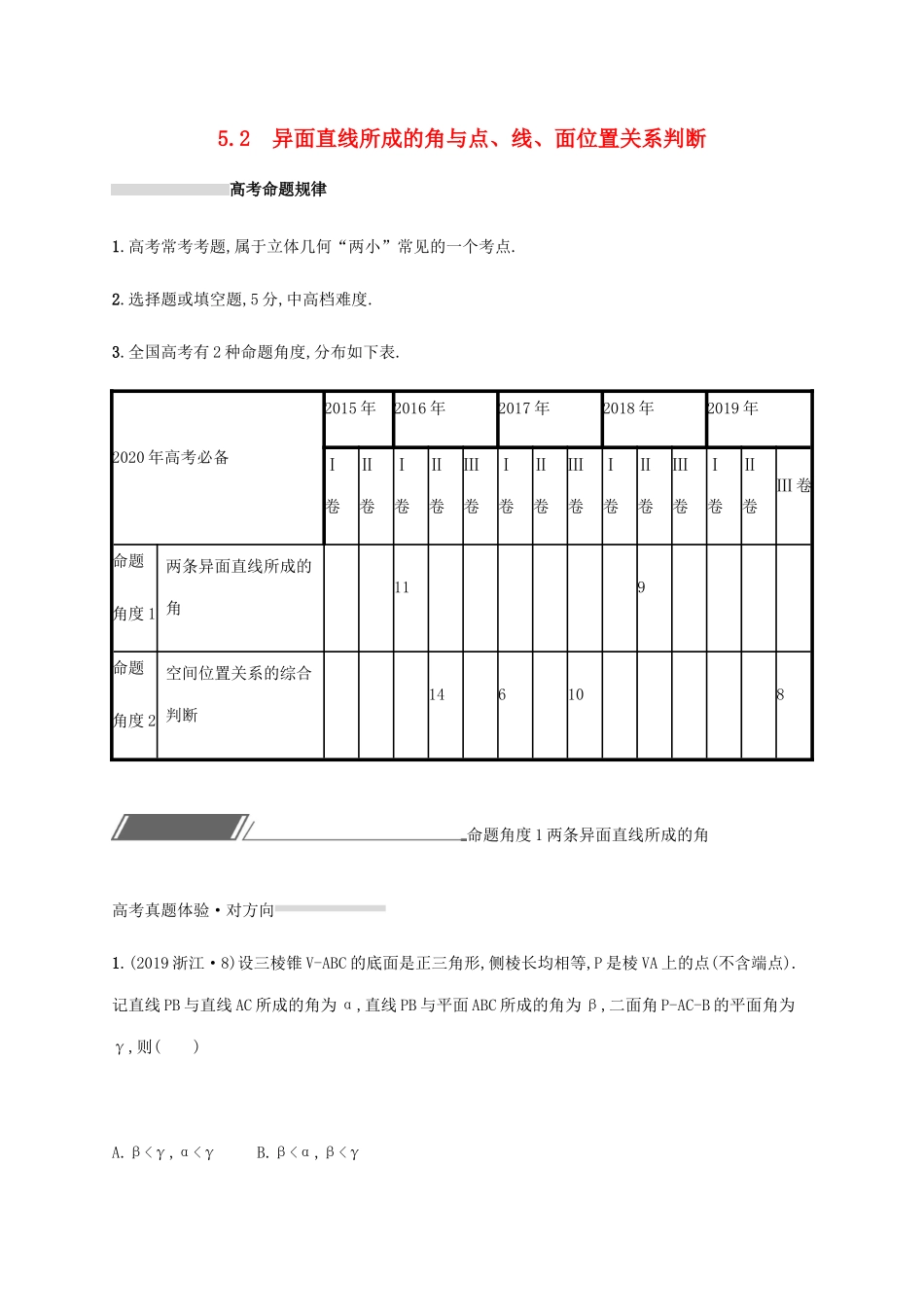
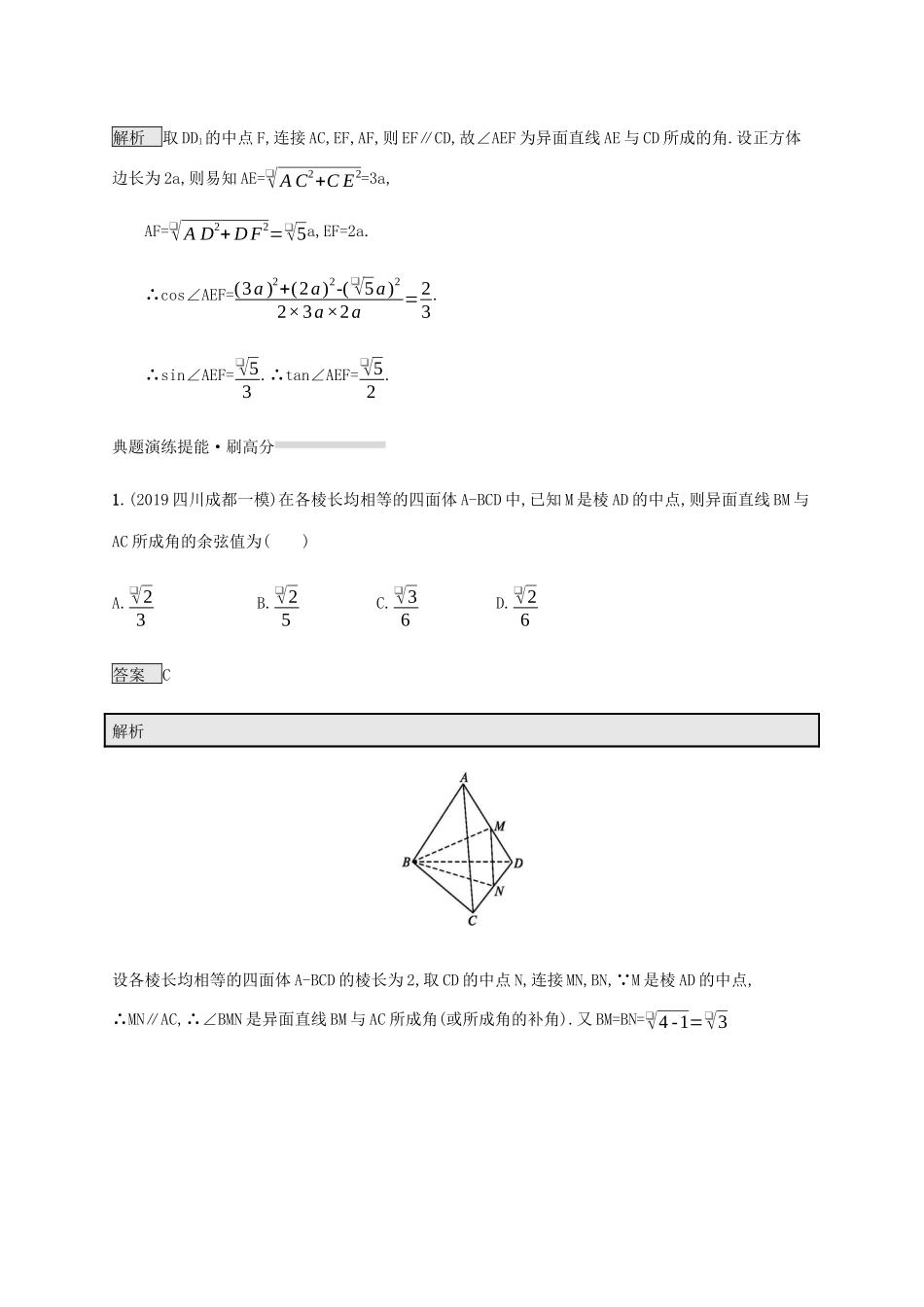
5.2异面直线所成的角与点、线、面位置关系判断高考命题规律1.高考常考考题,属于立体几何“两小”常见的一个考点.2.选择题或填空题,5分,中高档难度.3.全国高考有2种命题角度,分布如下表.2020年高考必备2015年2016年2017年2018年2019年Ⅰ卷Ⅱ卷Ⅰ卷Ⅱ卷Ⅲ卷Ⅰ卷Ⅱ卷Ⅲ卷Ⅰ卷Ⅱ卷Ⅲ卷Ⅰ卷Ⅱ卷Ⅲ卷命题角度1两条异面直线所成的角119命题角度2空间位置关系的综合判断146108命题角度1两条异面直线所成的角高考真题体验·对方向1.(2019浙江·8)设三棱锥V-ABC的底面是正三角形,侧棱长均相等,P是棱VA上的点(不含端点).记直线PB与直线AC所成的角为α,直线PB与平面ABC所成的角为β,二面角P-AC-B的平面角为γ,则()A.β<γ,α<γB.β<α,β<γC.β<α,γ<αD.α<β,γ<β答案B解析如图G为AC中点,点V在底面ABC上的投影为点O,则点P在底面ABC上的投影点D在线段AO上,过点D作DE垂直AE,易得PE∥VG,过点P作PF∥AC交VG于点F,过点D作DH∥AC,交BG于点H,则α=∠BPF,β=∠PBD,γ=∠PED,所以cosα=PFPB=EGPB=DHPBβ,因为tanγ=PDED>PDBD=tanβ,所以γ>β.故选B.2.(2018全国Ⅱ·9)在正方体ABCD-A1B1C1D1中,E为棱CC1的中点,则异面直线AE与CD所成角的正切值为()A.❑√22B.❑√32C.❑√52D.❑√72答案C解析取DD1的中点F,连接AC,EF,AF,则EF∥CD,故∠AEF为异面直线AE与CD所成的角.设正方体边长为2a,则易知AE=❑√AC2+CE2=3a,AF=❑√AD2+DF2=❑√5a,EF=2a.∴cos∠AEF=(3a)2+(2a)2-(❑√5a)22×3a×2a=23.∴sin∠AEF=❑√53.∴tan∠AEF=❑√52.典题演练提能·刷高分1.(2019四川成都一模)在各棱长均相等的四面体A-BCD中,已知M是棱AD的中点,则异面直线BM与AC所成角的余弦值为()A.❑√23B.❑√25C.❑√36D.❑√26答案C解析设各棱长均相等的四面体A-BCD的棱长为2,取CD的中点N,连接MN,BN, M是棱AD的中点,∴MN∥AC,∴∠BMN是异面直线BM与AC所成角(或所成角的补角).又BM=BN=❑√4-1=❑√3,MN=1,∴cos∠BMN=BM2+MN2-BN22×BM×MN=3+1-32×❑√3×1=❑√36,∴异面直线BM与AC所成角的余弦值为❑√36,故选C.2.在长方体ABCD-A1B1C1D1中,底面ABCD是边长为1的正方形,若其外接球的表面积为16π,则异面直线BD1与CC1所成的角的余弦值为.答案❑√144解析设外接球的半径为R,则4πR2=16π,解得R=2,设长方体的高为x,则x2+12+12=(2R)2=16,故x=❑√14,在Rt△BDD1中,∠DD1B即为异面直线所成的角,其余弦值为❑√144.3.(2019山东淄博一模)如图所示,平面BCC1B1⊥平面ABC,∠ABC=120°,四边形BCC1B1为正方形,且AB=BC=2,则异面直线BC1与AC所成角的余弦值为.答案❑√64解析由题意知,可将原图补为如图所示的直四棱柱. BC1∥AD,∴异面直线BC1与AC所成角即为直线AD与AC所成角∠DAC,由余弦定理可得AC2=AB2+BC2-2AB·BCcos∠ABC=4+4-8cos120°=12,∴AC=2❑√3.又AD=CD=❑√4+4=2❑√2,∴cos∠DAC=AD2+AC2-CD22AD·AC=8+12-82×2❑√2×2❑√3=❑√64.4.如图1,在矩形ABCD中,AB=2,BC=1,E是DC的中点;如图2,将△DAE沿AE折起,使折后平面DAE⊥平面ABCE,则异面直线AE和DB所成角的余弦值为.答案❑√66解析取AE的中点为O,连接DO,BO,延长EC到F使EC=CF,连接BF,DF,OF,则BF∥AE,所以∠DBF或它的补角为异面直线AE和DB所成角. DA=DE=1,∴DO⊥AE,且|AO|=|DO|=❑√22,在△ABO中,根据余弦定理得cos∠OAB=cos45°=|AO|2+|AB|2-|BO|22|AO|·|AB|=❑√22.∴|BO|=❑√102.同理可得|OF|=❑√262.又 平面DAE⊥平面ABCE,平面DAE∩平面ABCE=AE,DO⊂平面DAE,∴DO⊥平面ABCE. BO⊂平面ABCE,∴DO⊥BO,∴|BD|2=|BO|2+|DO|2=12+52=3,即|BD|=❑√3,同理可得|DF|=❑√7.又 BF=AE=❑√2,∴在△DBF中,cos∠DBF=|DB|2+|BF|2-|DF|22|DB|·|BF|=3+2-72×❑√3×❑√2=-❑√66, 两直线的夹角的取值范围为0,π2,∴异面直线AE和DB所成角的余弦值为❑√66.命题角度2空间位置关系的综合判断高考真题体验·对方向(2019全国Ⅲ·8)如图,点N为正方形ABCD的中心,△ECD为正三角形,平面ECD⊥平面ABCD,M是线段ED的中点,则()A.BM=EN,且直线BM,EN是相交直线B.BM≠EN,且直线BM,EN是相交直线C.BM=EN,且直线BM,EN是异面直线D.BM≠EN,且直线BM,EN是异面直线答案B解析如图,连接BD,BE.在△BDE...