正弦定理修改VIP免费

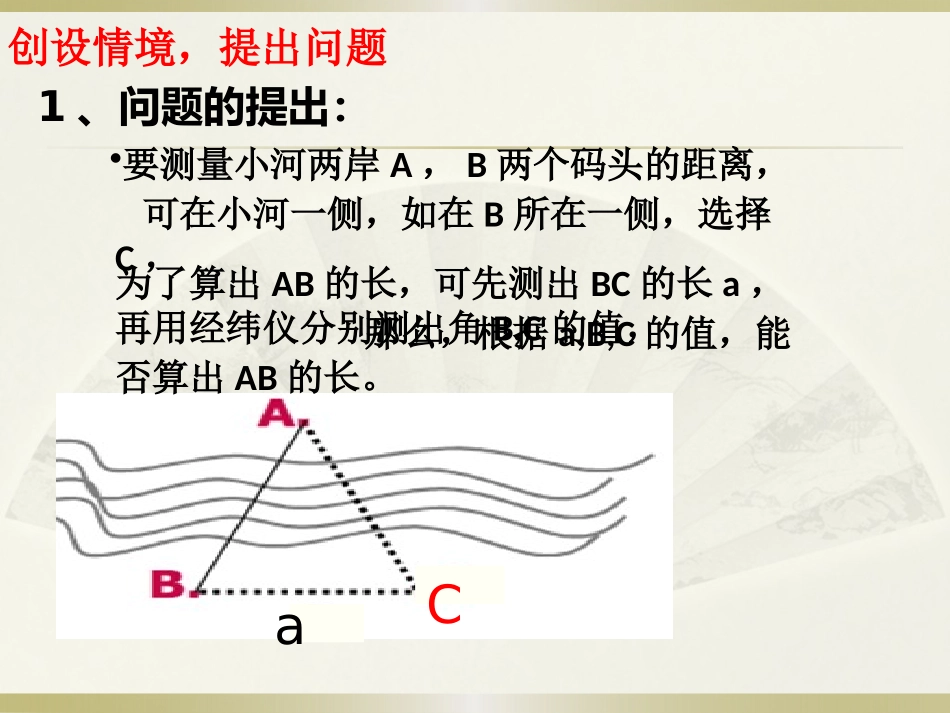
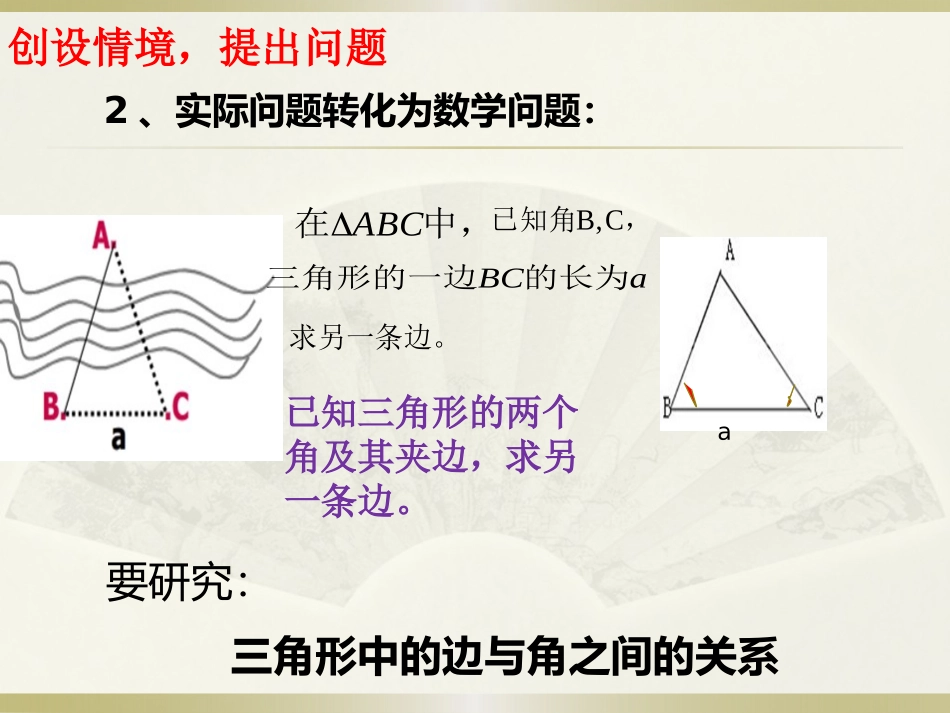
正弦定理班级：13级小教2班授课教师：丁丽创设情境，提出问题•要测量小河两岸A，B两个码头的距离，1、问题的提出：可在小河一侧，如在B所在一侧，选择C，Ca那么，根据a,B,C的值，能否算出AB的长。为了算出AB的长，可先测出BC的长a，再用经纬仪分别测出角B,C的值，创设情境，提出问题2、实际问题转化为数学问题：已知三角形的两个角及其夹边，求另一条边。中，在ABC求另一条边。，已知角CB,aBC的长为三角形的一边a要研究：三角形中的边与角之间的关系直角三角形中边角关系AsinBsinCsinAacsinBbcsinCccsinCcBbAasinsinsin在RtABC△中探寻特例，提出猜想ccacb90sincc1ccCsinCcBbAasinsinsin在锐角三角形中，逻辑推理，证明猜想作CD⊥AB于D，有AsinBsinBasinABCSc21c21同理，CabSABCsin21CabBcaAcbsin21sin21sin21各式同除以，abc21得到aAsin即CcBbAasinsinsinECDAB21cCsinbBsinbCDaCDAbsinBasinAbsinCD在锐角三角形中，有CcBbAasinsinsin在钝角三角行中，作AD⊥BC于D，中在ACDCsinADCbsinADBCSABC21Bacsin21cabsin21AbcSABCsin21CabBcaAcbsin21sin21sin21cCbBaAsinsinsinCcBbAasinsinsin逻辑推理，证明猜想cDAACDsinbADBcsin中ABDBsin)(180sinCbAD同理，bAD逻辑推理，证明猜想综上锐角三角形中钝角三角形中直角三角形中CcBbAasinsinsin正弦定理：CcBbAasinsinsin定理深化理解文字叙述：正弦定理：CcBbAasinsinsin方程的观点----对称美；和谐美在一个三角形中，结构特点：BbAasinsinCcBbsinsinCcAasinsin已知其中三个，求另一个。（1）已知两角和任一边，（2）已知两边和其中一边的对角，各边和它所对角正弦的比相等。引例：如图,1.48ma43B69C若测得求AB.解：)(180CBA)6943(180,68在△ABC中，由正弦定理得：ABAB68sin69sin1.48)(4.48m范例教学CsinAsinaACasinsin范例教学30,45,10CAcABCSB,,和ba例1：已知在△ABC中，求aa所以，)(180CAB解：因为又b所以，210CAcsinsin30sin45sin1075)3045(18042620256530sin105sin102175sin1075sin20AsinCsinc212210bBsincCsinCBcsinsin)13(2530,45,10CAcABCSB,,和ba例1：已知在△ABC中，求范例教学Abcsin21ABCS45sin10)265(212210)265(21210a75B2565b解：练习.120,30,12ABC1aBb求，Ａ＝中，、在A.C,,60,2,6ABC2求角中，、在Bcb小结：1、正弦定理CcBbAasinsinsin2、应用（1）已知两角3、三角形的面积公式。（2）已知两边和任一边，和其中一边的对角，解三角形.解三角形.ab21Csinac21Bsinbc21AsinABCS作业：练习册４１,63P