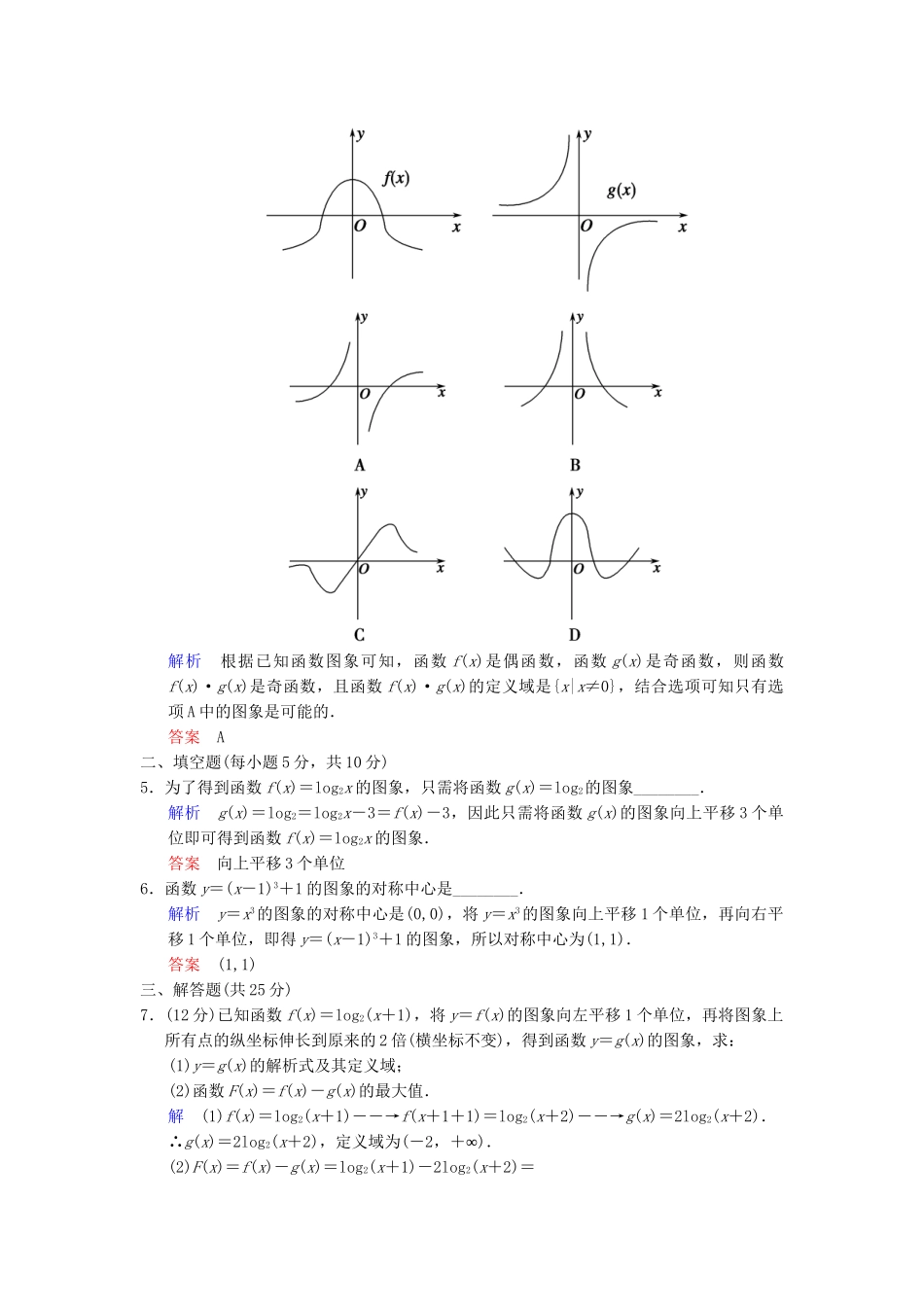
第7讲函数的图象分层A级基础达标演练(时间:30分钟满分:55分)一、选择题(每小题5分,共20分)1.(·大连模拟)函数y=5x与函数y=-的图象关于().A.x轴对称B.y轴对称C.原点对称D.直线y=x对称解析因为y=-=-5-x,所以关于原点对称.答案C2.(·兰州模拟)函数y=的图象大致是().解析由y=f(-x)==-f(x)知,函数为奇函数,排除A,B;当x=1时,y=0,排除C,故选D.答案D3.(·济南模拟)若loga2<0(a>0,且a≠1),则函数f(x)=loga(x+1)的图象大致是().解析 loga2<0,∴0
-1).令μ===,又因为(x+1)≥+2,当且仅当x=0时,等号成立,故μ≤.所以F(x)的最大值为-2.8.(13分)(·韶关调研)已知函数f(x)的图象与函数h(x)=x++2的图象关于点A(0,1)对称.(1)求f(x)的解析式;(2)若g(x)=f(x)+,且g(x)在区间(0,2]上为减函数,求实数a的取值范围.解(1)设f(x)图象上任一点P(x,y),则点P关于(0,1)点的对称点P′(-x,2-y)在h(x)的图象上,即2-y=-x-+2,∴y=f(x)=x+(x≠0).(2)g(x)=f(x)+=x+,g′(x)=1-. g(x)在(0,2]上为减函数,∴1≤-0在(0,2]上恒成立,即a+1≥x2在(0,2]上恒成立,∴a+1≥4,即a≥3,∴a的取值范围是[3∞,+).分层B级创新能力提升1.(·江西六校联考)函数f(x)=tanx+,x∈的大致图象为().解析当00,此时f(x)≥2,排除B,D;-0,得-0,f(x)>0;当x∈时,cosx>0,f(x)<0;当x∈时,cosx<0,f(x)<0.故不等式<0的解集为.答案4.(·唐山模拟)形如y=(a>0,b>0)“的函数,因其图象类似于汉字中的”字,故我们把“它称为”函数.若当a=1,b=1“时的”函数与函数y=lg|x|图象的交点个数为n,则n=________.解析由题易知,当a=1,b=1时,y==“在同一坐标系中画出”函数与函数y=lg|x|的图象如图所示,易知它们有4个交点.答案45.(·杭州二中月考)已知函数y=f(x)的定义域为R,并对一切实数x,都满足f(2+x)=f(2-x).(1)证明:函数y=f(x)的图象关于直线x=2对称;(2)若f(x)是偶函数,且x∈[0,2]时,f(x)=2x-1,求x∈[-4,0]时的f(x)的表达式.(1)证明设P(x0,y0)是函数y=f(x)图象上任一点,则y0=f(x0),点P关于直线x=2的对称点为P′(4-x0,y0).因为f(4-x0)=f[2+(2-x0)]=f[2-(2-x0)]=f(x0)=y0,所以P′也在y=f(x)的图象上,...