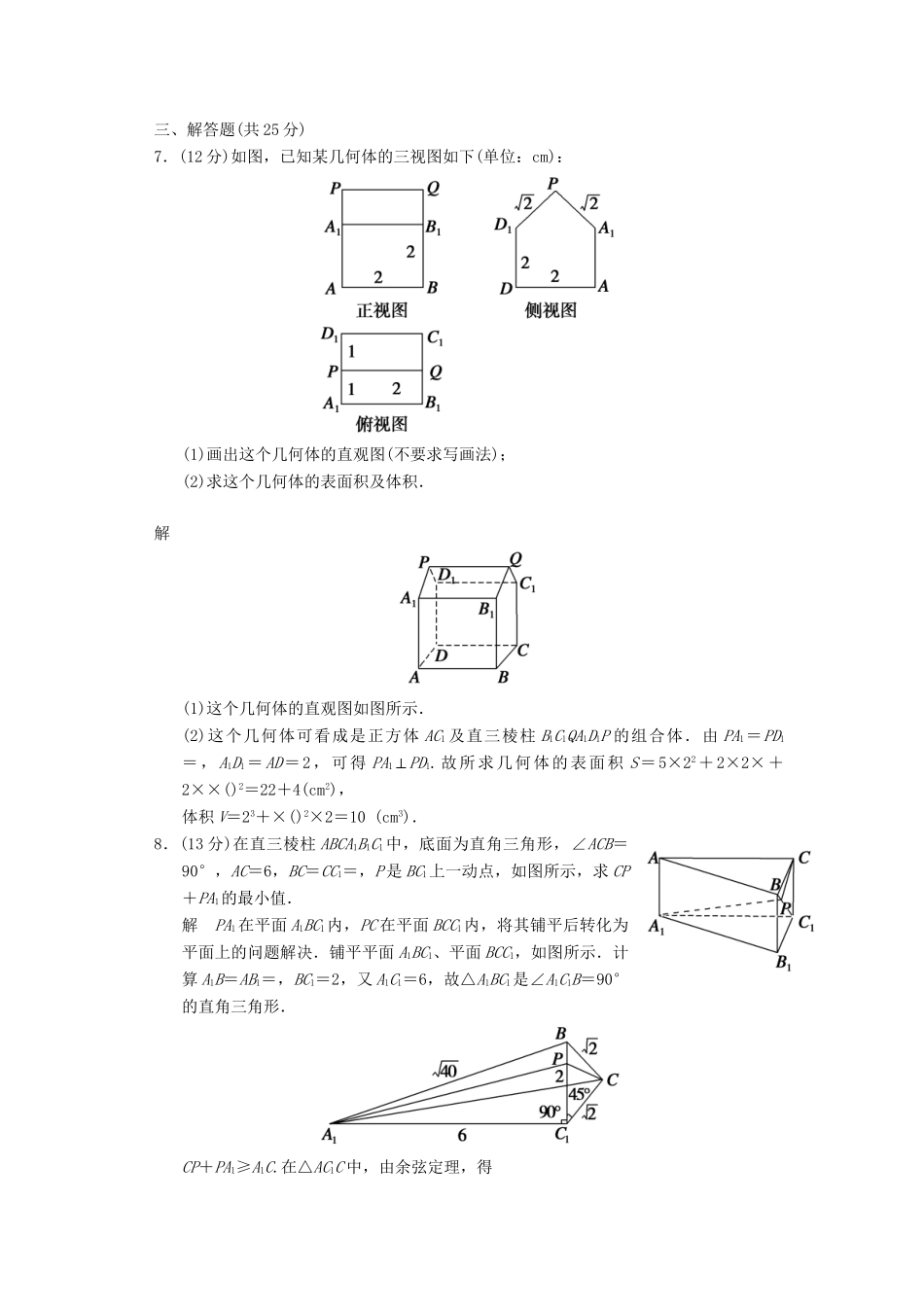
第2讲空间几何体的表面积与体积分层A级基础达标演练(时间:30分钟满分:55分)一、选择题(每小题5分,共20分)1.棱长为2的正四面体的表面积是().A.B.4C.4D.16解析每个面的面积为×2×2×=.∴正四面体的表面积为4.答案C2.(·江西卷)若一个几何体的三视图如图所示,则此几何体的体积为().A.B.5C.D.4解析由三视图可知该几何体为直六棱柱,且底面的面积为4,高为1,V=Sh=4,故选D.答案D3.(·新课标全国卷)平面α截球O的球面所得圆的半径为1,球心O到平面α的距离为,则此球的体积为().A.πB.4πC.4πD.6π解析如图,设截面圆的圆心为O′,M为截面圆上任一点,则OO′=,O′M=1,∴OM==,即球的半径为,∴V=π()3=4π.答案B4.一个几何体的三视图如图所示,那么此几何体的侧面积(单位:cm2)为().A.48B.64C.80D.120解析据三视图知,该几何体是一个正四棱锥(底面边长为8),直观图如图,PE为侧面△PAB的边AB上的高,且PE=5.∴此几何体的侧面积是S=4S△PAB=4××8×5=80.答案C二、填空题(每小题5分,共10分)5.已知S、A、B、C是球O表面上的点,SA⊥平面ABC,AB⊥BC,SA=AB=1,BC=,则球O的表面积等于________.解析将三棱锥SABC补形成以SA、AB、BC为棱的长方体,其对角线SC为球O的直径,所以2R=SC=2,R=1,∴表面积为4πR2=4π.答案4π6.(·湖北卷)已知某几何体的三视图如图所示,则该几何体的体积为________.解析由三视图知该几何体是由三个圆柱组成的,∴该几何体的体积为π×2×1×2+π×2×4=12π.答案12π三、解答题(共25分)7.(12分)如图,已知某几何体的三视图如下(单位:cm):(1)画出这个几何体的直观图(不要求写画法);(2)求这个几何体的表面积及体积.解(1)这个几何体的直观图如图所示.(2)这个几何体可看成是正方体AC1及直三棱柱B1C1QA1D1P的组合体.由PA1=PD1=,A1D1=AD=2,可得PA1⊥PD1.故所求几何体的表面积S=5×22+2×2×+2××()2=22+4(cm2),体积V=23+×()2×2=10(cm3).8.(13分)在直三棱柱ABCA1B1C1中,底面为直角三角形,∠ACB=90°,AC=6,BC=CC1=,P是BC1上一动点,如图所示,求CP+PA1的最小值.解PA1在平面A1BC1内,PC在平面BCC1内,将其铺平后转化为平面上的问题解决.铺平平面A1BC1、平面BCC1,如图所示.计算A1B=AB1=,BC1=2,又A1C1=6,故△A1BC1是∠A1C1B=90°的直角三角形.CP+PA1≥A1C.在△AC1C中,由余弦定理,得A1C===5,故(CP+PA1)min=5.分层B级创新能力提升1.(·哈尔滨模拟)某品牌香水瓶的三视图如下(单位:cm),则该几何体的表面积为().A.cm2B.cm2C.cm2D.cm2解析该几何体的上下为长方体,中间为圆柱.S表面积=S下长方体+S上长方体+S圆柱侧-2S圆柱底=2×4×4+4×4×2+2×3×3+4×3×1+2π××1-2×π2=94+.答案C2.(·福州模拟)如图所示,已知三棱柱ABCA1B1C1的所有棱长均为1,且AA1⊥底面ABC,则三棱锥B1ABC1的体积为().A.B.C.D.解析三棱锥B1ABC1的体积等于三棱锥AB1BC1的体积,三棱锥AB1BC1的高为,底面积为,故其体积为××=.答案A3.(·江西盟校二联)已知某几何体的直观图及三视图如图所示,三视图的轮廓均为正方形,则该几何体的表面积为________.解析借助常见的正方体模型解决.由三视图知,该几何体由正方体沿面AB1D1与面CB1D1截去两个角所得,其表面由两个等边三角形、四个直角三角形和一个正方形组成.计算得其表面积为12+4.答案12+44.(·长春二模)如图所示,正方体ABCDA1B1C1D1的棱长为6,则以正方体ABCDA1B1C1D1的中心为顶点,以平面AB1D1截正方体外接球所得的圆为底面的圆锥的全面积为________.解析设O为正方体外接球的球心,则O也是正方体的中心,O到平面AB1D1的距离是体对角线长的,即为.又球的半径是正方体对角线长的一半,即为3,由勾股定理可知,截面圆的半径为=2,圆锥底面面积为S1=π·(2)2=24π,圆锥的母线即为球的半径3,圆锥的侧面积为S2=π×2×3=18π.因此圆锥的全面积为S=S2+S1=18π+24π=(18+24)π.答案(18+24)π5.(·杭州模拟)如图,在四边形ABCD中,∠DAB=90°,∠ADC=135°,AB=5,CD=2,AD=2,求四边形ABCD...