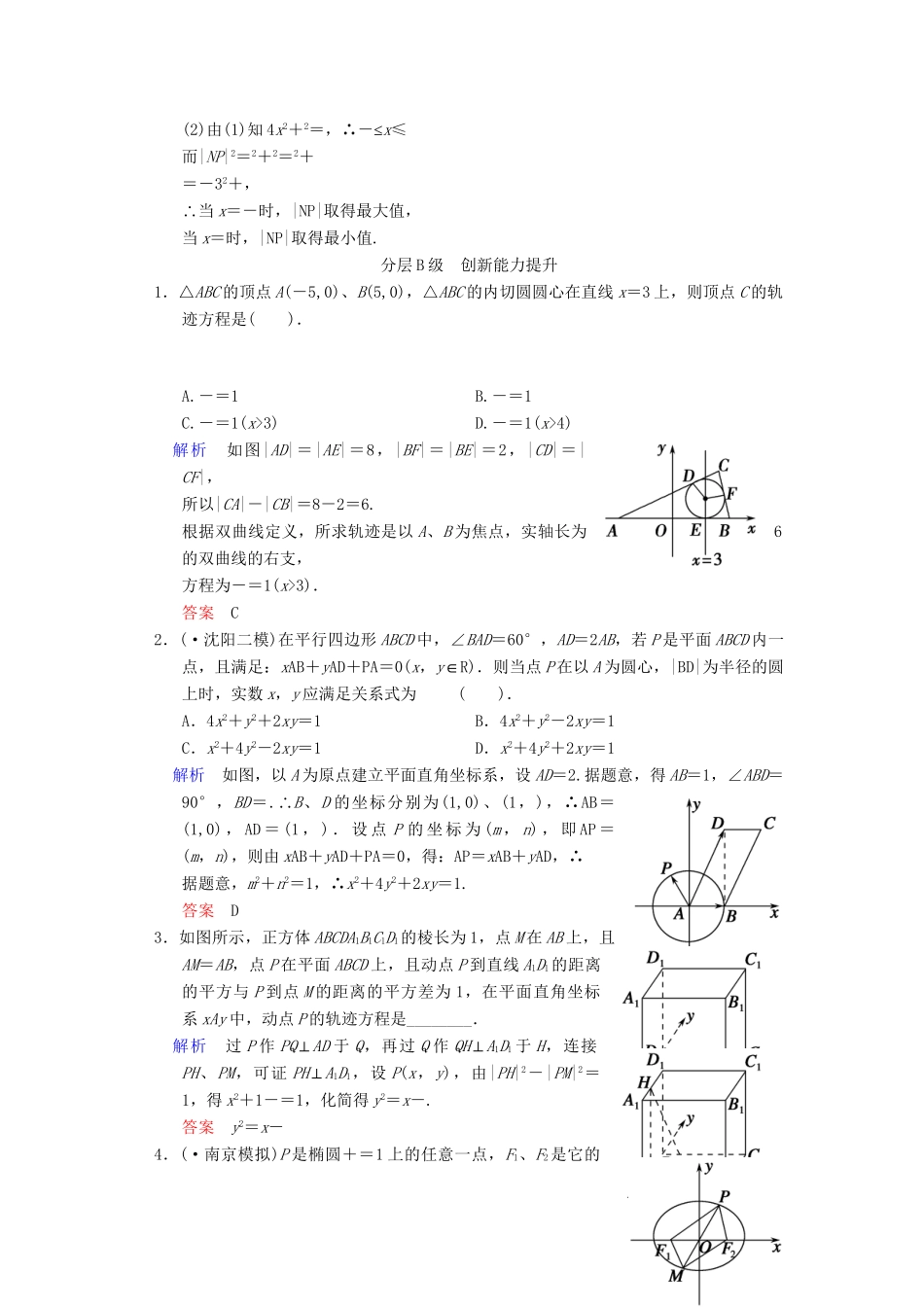
第8讲曲线与方程分层A级基础达标演练(时间:30分钟满分:55分)一、选择题(每小题5分,共20分)1.动点P(x,y)满足5=|3x+4y-11|,则点P的轨迹是().A.椭圆B.双曲线C.抛物线D.直线解析设定点F(1,2),定直线l:3x+4y-11=0,则|PF|=,点P到直线l的距离d=.由已知得=1,但注意到点F(1,2)恰在直线l上,所以点P的轨迹是直线.选D.答案D2.(·榆林模拟)若点P到直线x=-1的距离比它到点(2,0)的距离小1,则点P的轨迹为().A.圆B.椭圆C.双曲线D.抛物线解析依题意,点P到直线x=-2的距离等于它到点(2,0)的距离,故点P的轨迹是抛物线.答案D3.(·临川模拟)设圆(x+1)2+y2=25的圆心为C,A(1,0)是圆内一定点,Q为圆周上任一点.线段AQ的垂直平分线与CQ的连线交于点M,则M的轨迹方程为().A.-=1B.+=1C.-=1D.+=1解析M为AQ垂直平分线上一点,则|AM|=|MQ|,∴|MC|+|MA|=|MC|+|MQ|=|CQ|=5,故M的轨迹为椭圆,∴a=,c=1,则b2=a2-c2=,∴椭圆的标准方程为+=1.答案D4.(·烟台月考)已知点P是直线2x-y+3=0上的一个动点,定点M(-1,2),Q是线段PM延长线上的一点,且|PM|=|MQ|,则Q点的轨迹方程是().A.2x+y+1=0B.2x-y-5=0C.2x-y-1=0D.2x-y+5=0解析由题意知,M为PQ中点,设Q(x,y),则P为(-2-x,4-y),代入2x-y+3=0,得2x-y+5=0.答案D二、填空题(每小题5分,共10分)5.(·泰州月考)在△ABC中,A为动点,B、C为定点,B,C(a>0),且满足条件sinC-sinB=sinA,则动点A的轨迹方程是________.解析由正弦定理,得-=×,∴|AB|-|AC|=|BC|,且为双曲线右支.答案-=1(x>0且y≠0)6.如图,点F(a,0)(a>0),点P在y轴上运动,M在x轴上运动,N为动点,且PM·PF=0,PM+PN=0,则点N的轨迹方程为________.解析由题意,知PM⊥PF且P为线段MN的中点,连接FN,延长FP至点Q使P恰为QF之中点;连接QM,QN,则四边形FNQM为菱形,且点Q恒在直线l:x=-a上,故点N的轨迹是以点F为焦点,直线l为准线的抛物线,其方程为:y2=4ax.答案y2=4ax三、解答题(共25分)7.(12分)已知长为1+的线段AB的两个端点A、B分别在x轴、y轴上滑动,P是AB上一点,且AP=PB,求点P的轨迹C的方程.解设A(x0,0),B(0,y0),P(x,y),AP=PB,又AP=(x-x0,y),PB=(-x,y0-y),所以x-x0=-x,y=(y0-y),得x0=x,y0=(1+)y.因为|AB|=1+,即x+y=(1+)2,所以2+[(1+)y]2=(1+)2,化简得+y2=1.∴点P的轨迹方程为+y2=1.8.(13分)设椭圆方程为x2+=1,过点M(0,1)的直线l交椭圆于A,B两点,O为坐标原点,点P满足OP=(OA+OB),点N的坐标为,当直线l绕点M旋转时,求:(1)动点P的轨迹方程;(2)|NP|的最大值,最小值.解(1)直线l过定点M(0,1),当其斜率存在时设为k,则l的方程为y=kx+1.设A(x1,y1),B(x2,y2),由题意知,A、B的坐标满足方程组消去y得(4+k2)x2+2kx-3=0.则Δ=4k2+12(4+k2)>0.∴x1+x2=-,x1x2=.P(x,y)是AB的中点,则由消去k得4x2+y2-y=0.当斜率k不存在时,AB的中点是坐标原点,也满足这个方程,故P点的轨迹方程为4x2+y2-y=0.(2)由(1)知4x2+2=,∴≤-x≤而|NP|2=2+2=2+=-32+,∴当x=-时,|NP|取得最大值,当x=时,|NP|取得最小值.分层B级创新能力提升1.△ABC的顶点A(-5,0)、B(5,0),△ABC的内切圆圆心在直线x=3上,则顶点C的轨迹方程是().A.-=1B.-=1C.-=1(x>3)D.-=1(x>4)解析如图|AD|=|AE|=8,|BF|=|BE|=2,|CD|=|CF|,所以|CA|-|CB|=8-2=6.根据双曲线定义,所求轨迹是以A、B为焦点,实轴长为6的双曲线的右支,方程为-=1(x>3).答案C2.(·沈阳二模)在平行四边形ABCD中,∠BAD=60°,AD=2AB,若P是平面ABCD内一点,且满足:xAB+yAD+PA=0(x,y∈R).则当点P在以A为圆心,|BD|为半径的圆上时,实数x,y应满足关系式为().A.4x2+y2+2xy=1B.4x2+y2-2xy=1C.x2+4y2-2xy=1D.x2+4y2+2xy=1解析如图,以A为原点建立平面直角坐标系,设AD=2.据题意,得AB=1,∠ABD=90°,BD=.∴B、D的坐标分别为(1,0)、(1,),∴AB=(1,0),AD=(1,).设点P的坐标为(m,n),即AP=(m,n),...