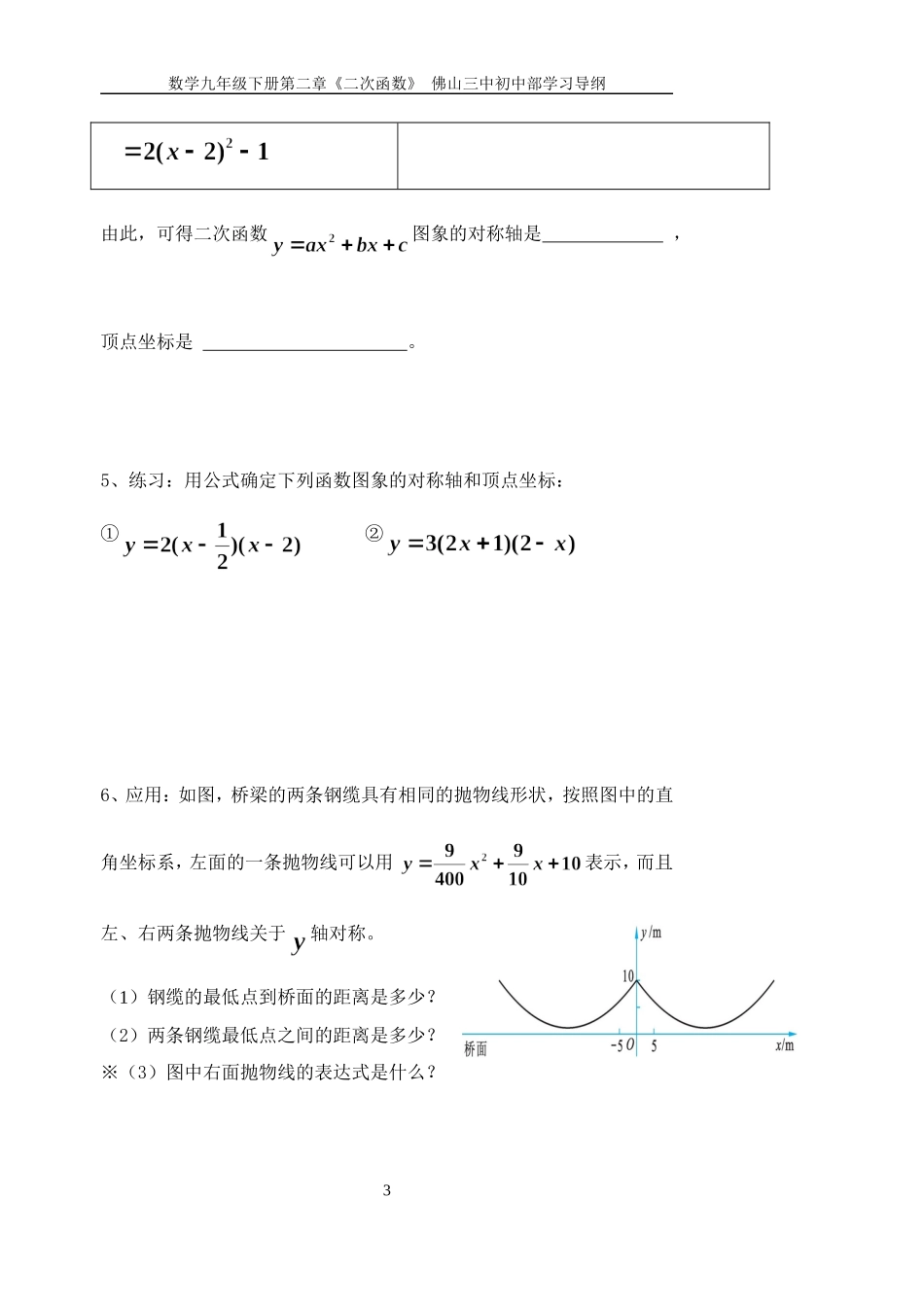
⑤④数学九年级下册第二章《二次函数》佛山三中初中部学习导纲课题:二次函数的图象与性质(4)时间:2014-12班别学号:学生姓名:一、【学习目标】能用配方法将形如的关系式化成的形式,能运用公式法确定函数的对称轴和顶点坐标。二、【重点】能用配方法将形如的关系式化成的形式,能运用公式确定函数的对称轴和顶点坐标。【难点】能用配方法将形如的关系式化成的形式,能运用公式确定函数的对称轴和顶点坐标。三、【知识回顾】的图象可看成是的图象先向平移个单位长度,再向平移个单位长度所得。它的开口方向是,对称轴是,顶点坐标是。当=时,的值最,且为。当时,的值随值的增大而增大;当时,的值随值的增大而减小。四、【学习新知】1、例1求二次函数图象的对称轴和顶点坐标。(提示:可否能将化成的形式)1数学九年级下册第二章《二次函数》佛山三中初中部学习导纲2、练习:用配方法确定下列函数图象的对称轴和顶点坐标:①②③④3、思考:在对上题中的③、④进行配方时遇到什么困难?可以用什么方法解决此困难?(提示:联想在解一元二次方程时,遇到若使用配方法运算时比较困难,我们可以选择公式求解)4、例2求二次函数图象的对称轴和顶点坐标。(提示:参考用配方法将化为的形式的步骤,将化为的形式)2数学九年级下册第二章《二次函数》佛山三中初中部学习导纲由此,可得二次函数图象的对称轴是,顶点坐标是。5、练习:用公式确定下列函数图象的对称轴和顶点坐标:①②6、应用:如图,桥梁的两条钢缆具有相同的抛物线形状,按照图中的直角坐标系,左面的一条抛物线可以用表示,而且左、右两条抛物线关于轴对称。(1)钢缆的最低点到桥面的距离是多少?(2)两条钢缆最低点之间的距离是多少?※(3)图中右面抛物线的表达式是什么?3数学九年级下册第二章《二次函数》佛山三中初中部学习导纲五、【课堂小结】可以使用什么样的方法将形如的关系式化成的形式,然后确定函数的对称轴和顶点坐标。六、【课后巩固】1、用适当的方法确定下列函数图象的对称轴和顶点坐标:(1)(2)(3)(4)2、将二次函数的图象向上平移2个单位长度,再向左平移3个单位长度,得到抛物线,求、的值,并求出4数学九年级下册第二章《二次函数》佛山三中初中部学习导纲这条抛物线的开口方向、对称轴和顶点坐标,必要时画草图进行验证。3、当火箭被竖直向上发射时,它的高度h(m)与时间t(s)的关系可以用公式表示。经过多长时间,火箭到达它的最高点?最高点的高度是多少?5