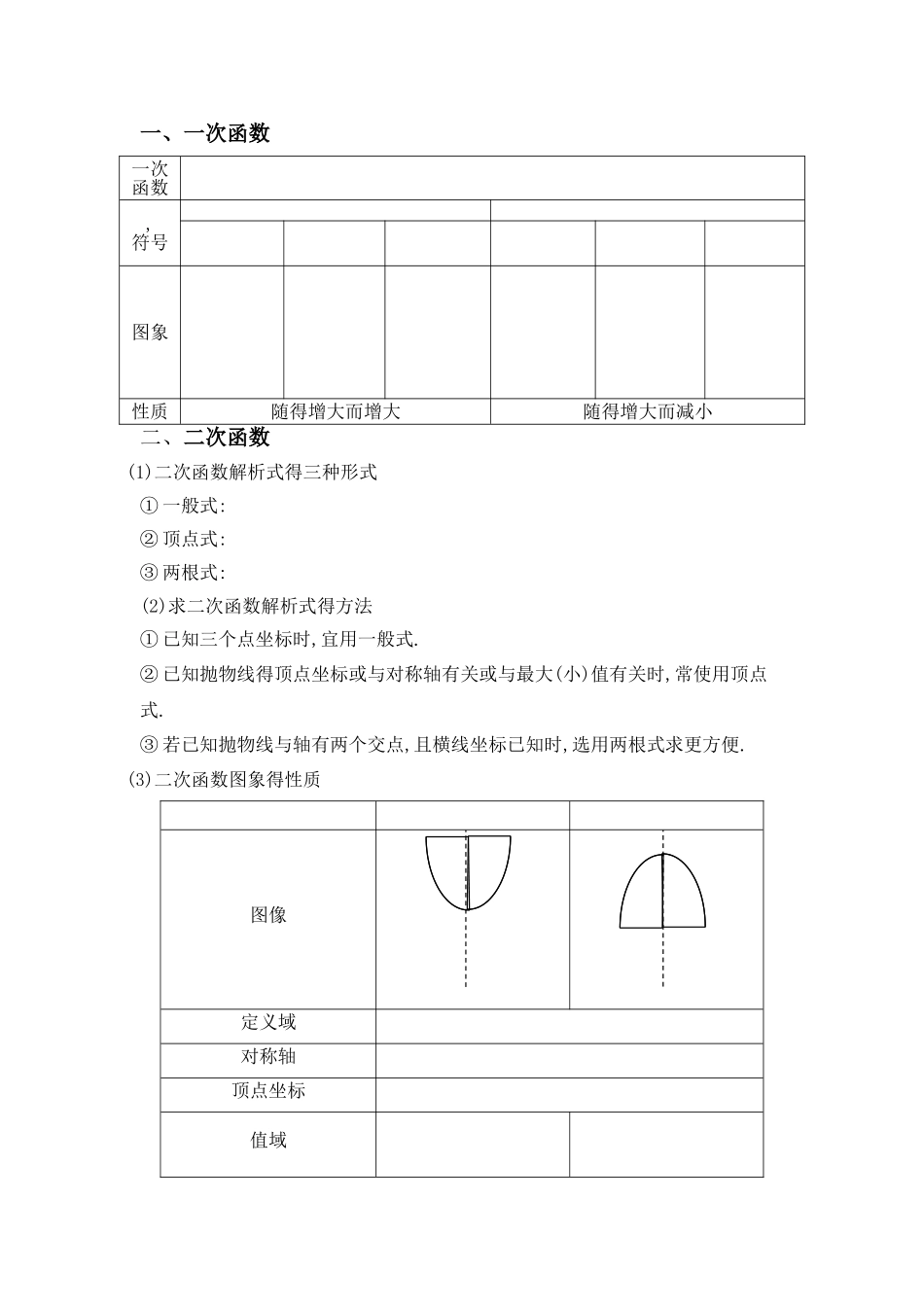
一、一次函数一次函数,符号图象性质随得增大而增大随得增大而减小二、二次函数(1)二次函数解析式得三种形式① 一般式:② 顶点式:③ 两根式:(2)求二次函数解析式得方法① 已知三个点坐标时,宜用一般式.② 已知抛物线得顶点坐标或与对称轴有关或与最大(小)值有关时,常使用顶点式.③ 若已知抛物线与轴有两个交点,且横线坐标已知时,选用两根式求更方便.(3)二次函数图象得性质图像定义域对称轴顶点坐标值域单调区间递减递增递增递减①、二次函数得图象就是一条抛物线,对称轴方程为顶点坐标就是② 当时,抛物线开口向上,函数在上递减,在上递增,当时,;当时,抛物线开口向下,函数在上递增,在上递减,当时,.三、幂函数(1)幂函数得定义 一般地,函数叫做幂函数,其中为自变量,就是常数.(2)幂函数得图象过定点:所有得幂函数在都有定义,并且图象都通过点. 四、指数函数(1)根式得概念假如,且,那么叫做得次方根.(2)分数指数幂得概念① 正数得正分数指数幂得意义就是:且.0 得正分数指数幂等于 0.② 正数得负分数指数幂得意义就是:且.0 得负分数指数幂没有意义. (3)运算性质① ②③(4)指数函数函数名称指数函数定义函数且叫做指数函数图象定义域值域过定点图象过定点,即当时,.奇偶性非奇非偶单调性在上就是增函数在上就是减函数函数值得变化情况变化对图象得影响在第一象限内,越大图象越高;在第二象限内,越大图象越低.五、对数函数(1)对数得定义0101① 若,则叫做以为底得对数,记作,其中叫做底数,叫做真数.② 负数与零没有对数.③ 对数式与指数式得互化:.(2)几个重要得对数恒等式,,.(3)常用对数与自然对数常用对数:,即;自然对数:,即(其中…).(4)对数得运算性质 假如,那么① 加法: ② 减法:③ 数乘: ④⑤ ⑥ 换底公式:(5)对数函数函数名称对数函数定义函数且叫做对数函数图象定义域值域过定点图象过定点,即当时,.奇偶性非奇非偶单调性在上就是增函数在上就是减函数函数值得变化情况变化对 图象得影响在第一象限内,越大图象越靠低;在第四象限内,越大图象越靠高.(6)反函数得概念设函数得定义域为,值域为,从式子中解出,得式子.假如对于在中得任何一个值,通过式子,在中都有唯一确定得值与它对应,那么式子表示就是得函数,函数叫做函数得反函数,记作,习惯上改写成.(7)反函数得求法① 确定反函数得定义域,即原函数得值域;② 从原函数式中反解出;③ 将改写成,并注明反函数得定义域.(8)反函数得性质 ① 原函数与反函数得图象关于直线对称.② 函数...