线性规划复习课VIP免费

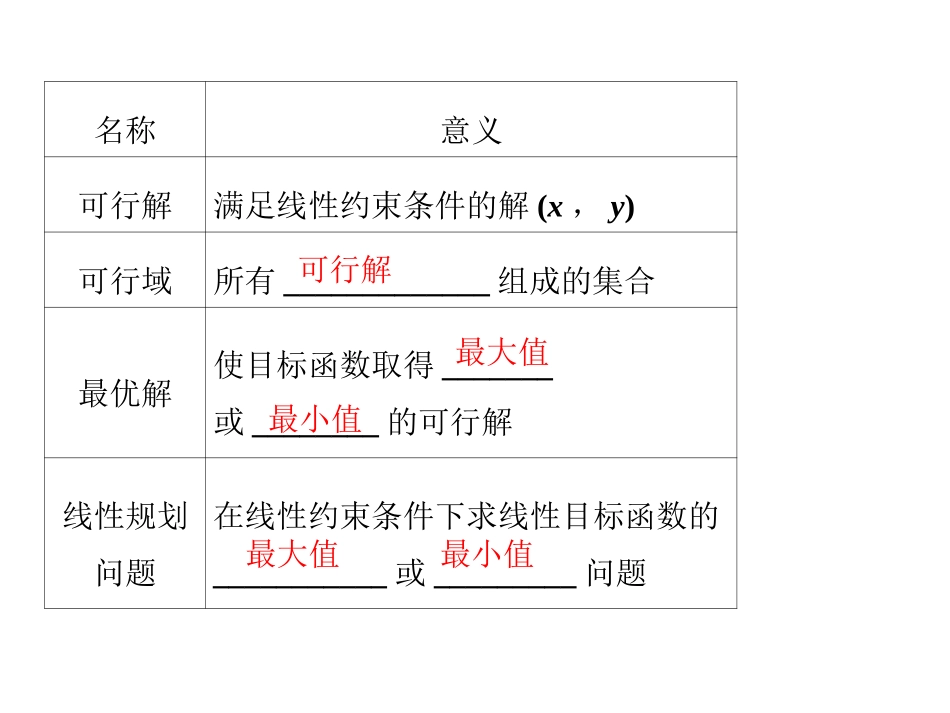
二元一次不等式(组)与简单线性规划（复习课）名称意义约束条件由变量x，y组成的_______________线性约束条件由x，y的_________不等式(或方程)组成的不等式组目标函数关于x，y的函数_____________线性目标函数关于x，y的________解析式不等式(组)一次解析式一次函数130,0xyxyxyaxbyzbyaxzbyaxz22知识梳理名称意义可行解满足线性约束条件的解(x，y)可行域所有_____________组成的集合最优解使目标函数取得_______或________的可行解线性规划问题在线性约束条件下求线性目标函数的___________或_________问题可行解最大值最小值最大值最小值确定平面区域的方法：（1）直线定界（2）定域①特殊点定域②当A>0时，表示直线右侧的区域；表示直线左侧的区域。0CByAx0CByAx0CByAx0CByAx课内探究案例：已知变量x，y满足约束条件，完成以下探究和变式：144222yxyxyx探究一：求目标函数yxz2的最值1minz4maxz22yx42yx1--4yxxy方法一：1.作出可行域2.将线性目标函数化为斜截式，分析目标函数的几何意义（在y轴上的截距或其相反数）3.令z=0，作直线0=ax+by,平移直线，确定最优解4.将点的坐标代入目标函数。方法二：目标函数的最优解一般在区域的顶点或边界处取得，可解出可行域的顶点，后将坐标代入目标函数求出，再检验。:0l0l归纳小结：求线性目标函数最值的方法：0ayaxza变式一在本例条件下，若目标函数取得最大值的最优解不唯一，则的值为。222yx42yx1--4yxxy14yx探究二：求的取值范围221-yxz437,5122yx42yx1--4yxxy14yx变式二：（1）求的取值范围1222yxxz445,222yx42yxxy14yx探究三：目标函数的取值范围是11xyz38,31xy22yx42yx14yx变式三：（1）目标函数的取值范围是，，12--1-1xyzxy22yx42yx14yx（2）目标函数的取值范围是132xyxz319,3511211221132xyxyxxyxz思考：在不等式组确定的平面区中，若的最大值为3，则的值是（）ayyxyx00yxz2aA．1B．2C．3D．4巩固练习已知变量x,y满足（1）求的最大值（2）求的最小值102553034xyxyxyxz34xyz总结提升反思总结1．利用平面区域求目标函数的最值步骤(1)作出可行域；(2)找到目标函数对应的最优解对应点；(3)代入目标函数求最值．2．常见的目标函数(1)形如z＝ax＋by的截距型；(2)形如z＝y－ax－b的斜率型；(3)形如z＝(x－a)2＋(y－b)2的距离型．3．线性目标函数的最值点，一般在可行域的顶点或边界上取得．