双曲线的几何性质 (2)VIP免费

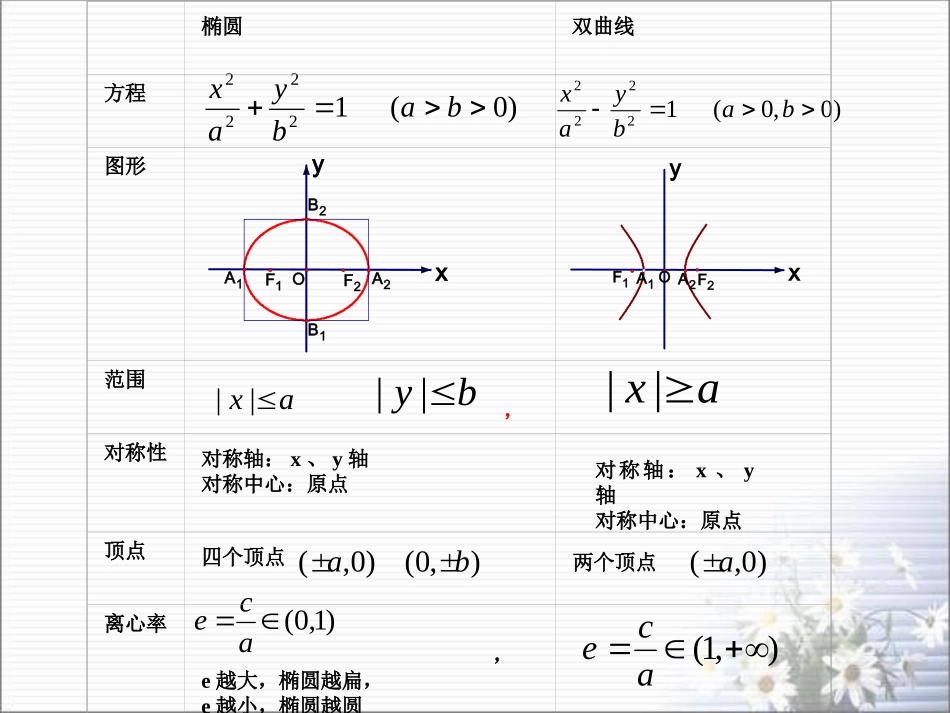
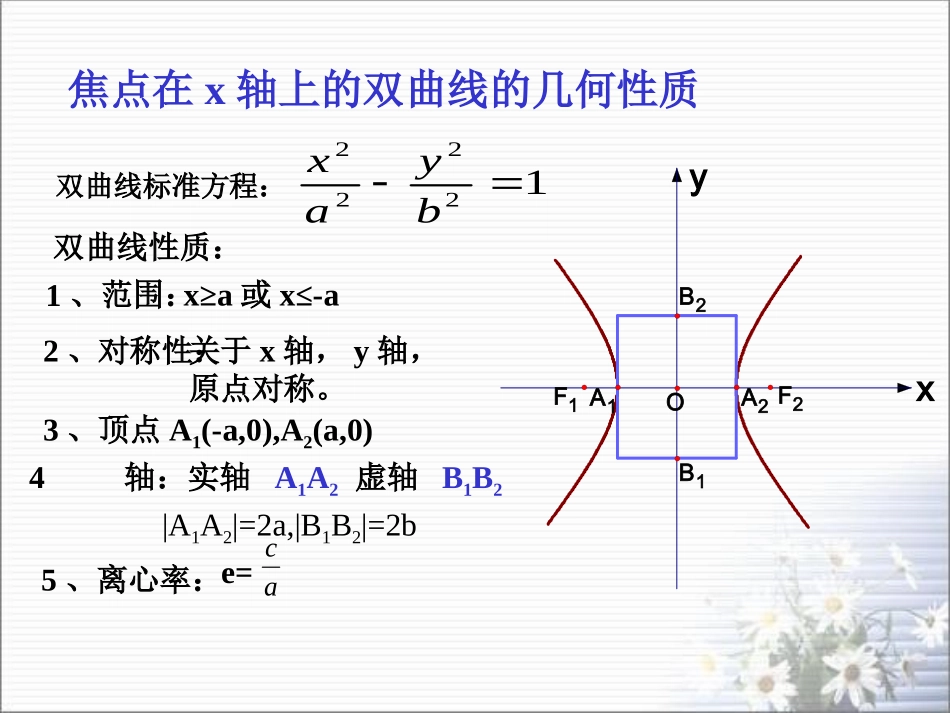
双曲线的定义及标准方程双曲线的几何性质)0(12222babyax)0,0(12222babyaxyxF1F2OA2B2A1B1yxA1F1F2OA2ax||by||)0,(a),0(b)1,0(ace椭圆双曲线方程图形范围，对称性对称轴：x、y轴对称中心：原点顶点四个顶点离心率，e越大，椭圆越扁，e越小，椭圆越圆ax||对称轴：x、y轴对称中心：原点两个顶点)0,(a),1(ace焦点在x轴上的双曲线的几何性质双曲线标准方程：12222byax双曲线性质：1、范围：x≥a或x≤-a2、对称性：关于x轴，y轴，原点对称。3、顶点A1(-a,0),A2(a,0)4轴：实轴A1A2虚轴B1B25、离心率：e=acxyB1B2OF2F1A2A1|A1A2|=2a,|B1B2|=2b根据以上几何性质能够较准确地画出椭圆的图形？yxF1F2OA2B2A1B1根据以上几何性质能否较准确地画出双曲线的图形呢？C1xyOC2C3YXF1F2A1A2B1B212222byax焦点在x轴上的双曲线图像xaby渐进线方程：离心率对双曲线形状的影响开口越大离心率越大，双曲线的XYF1F2OB1B2A2A112222bxay焦点在y轴上的双曲线图像焦点在y轴上的双曲线的几何性质双曲线标准方程：YX12222bxayxbay双曲线性质：1、范围：y≥a或y≤-a2、对称性：关于x轴，y轴，原点对称。3、顶点A1（0，-a），A2（0，a）4、轴：实轴A1A2;虚轴B1B2B1B2A1A25、渐近线方程：6、离心率：e=c/aF2F2o例:求双曲线14416922yx的实半轴长,虚半轴长,焦点坐标,离心率.渐近线方程。解：把方程化为标准方程：1342222xy可得:实半轴长a=453422虚半轴长b=3半焦距c=焦点坐标是(0,-5),(0,5)离心率:45ace渐近线方程:xy34例：双曲线116222byx的实轴的一个端点A1，虚轴的一个端点为B1，且|A1B1|=5，求双曲线的标准方程。OA1xyB1例.双曲线14922yx19422xy的渐近线方程是OF2F1A1A2xyB1B2F2F1xy32已知双曲线的虚轴为实轴,实轴为虚轴的双曲线叫原双曲线的共轭双曲线渐近线方程是xy32的双曲线标准方程且过点共渐近线例：求与双曲线3,32,191622Ayx的双曲线标准方程，且过点为例：求两条渐近线方程13,3Pxy例.已知实轴和虚轴等长的双曲线叫做等轴双曲线，求等轴双曲线的渐近线以及离心率。等轴双曲线方程：222ayx或222axy渐进线方程：0yx离心率：2e)0(12222babyax)0,0(12222babyaxyxF1F2OA2B2A1B1yxA1F1F2OA2ax||ay||)0,(a),0(b)1,0(ace椭圆双曲线方程图形范围，对称性对称轴：x、y轴对称中心：原点顶点四个顶点离心率，e越大，椭圆越扁，e越小，椭圆越圆ax||对称轴：x、y轴对称中心：原点两个顶点)0,(a),1(ace掌握双曲线的简单的几何性质双曲线的几何性质的简单应用思考题:以已知双曲线的虚轴为实轴,实轴为虚轴的双曲线叫原双曲线的共轭双曲线,求证:(1)双曲线和它的共轭双曲线有共同的渐近线;(2)双曲线和它的共轭双曲线的四个焦点在同一个圆上.YXA1A2B1B2F1F2oF’2F’1证明:(1)设已知双曲线的方程是:12222byax则它的共轭双曲线方程是:12222axby渐近线为：0byax渐近线为:0axby可化为：0byax故双曲线和它的共轭双曲线有共同的渐近线(2)设已知双曲线的焦点为F(c,0),F(-c,0)它的共轭双曲线的焦点为F1(0,c),F2(0,-c),∵22bac22bac∴c=c'所以四个焦点F1,F2,F3,F4在同一个圆.2222上bayx问:有相同渐近线的双曲线方程一定是共轭双曲线吗？的双曲线标准方程虚轴长为为例：求两条渐进线方程6,32xyeMFFFFM则离心率且，两个焦点为点为例：双曲线虚轴一个端120,2121