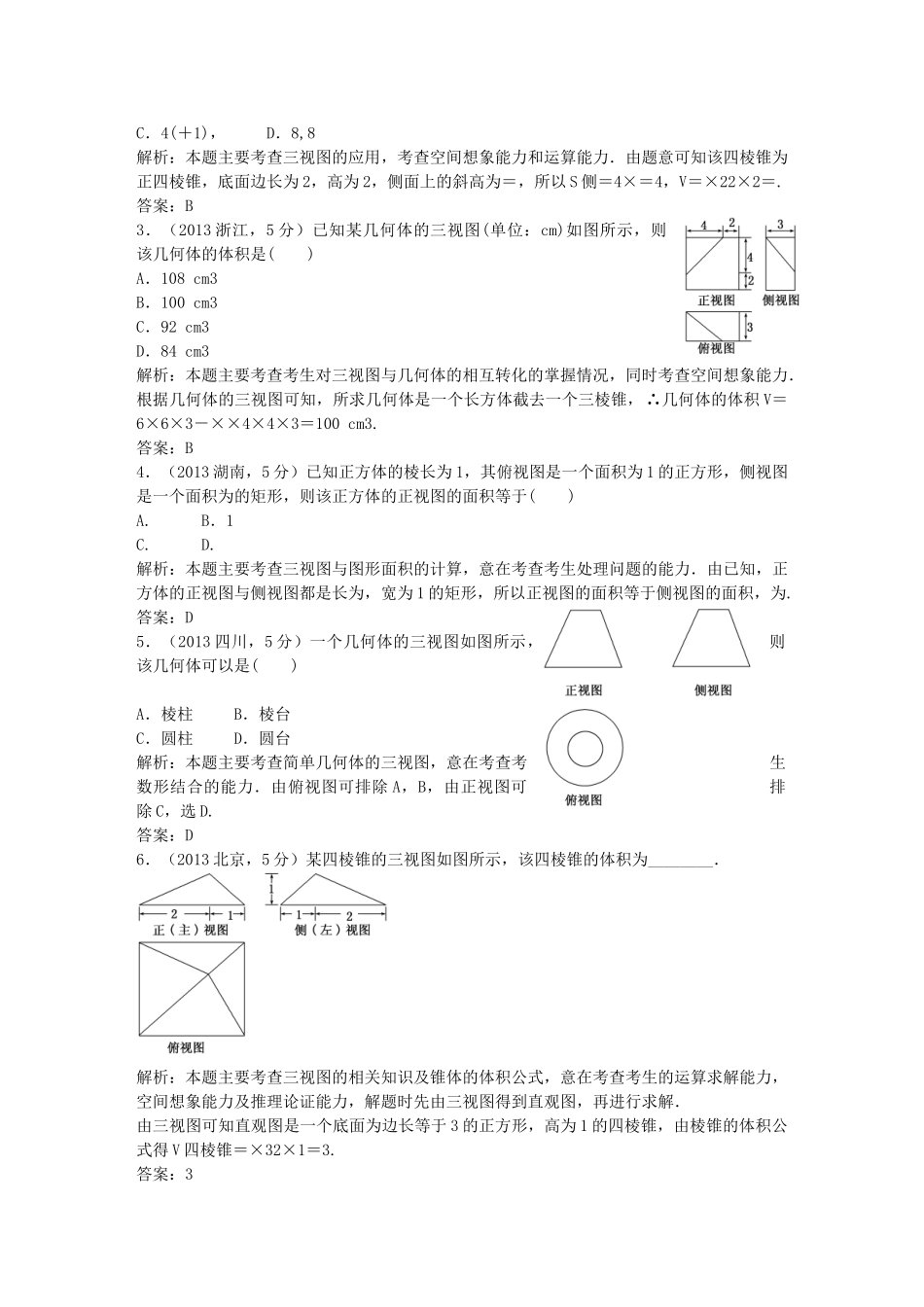
2009~2013年高考真题备选题库第7章立体几何第1节空间几何体的结构特征及三视图与直观图考点一柱、锥、台、球及其简单几何体的结构特征1.(2013北京,5分)如图,在正方体ABCDA1B1C1D1中,P为对角线BD1的三等分点,则P到各顶点的距离的不同取值有()A.3个B.4个C.5个D.6个解析:本题主要考查空间几何体及三角形中的边角关系,意在考查考生的空间想象能力和空间构造能力.解决本题的关键是构造直角三角形.在Rt△D1DB中,点P到点D1,D,B的距离均不相等,在Rt△D1CB中,点P到点C的距离与点P到点D1,D,B的距离均不相等,在Rt△D1A1B中,点P到点A1的距离与点P到点D的距离相等,在Rt△D1C1B中,点P到点C1的距离与点P到点D的距离相等,在Rt△D1B1B中,点P到点A的距离与点P到点C的距离相等,在Rt△D1AB中,点P到点A的距离与点P到点C的距离相等,故选B.答案:B2.(2011广东,5分)正五棱柱中,不同在任何侧面且不同在任何底面的两顶点的连线称为它的对角线,那么一个正五棱柱对角线的条数共有()A.20B.15C.12D.10解析:如图,在正五棱柱ABCDE-A1B1C1D1E1中,从顶点A出发的对角线有两条:AC1、AD1,同理从B、C、D、E点出发的对角线也有两条,共2×5=10条.答案:D考点二三视图与直观图1.(2013新课标全国Ⅰ,5分)某几何体的三视图如图所示,则该几何体的体积为()A.16+8πB.8+8πC.16+16πD.8+16π解析:本题考查空间组合体的三视图及组合体的体积计算,意在考查考生的识图能力、空间想象能力以及计算能力.先根据三视图判断出组合体的结构特征,再根据几何体的体积公式进行计算.根据三视图可以判断该几何体由上、下两部分组成,其中上面部分为长方体,下面部分为半个圆柱,所以组合体的体积为2×2×4+π×22×4=16+8π,选择A.答案:A2.(2013山东,5分)一个四棱锥的侧棱长都相等,底面是正方形,其正(主)视图如图所示,则该四棱锥侧面积和体积分别是()A.4,8B.4,C.4(+1),D.8,8解析:本题主要考查三视图的应用,考查空间想象能力和运算能力.由题意可知该四棱锥为正四棱锥,底面边长为2,高为2,侧面上的斜高为=,所以S侧=4×=4,V=×22×2=.答案:B3.(2013浙江,5分)已知某几何体的三视图(单位:cm)如图所示,则该几何体的体积是()A.108cm3B.100cm3C.92cm3D.84cm3解析:本题主要考查考生对三视图与几何体的相互转化的掌握情况,同时考查空间想象能力.根据几何体的三视图可知,所求几何体是一个长方体截去一个三棱锥,∴几何体的体积V=6×6×3-××4×4×3=100cm3.答案:B4.(2013湖南,5分)已知正方体的棱长为1,其俯视图是一个面积为1的正方形,侧视图是一个面积为的矩形,则该正方体的正视图的面积等于()A.B.1C.D.解析:本题主要考查三视图与图形面积的计算,意在考查考生处理问题的能力.由已知,正方体的正视图与侧视图都是长为,宽为1的矩形,所以正视图的面积等于侧视图的面积,为.答案:D5.(2013四川,5分)一个几何体的三视图如图所示,则该几何体可以是()A.棱柱B.棱台C.圆柱D.圆台解析:本题主要考查简单几何体的三视图,意在考查考生数形结合的能力.由俯视图可排除A,B,由正视图可排除C,选D.答案:D6.(2013北京,5分)某四棱锥的三视图如图所示,该四棱锥的体积为________.解析:本题主要考查三视图的相关知识及锥体的体积公式,意在考查考生的运算求解能力,空间想象能力及推理论证能力,解题时先由三视图得到直观图,再进行求解.由三视图可知直观图是一个底面为边长等于3的正方形,高为1的四棱锥,由棱锥的体积公式得V四棱锥=×32×1=3.答案:37.(2013陕西,5分)某几何体的三视图如图所示,则其表面积为________.解析:本题主要考查三视图和空间几何体之间的关系,涉及面积的计算方法.由三视图,易知原几何体是个半球,其半径为1,S=π×12+×4×π×12=3π.答案:3π8.(2012新课标全国,5分)如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则此几何体的体积为()A.6B.9C.12D.18解析:由三视图可知该几何体为底面是斜边为6的等腰直角三角形,高为3的三棱锥,其体积为××6×3...