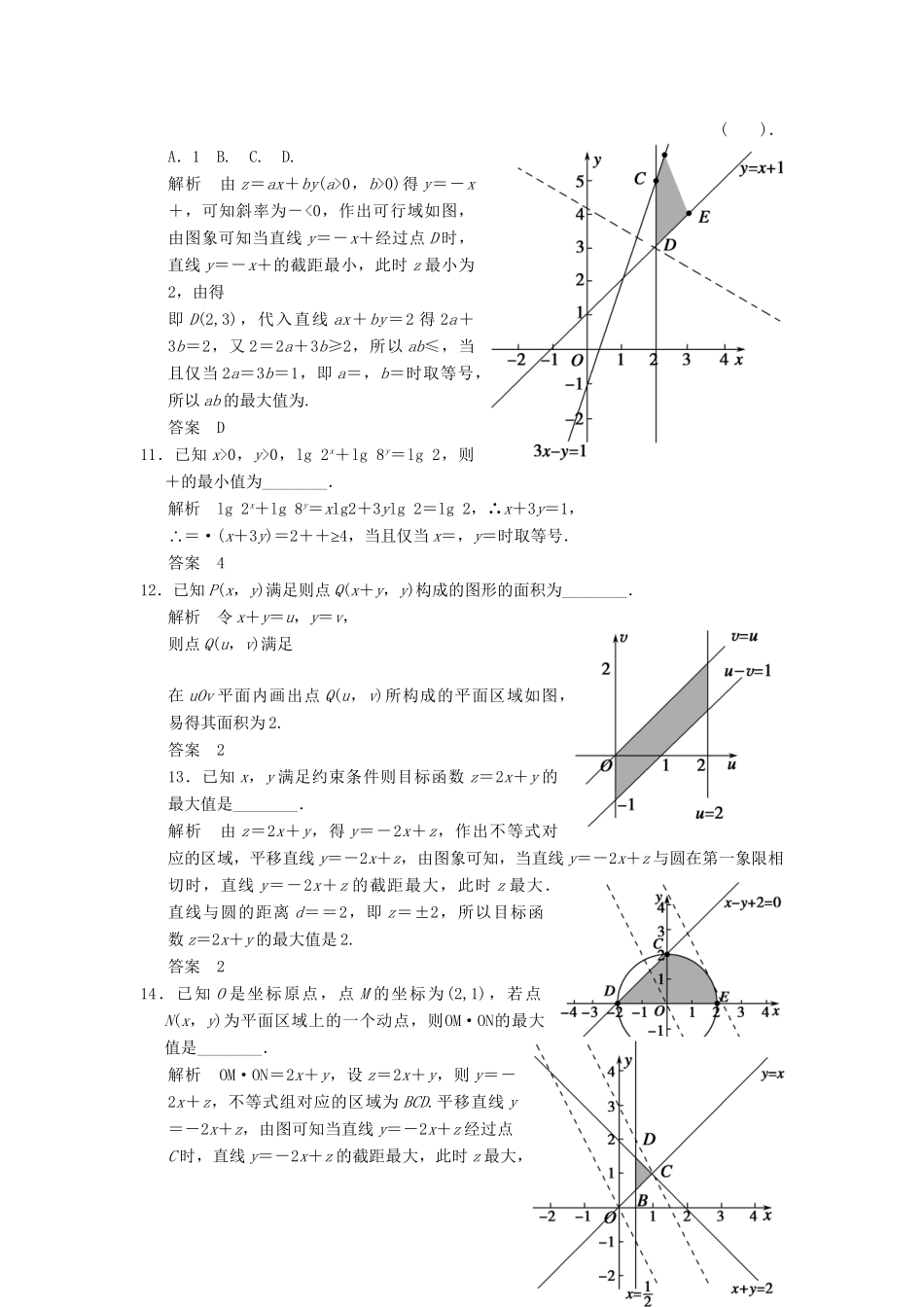
第七辑不等式[通关演练](建议用时:40分钟)1.已知集合A={x∈R|2x+1<0},B={x∈R|(x+1)(x-2)<0},则A∩B=().A.(∞-,-1)B.C.D.(2∞,+)解析A=,B=,所以A∩B=.答案B2.已知集合A=,B={x||x-1|≤1},则A∩B=().A.{-1,0}B.{0,1}C.{0}D.{1}解析A=={0,1,-1},B={x||x-1|≤1}={x|0≤x≤2},所以A∩B={0,1}.答案B3.已知a,b,c是实数,给出下列四个命题:①若a>b,则<;②若a>b,且k∈N*,则ak>bk;③若ac2>bc2,则a>b;④若c>a>b>0,则>.其中正确的命题的序号是().A.①④B.①②④C.③④D.②③解析当a>0>b时,>,故命题①错误;当a>0,b<0,且a<|b|,k是偶数时,命题②错误;当ac2>bc2时,因为c2>0,所以a>b,即命题③正确;对于命题④,因为c>a,所以c-a>0,从而>0,又a>b>0,所以>,故命题④正确.答案C4.设函数f(x)=则不等式f(x)>f(1)的解集是().A.(-3,1)∪(3∞,+)B.(-3,1)∪(2∞,+)C.(-1,1)∪(3∞,+)D.(∞-,-3)∪(1,3)解析由题意知f(1)=3,故原不等式可化为或所以原不等式的解集为(-3,1)∪(3∞,+).答案A5.若正数x,y满足x+3y=5xy,则3x+4y的最小值是().A.B.C.5D.6解析∵x>0,y>0,由x+3y=5xy,得+=5.∴5(3x+4y)=(3x+4y)=13≥++13+2=25.因此3x+4y≥5,当且仅当x=2y时等号成立.∴当x=1,y=时,3x+4y的最小值为5.答案C6.已知实数x,y满足则目标函数z=x-y的最小值为().A.-2B.5C.6D.7解析由z=x-y,得y=x-z.作出不等式对应的平面区域BCD,平移直线y=x-z,由平移可知,当直线y=x-z经过点C时,直线的截距最大,此时z最小.由解得即C(3,5),代入z=x-y得最小值为z=3-5=-2.答案-27.已知不等式|x+2|+|x|≤a的解集不是空集,则实数a的取值范围是().A.(∞-,2)B.(∞-,2]C.(2∞,+)D.[2∞,+)解析因为|x+2|+|x|的最小值为2,所以要使不等式的解集不是空集,则有a≥2.答案D8.已知x,y满足条件(k为常数),若目标函数z=x+3y的最大值为8,则k=().A.-16B.-6C.-D.6解析由z=x+3y得y=-x+,先作出的图象,如图所示,因为目标函数z=x+3y的最大值为8,所以x+3y=8与直线y=x的交点为C,解得C(2,2),代入直线2x+y+k=0,得k=-6.答案B9.设z=x+y,其中实数x,y满足若z的最大值为6,则z的最小值为().A.-3B.-2C.-1D.0解析由z=x+y得y=-x+z,作出的区域BOC,如图所示,平移直线y=-x+z,由图象可知当直线经过C时,直线的截距最大,此时z=6,由解得所以k=3,解得B(-6,3)代入z=x+y的最小值为z=-6+3=-3.答案A10.设x,y满足约束条件若目标函数z=ax+by(a>0,b>0)的最小值为2,则ab的最大值为().A.1B.C.D.解析由z=ax+by(a>0,b>0)得y=-x+,可知斜率为-<0,作出可行域如图,由图象可知当直线y=-x+经过点D时,直线y=-x+的截距最小,此时z最小为2,由得即D(2,3),代入直线ax+by=2得2a+3b=2,又2=2a+3b≥2,所以ab≤,当且仅当2a=3b=1,即a=,b=时取等号,所以ab的最大值为.答案D11.已知x>0,y>0,lg2x+lg8y=lg2,则+的最小值为________.解析lg2x+lg8y=xlg2+3ylg2=lg2,∴x+3y=1,∴=·(x+3y)=2≥++4,当且仅当x=,y=时取等号.答案412.已知P(x,y)满足则点Q(x+y,y)构成的图形的面积为________.解析令x+y=u,y=v,则点Q(u,v)满足在uOv平面内画出点Q(u,v)所构成的平面区域如图,易得其面积为2.答案213.已知x,y满足约束条件则目标函数z=2x+y的最大值是________.解析由z=2x+y,得y=-2x+z,作出不等式对应的区域,平移直线y=-2x+z,由图象可知,当直线y=-2x+z与圆在第一象限相切时,直线y=-2x+z的截距最大,此时z最大.直线与圆的距离d==2,即z=±2,所以目标函数z=2x+y的最大值是2.答案214.已知O是坐标原点,点M的坐标为(2,1),若点N(x,y)为平面区域上的一个动点,则OM·ON的最大值是________.解析OM·ON=2x+y,设z=2x+y,则y=-2x+z,不等式组对应的区域为BCD.平移直线y=-2x+z,由图可知当直线y=-2x+z经过点C时,直线y=-2x+z的截距最大,此时z最大,由解得即C(1,1),代入z=2x+y得z=2x+y=3,所以OM·ON的最大值为3.答案3