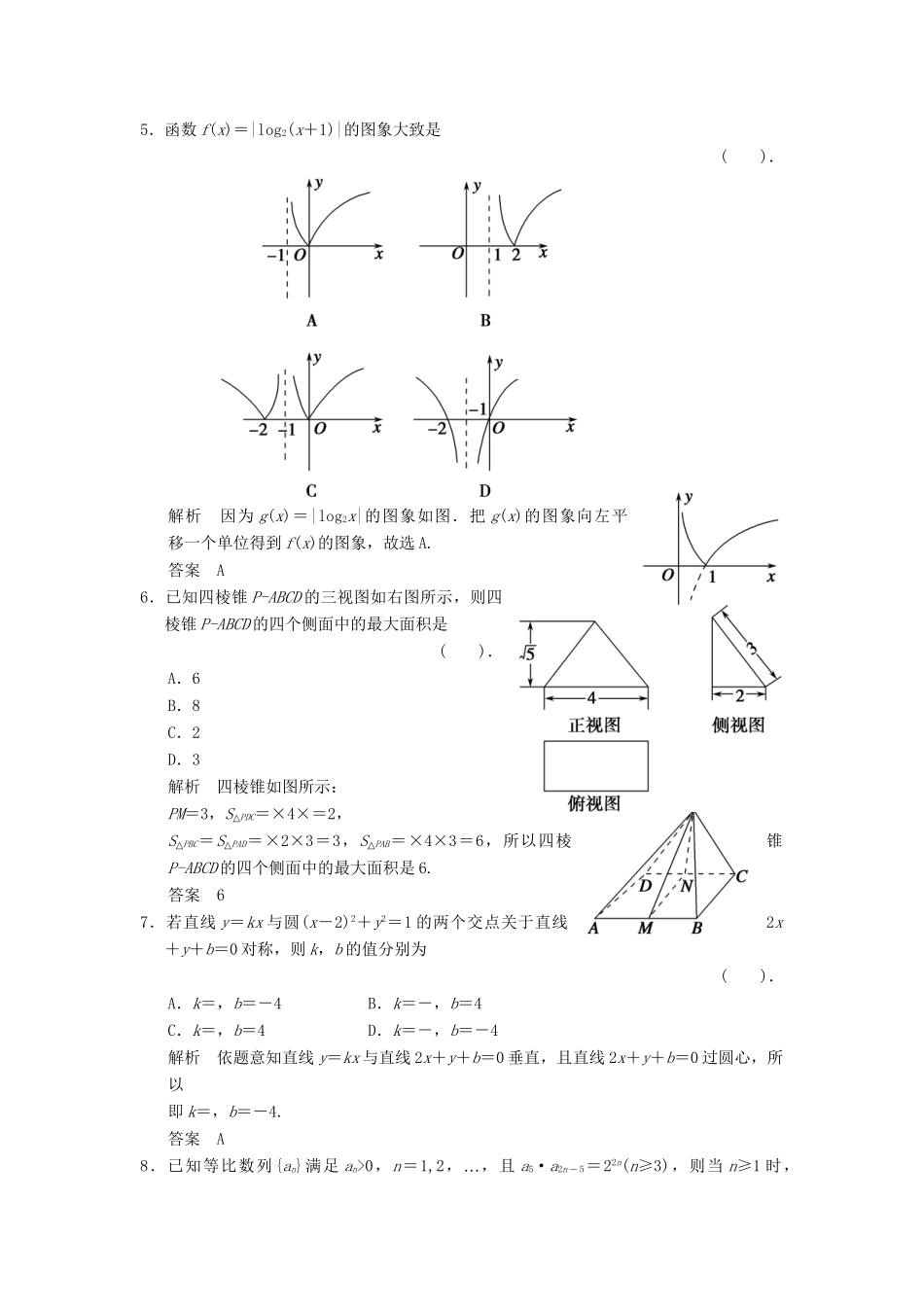
[小题押题练B组](建议用时:40分钟)1.设i是虚数单位,复数是纯虚数,则实数a=().A.-2B.2C.-D.解析==+i,依题意知=0≠,且0,即a=.答案D2.设全集U=R,A={x|2x(x—2)<1},B={x|y=ln(1-x)},则图中阴影部分表示的集合为().A.{x|x≥1}B.{x|1≤x<2}C.{x|00}={x|x<1},∴∁UB={x|x≥1},∴A∩∁UB={x|1≤x<2}.答案B3.下列命题中,真命题是().A“.命题若p,则q”“的否命题是若p,则綈q”B.命题p:∃x∈R,使得x2+1<0,则綈p,∀x∈R,使得x2+1≥0C.已知命题p,q“,若p∨q”为假命题,则命题p与q一真一假D.a+b=0的充要条件是=-1解析A“中,命题若p,则q”“的否命题是若綈p,则綈q”,错误;B正确;C中,若“p∨q”为假,则命题p与q均假,错误;D中,a=b=0时=-1错误.答案B4.某校200名学生期中考试语文成绩的频率分布直方图如图所示,其中成绩分组区间是:[50,60),[60,70),[70,80),[80,90),[90,100].则成绩在[90,100]内的人数为().A.20B.15C.10D.5解析由直方图知[90,100]内的频率为:[1-(0.02+0.03+0.04)×10]=0.05,所以成绩在[90,100]内的人数为:0.05×200=10(人).答案C5.函数f(x)=|log2(x+1)|的图象大致是().解析因为g(x)=|log2x|的图象如图.把g(x)的图象向左平移一个单位得到f(x)的图象,故选A.答案A6.已知四棱锥P-ABCD的三视图如右图所示,则四棱锥P-ABCD的四个侧面中的最大面积是().A.6B.8C.2D.3解析四棱锥如图所示:PM=3,S△PDC=×4×=2,S△PBC=S△PAD=×2×3=3,S△PAB=×4×3=6,所以四棱锥P-ABCD的四个侧面中的最大面积是6.答案67.若直线y=kx与圆(x-2)2+y2=1的两个交点关于直线2x+y+b=0对称,则k,b的值分别为().A.k=,b=-4B.k=-,b=4C.k=,b=4D.k=-,b=-4解析依题意知直线y=kx与直线2x+y+b=0垂直,且直线2x+y+b=0过圆心,所以即k=,b=-4.答案A8.已知等比数列{an}满足an>0,n=1,2…,,且a5·a2n-5=22n(n≥3),则当n≥1时,log2a1+log2a3…++log2a2n-1=().A.n(2n-1)B.(n+1)2C.n2D.(n-1)2解析log2a1+log2a3…++log2a2n-1=log2(a1a3…a2n-1)=log2(a5·a2n-5)=n2.答案C9.已知△ABC内角A,B,C的对边分别是a,b,c,若cosB=,b=2,sinC=2sinA,则△ABC的面积为().A.B.C.D.解析由正弦定理=,得c=2a①由余弦定理b2=a2+c2-2accosB,得4=a2+c2-2ac×②由①②得:a=1,c=2,又sinB==.所以S△ABC=acsinB=×1×2×=.答案B10.已知函数f(x)=x3-12x+a,其中a≥16,则下列说法正确的是().A.f(x)有且只有一个零点B.f(x)至少有两个零点C.f(x)最多有两个零点D.f(x)一定有三个零点解析f′(x)=3x2-12,令f′(x)>0得x>2或x<-2,令f′(x)<0得-2