[小题押题练D组](建议用时:40分钟)1.设集合A={x|2x≤4},集合B为函数y=lg(x-1)的定义域,则A∩B=().A.(1,2)B.[1,2]C.[1,2)D.(1,2]解析A={x|x≤2},B={x|x>1},∴A∩B={x|1
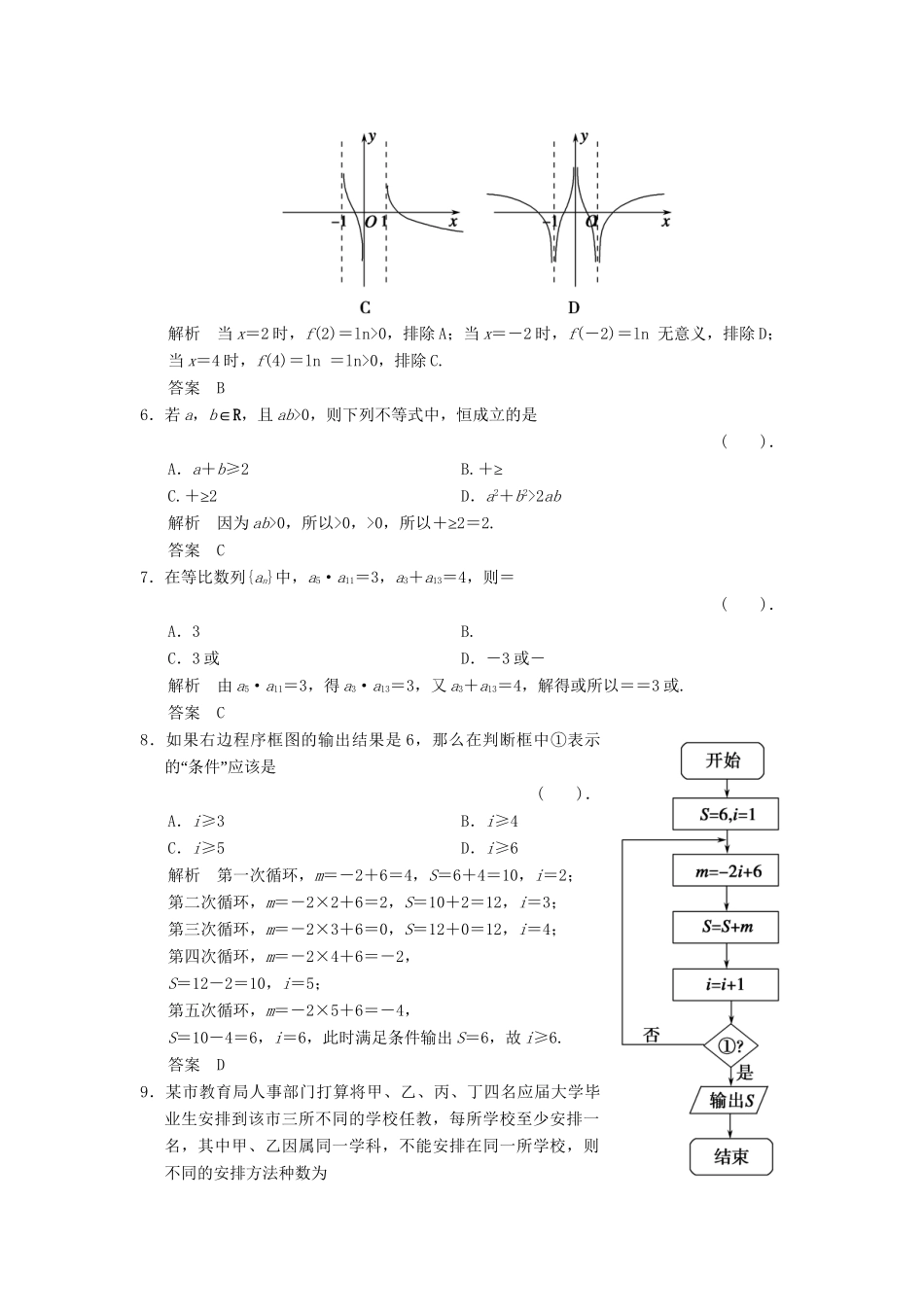
2C.>5,s2<2D.>5,s2>2解析==5,s2==<2.答案A5.函数f(x)=ln的图象是().解析当x=2时,f(2)=ln>0,排除A;当x=-2时,f(-2)=ln无意义,排除D;当x=4时,f(4)=ln=ln>0,排除C.答案B6.若a,b∈R,且ab>0,则下列不等式中,恒成立的是().A.a+b≥2B.≥+C.≥+2D.a2+b2>2ab解析因为ab>0,所以>0,>0≥,所以+2=2.答案C7.在等比数列{an}中,a5·a11=3,a3+a13=4,则=().A.3B.C.3或D.-3或-解析由a5·a11=3,得a3·a13=3,又a3+a13=4,解得或所以==3或.答案C8.如果右边程序框图的输出结果是6,那么在判断框中①表示“”的条件应该是().A.i≥3B.i≥4C.i≥5D.i≥6解析第一次循环,m=-2+6=4,S=6+4=10,i=2;第二次循环,m=-2×2+6=2,S=10+2=12,i=3;第三次循环,m=-2×3+6=0,S=12+0=12,i=4;第四次循环,m=-2×4+6=-2,S=12-2=10,i=5;第五次循环,m=-2×5+6=-4,S=10-4=6,i=6,此时满足条件输出S=6,故i≥6.答案D9.某市教育局人事部门打算将甲、乙、丙、丁四名应届大学毕业生安排到该市三所不同的学校任教,每所学校至少安排一名,其中甲、乙因属同一学科,不能安排在同一所学校,则不同的安排方法种数为().A.18B.24C.30D.36解析四名学生中有两名分在一所学校的种数是C,顺序有A种,而甲、乙被分在同一所学校的有A种,故不同的安排方法种数是CA-A=30.答案C10.函数f(x)=Asin(ωx+φ)(其中A>0,|φ|<)的图象如图所示,为了得到g(x)=sin3x的图象,只需将f(x)的图象().A.向右平移个单位长度B.向左平移个单位长度C.向右平移个单位长度D.向左平移个单位长度解析由图象可知A=1,=-=,即T==,所以ω=3,所以f(x)=sin(3x+φ),又f=sin=sin=-1,所以+φ=+2kπ,k∈Z,即φ=+2kπ,k∈Z,又|φ|<所以φ=,即f(x)=sin,又g(x)=sin3x=sin=sin,所以只需将f(x)的图象向右平移个单位长度,即可得到g(x)=sin3x的图象.答案C11.在区间[1,5]和[2,4]分别取一个数,记为a,b,则方程+=1表示焦点在x轴上且离心率小于的椭圆的概率为().A.B.C.D.解析依题意知,a>b,e==<,即b>.如图所示故所求概率为P=1--=1--=.答案B12.定义在R上的奇函数f(x),当x≥0时,f(x)=则关于x的函数F(x)=f(x)-a(0