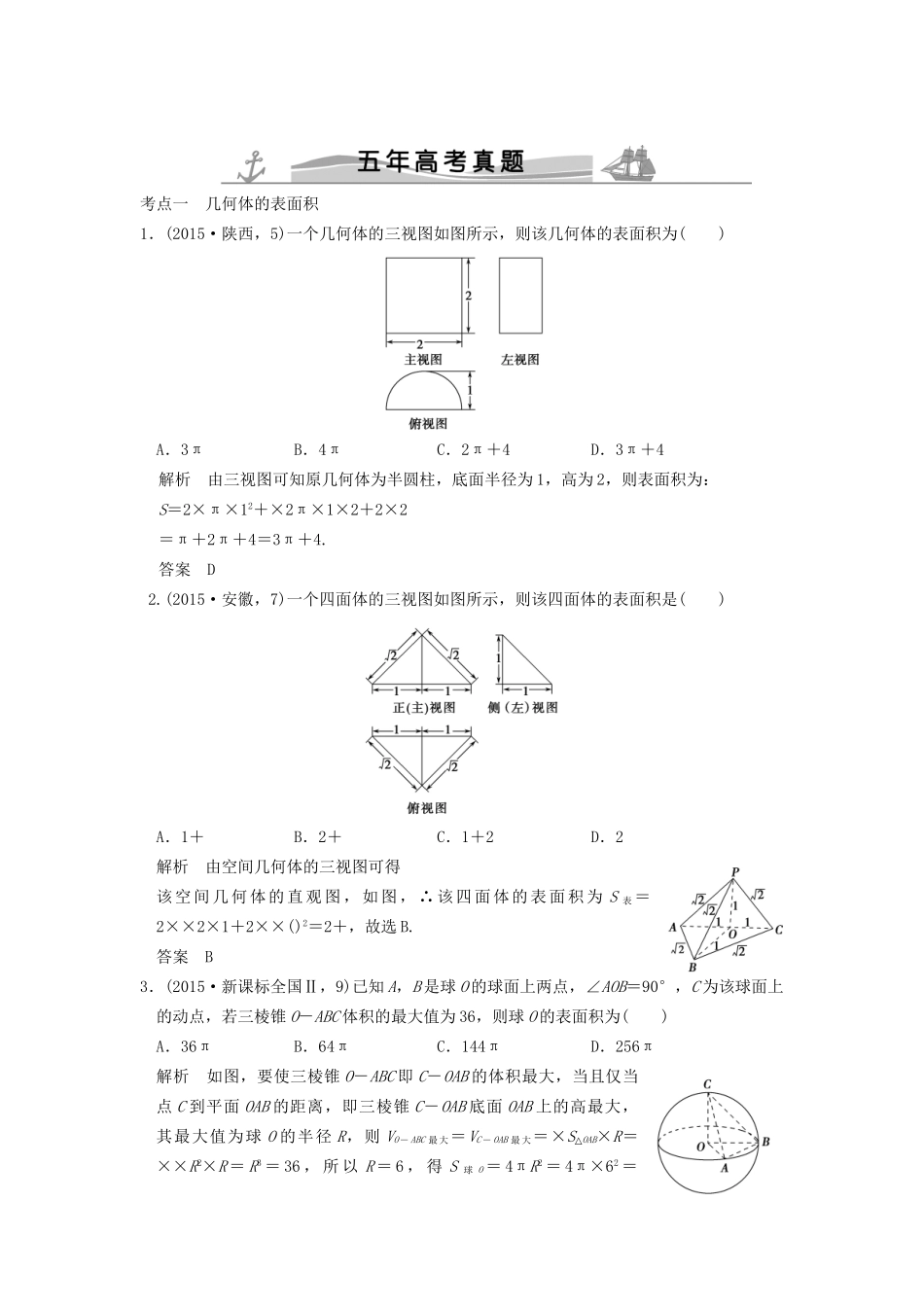
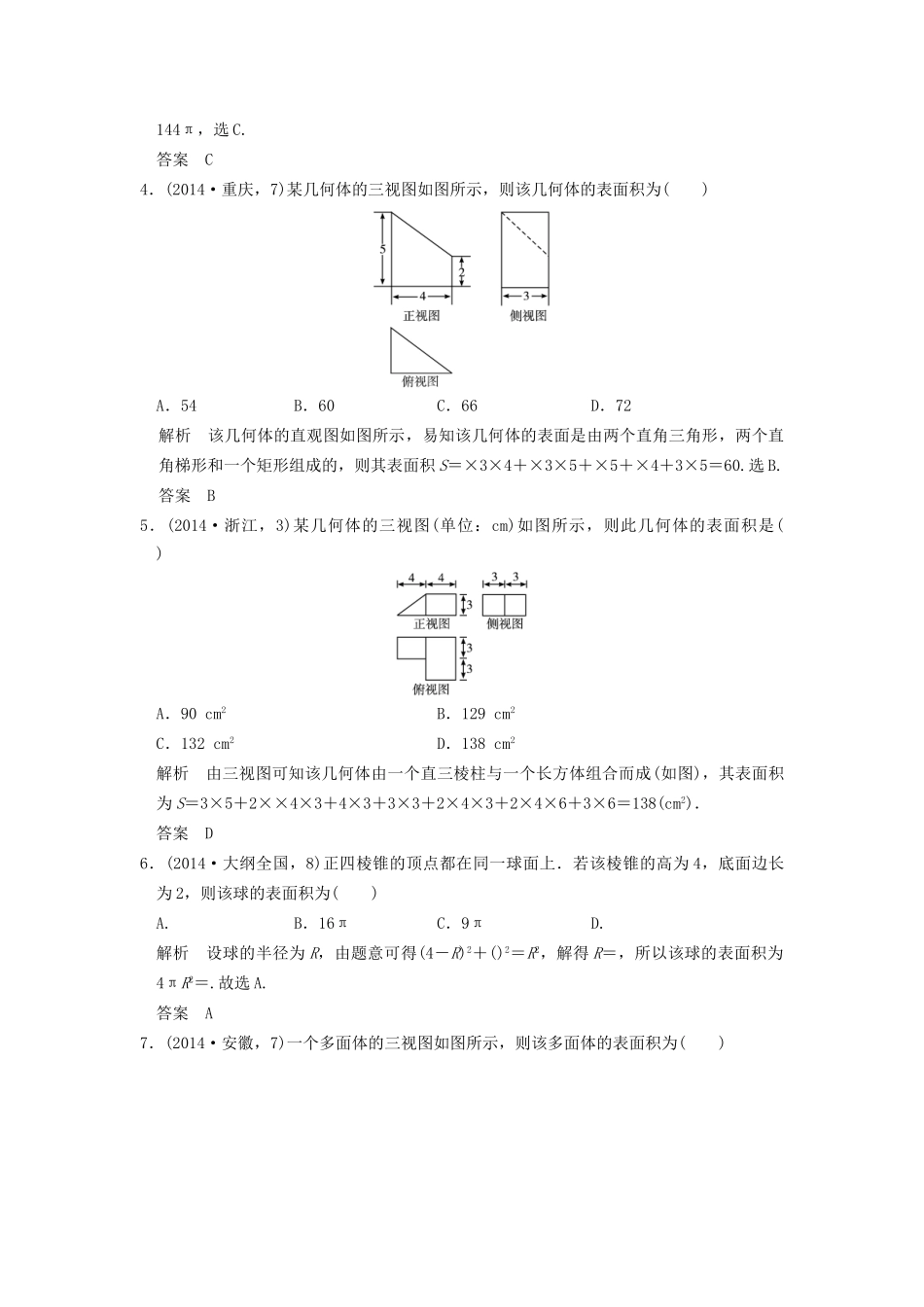
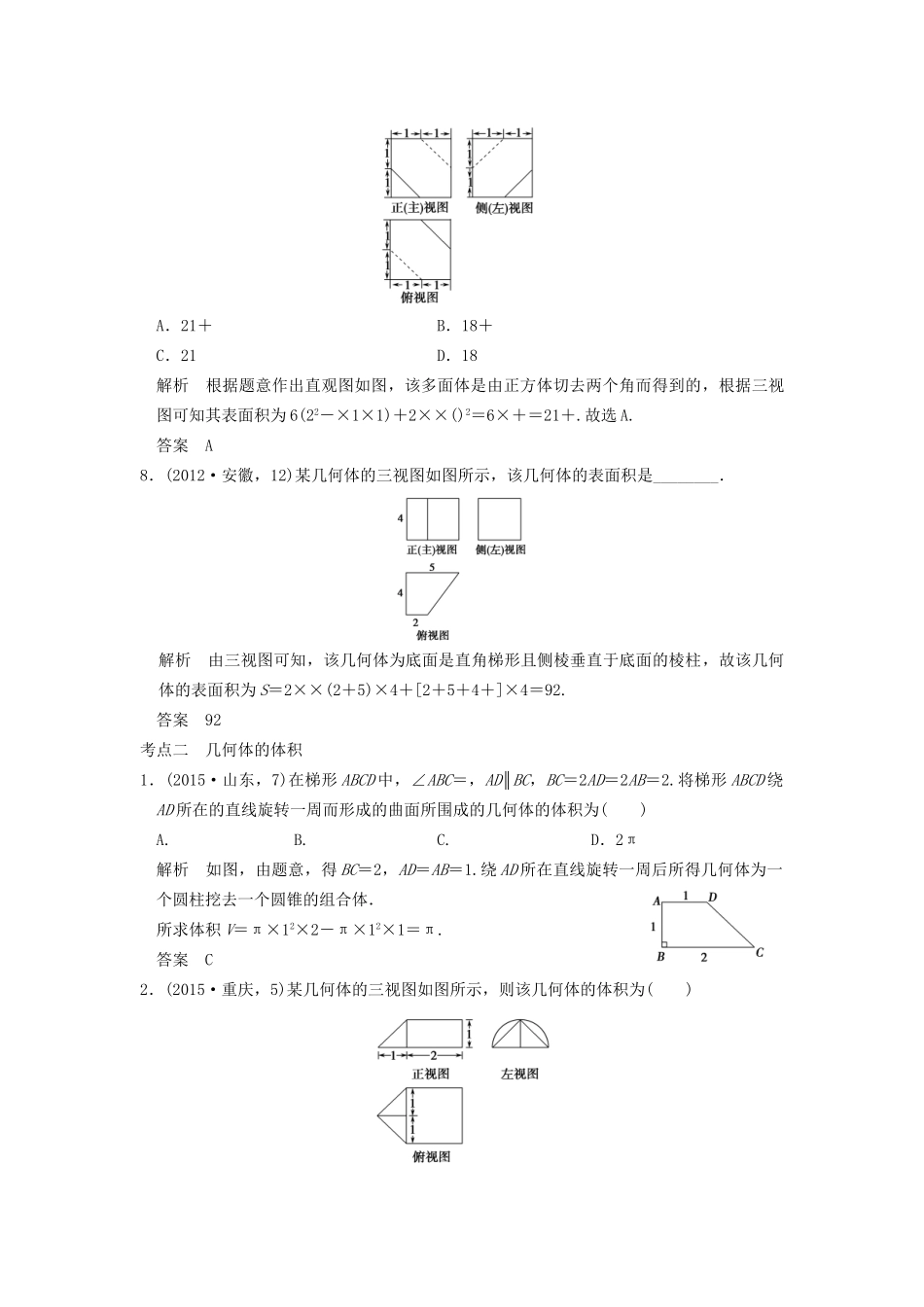
考点一几何体的表面积1.(2015·陕西,5)一个几何体的三视图如图所示,则该几何体的表面积为()A.3πB.4πC.2π+4D.3π+4解析由三视图可知原几何体为半圆柱,底面半径为1,高为2,则表面积为:S=2×π×12+×2π×1×2+2×2=π+2π+4=3π+4.答案D2.(2015·安徽,7)一个四面体的三视图如图所示,则该四面体的表面积是()A.1+B.2+C.1+2D.2解析由空间几何体的三视图可得该空间几何体的直观图,如图,∴该四面体的表面积为S表=2××2×1+2××()2=2+,故选B.答案B3.(2015·新课标全国Ⅱ,9)已知A,B是球O的球面上两点,∠AOB=90°,C为该球面上的动点,若三棱锥O-ABC体积的最大值为36,则球O的表面积为()A.36πB.64πC.144πD.256π解析如图,要使三棱锥O-ABC即C-OAB的体积最大,当且仅当点C到平面OAB的距离,即三棱锥C-OAB底面OAB上的高最大,其最大值为球O的半径R,则VO-ABC最大=VC-OAB最大=×S△OAB×R=××R2×R=R3=36,所以R=6,得S球O=4πR2=4π×62=144π,选C.答案C4.(2014·重庆,7)某几何体的三视图如图所示,则该几何体的表面积为()A.54B.60C.66D.72解析该几何体的直观图如图所示,易知该几何体的表面是由两个直角三角形,两个直角梯形和一个矩形组成的,则其表面积S=×3×4+×3×5+×5+×4+3×5=60.选B.答案B5.(2014·浙江,3)某几何体的三视图(单位:cm)如图所示,则此几何体的表面积是()A.90cm2B.129cm2C.132cm2D.138cm2解析由三视图可知该几何体由一个直三棱柱与一个长方体组合而成(如图),其表面积为S=3×5+2××4×3+4×3+3×3+2×4×3+2×4×6+3×6=138(cm2).答案D6.(2014·大纲全国,8)正四棱锥的顶点都在同一球面上.若该棱锥的高为4,底面边长为2,则该球的表面积为()A.B.16πC.9πD.解析设球的半径为R,由题意可得(4-R)2+()2=R2,解得R=,所以该球的表面积为4πR2=.故选A.答案A7.(2014·安徽,7)一个多面体的三视图如图所示,则该多面体的表面积为()A.21+B.18+C.21D.18解析根据题意作出直观图如图,该多面体是由正方体切去两个角而得到的,根据三视图可知其表面积为6(22-×1×1)+2××()2=6×+=21+.故选A.答案A8.(2012·安徽,12)某几何体的三视图如图所示,该几何体的表面积是________.解析由三视图可知,该几何体为底面是直角梯形且侧棱垂直于底面的棱柱,故该几何体的表面积为S=2××(2+5)×4+[2+5+4+]×4=92.答案92考点二几何体的体积1.(2015·山东,7)在梯形ABCD中,∠ABC=,AD∥BC,BC=2AD=2AB=2.将梯形ABCD绕AD所在的直线旋转一周而形成的曲面所围成的几何体的体积为()A.B.C.D.2π解析如图,由题意,得BC=2,AD=AB=1.绕AD所在直线旋转一周后所得几何体为一个圆柱挖去一个圆锥的组合体.所求体积V=π×12×2-π×12×1=π.答案C2.(2015·重庆,5)某几何体的三视图如图所示,则该几何体的体积为()A.+πB.+πC.+2πD.+2π解析这是一个三棱锥与半个圆柱的组合体,V=π×12×2+××1=π+,选A.答案A3.(2015·新课标全国Ⅱ,6)一个正方体被一个平面截去一部分后,剩余部分的三视图如图所示,则截去部分体积与剩余部分体积的比值为()A.B.C.D.解析如图,由题意知,该几何体是正方体ABCD-A1B1C1D1被过三点A、B1、D1的平面所截剩余部分,截去的部分为三棱锥A-A1B1D1,设正方体的棱长为1,则截去部分体积与剩余部分体积的比值为===,选D.答案D4.(2015·湖南,10)某工件的三视图如图所示,现将该工件通过切削,加工成一个体积尽可能大的长方体新工件,并使新工件的一个面落在原工件的一个面内,则原工件材料的利用率为(材料利用率=)()A.B.C.D.解析易知原工件为一圆锥,V1=πr2h=π,设内接长方体长、宽、高为a、b、c,欲令体积最大,则a=b.由截面图的相似关系知,c+=2,即c+a=2,∴V长方体=abc=a2c=a2(2-a),设g(a)=2a2-a3,则g′(a)=4a-3a=0,令g′(a)=0,解得a=,所以令a=时,V长方体最大为,∴==.故选A.答案A5.(2014·陕西,5)已知底面边长为1,侧棱长为的正四棱柱的各顶点均在同一个球面上,则该球的体...