正弦定理 ()VIP免费

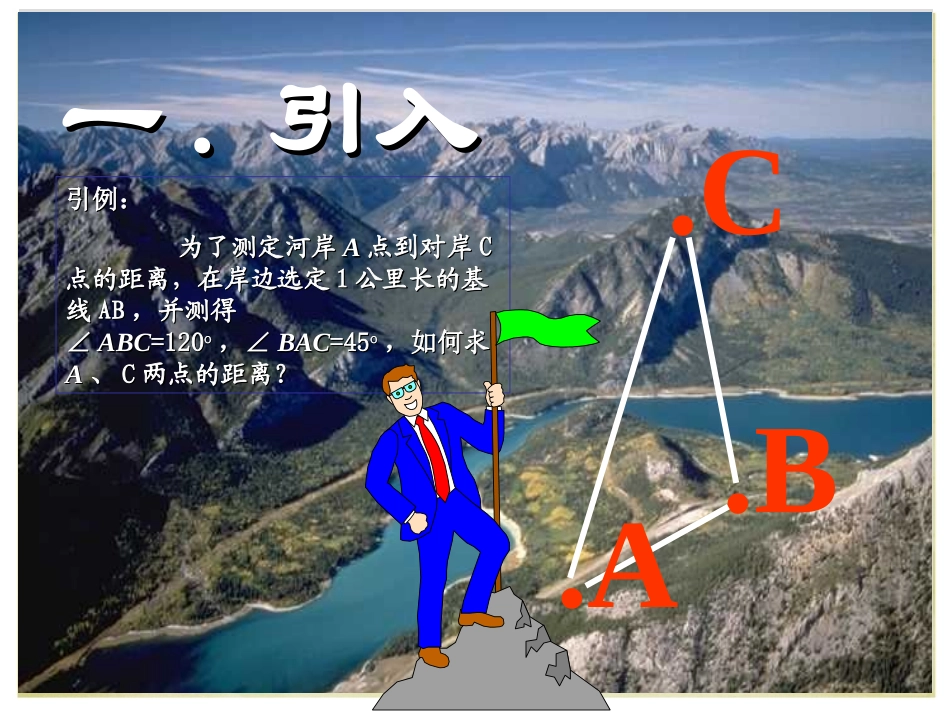
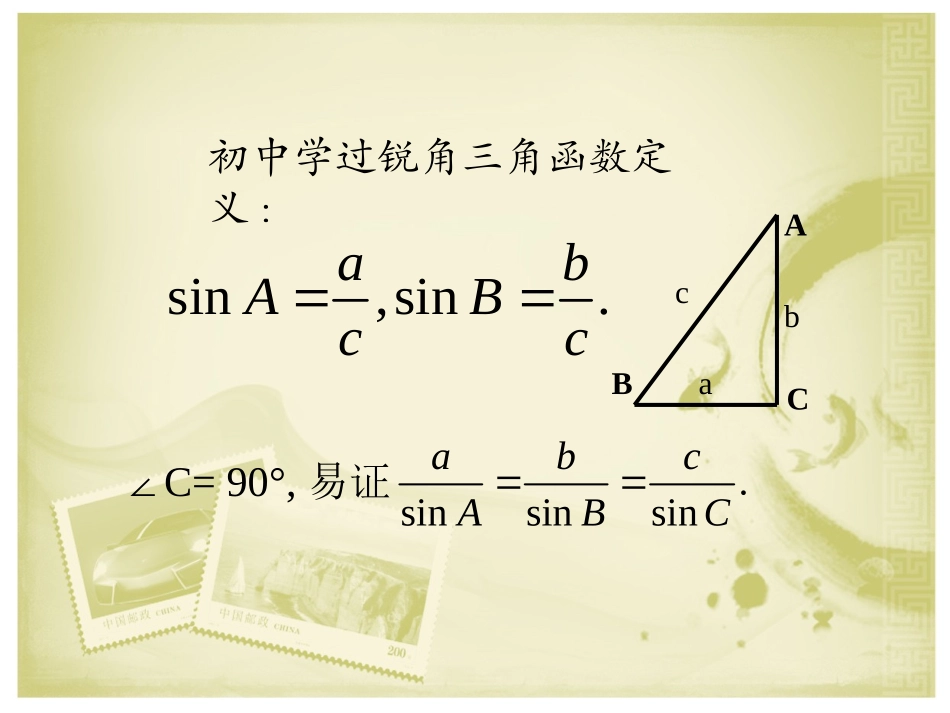
1.1.1正弦定理一一..引入引入.C.B.A引例：引例：为了测定河岸为了测定河岸AA点到对岸点到对岸CC点的距离，在岸边选定点的距离，在岸边选定11公里长的基公里长的基线线ABAB，，并测得并测得∠∠ABCABC=120=120oo，∠，∠BACBAC=45=45oo，如何，如何求求AA、、CC两点的距离？两点的距离？sin,sin.abABcc初中学过锐角三角函数定义:∠C=90°,易证.sinsinsinabcABCBCAcba2．能否推广到斜三角形？证明一证明二（面积法）在任意斜△ABC当中：AbcBacCabSABCsin21sin21sin21两边同除以abc21即得：.sinsinsinCcBbAa3．用向量证明：证明三：过A作单位向量垂直于同理：若过C作,ACACCBAB两边同乘以,jACCBABjjjcos90cos(90)cos(90)ooojACjCBCjABA��AcCasinsin垂直于jCB得jACB图.sinsinCcBb.sinsinCcAa为钝角三角形时，设A>90过A作单位向量j垂直于向量,ACjACB图则j与,AB的夹角为A-90,j与,BC的夹角为90-C.同样可证得这就是说，对于锐角三角形、直角三角形、钝角三角形来说，上面的关系式均成立.因此.我们得到下面的定理..sinsinsinCcBbAa证法四：（用几何法证明）即证二.正弦定理在一个三角形中，各边和它所对角的正弦的比相等，即.sinsinsinCcBbAa1正弦定理的叙述：在一个三角形中。各边和它所对角的正弦比相等，即：它适合于任何三角形.2灵活应用（R为△ABC外接圆半径）3每个等式可视为一个方程：知三求一..sinsinsinCcBbAa.2sinsinsinRCcBbAa三、正弦定理的应用从理论上正弦定理可解决两类问题：1．两角和任意一边，求其它两边和一角；2．两边和其中一边对角，求另一边的对角，进而可求其它的边和角。例1在△ABC中，已知10,cA=45,C=30,求b（保留两个有效数字）..sinsin7().12710sinsin1219.sinsin6bcBCBACcBbC解：由例2在△ABC中，已知b=28,A=40,求B(精确到1)和c（保留两个有效数字）.20,a0sin28sin40sin0.899920bABa解：001264,116.BB.76)4064(180)(180,64000010101ABCB时当.3040sin76sin20sinsin0011ACac.24)40116(180)(180,116000020202ABCB时当.1340sin24sin20sinsin0022ACac例3在△ABC中，已知60,ab=50,A=38,求B(精确到1)和c（保留两个有效数字）.解：已知bb一解a≤b无解ＡＢＣbaＡＣbaＡＣabＡＢＣabＡＢ１Ｂ２ＣabＡＢＣab