信号与系统考题参考解答(完整版) VIP免费

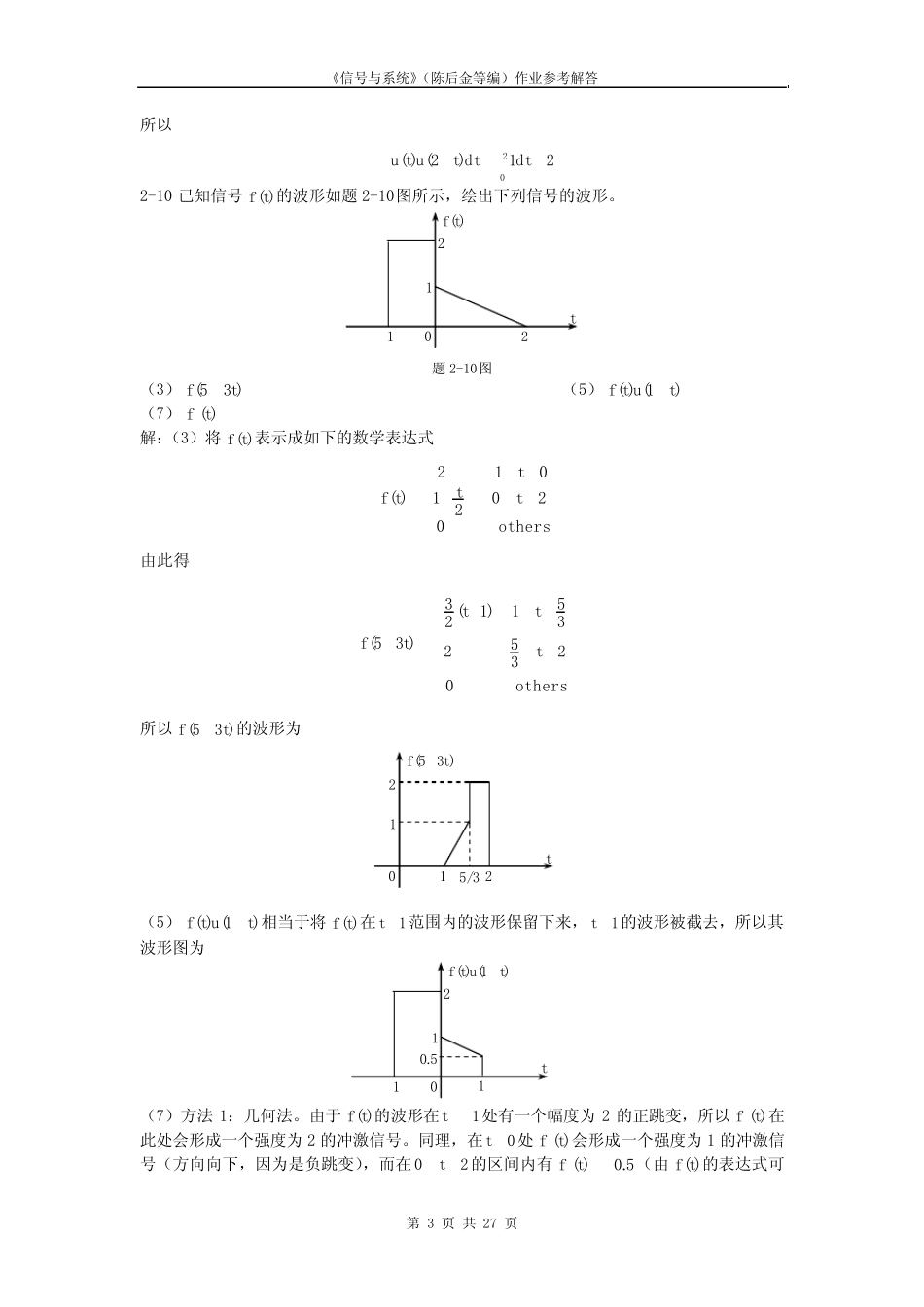
《信号与系统》（陈后金等编）作业参考解答第1页共27页《信号与系统》作业参考解答第一章（P16-17）1-3设)(1tf和)(2tf是基本周期分别为1T和2T的周期信号。证明)()()(21tftftf是周期为T的周期信号的条件为TnTmT21（m,n为正整数）解：由题知)()(111tfmTtf)()(222tfmTtf要使)()()()()(2121tftfTtfTtfTtf则必须有21nTmTT（m,n为正整数）1-5试判断下列信号是否是周期信号。若是，确定其周期。（1）tttfsin62sin3)(（2）2)sin()(tatf（8）2cos28sin4cos)(kkkkf解：（1）因为t2sin的周期为，而tsin的周期为2。显然，使方程nm2（m,n为正整数）成立的正整数m,n是不存在的，所以信号tttfsin62sin3)(是非周期信号。（2）因为)2cos1(2)sin()(22tatatf所以信号2)sin()(tatf是周期T的周期信号。（8）由于)4/cos(k的周期为8)4//(21N，)8/sin(k的周期为16)8//(22N，)2/cos(k的周期为4)2//(23N，且有16412321NNN所以，该信号是周期16N的周期信号。1-10判断下列系统是否为线性时不变系统，为什么？其中)(tf、][kf为输入信号，)(ty、][ky为零状态响应。（1）)()()(tftgty（2）)()()(2tftKfty解：（1）显然，该系统为线性系统。因为)()()()()()(00000ttfttgttyttftgttfT所以该系统为线性时变系统。（注意：该系统方程表达式中)(tf的系数为)(tg，是随时间变化的，所以该系统是时变系统）《信号与系统》（陈后金等编）作业参考解答第2页共27页（2）显然，该系统为非线性系统。由于)()()()(00200ttyttfttKfttfT所以该系统为非线性时不变系统。（注意：该系统方程表达式中)(tf的系数均为常数，不随时间变化，所以该系统是非时变系统）第二章（P55-58）2-2定性绘出下列信号的波形，其中t。（1）)3()()(tututf（4）)1()4()(42teetftt（5）)()2()(tuttf解：（1）其波形图如下（4）由单位冲激信号的筛选特性可得)1(523.0)1()4()(42tteetf所以其波形图如下（5）其波形图如下2-7计算下列积分的值。（2）242)3(dtett（10）dttutu)2()(解：（2）冲激信号)3(t出现的时刻为3t，包含在积分区间内。由冲激信号的取样特性可得6)3(2242)3(eedtett（10）显然，被积函数)2()(tutu在区间]2,0[内的值为1，在其它区间范围内的值均为0。013t)(tf01t)(tf)523.0(02t)(tf2《信号与系统》（陈后金等编）作业参考解答第3页共27页所以2021)2()(dtdttutu2-10已知信号)(tf的波形如题2-10图所示，绘出下列信号的波形。题2-10图（3）)35(tf（5）)1()(tutf（7）)(tf解：（3）将)(tf表示成如下的数学表达式othersttttf02021012)(由此得othersttttf02352351)1(23)35(所以)35(tf的波形为（5）)1()(tutf相当于将)(tf在1t范围内的波形保留下来，1t的波形被截去，所以其波形图为（7）方法1：几何法。由于)(tf的波形在1t处有一个幅度为2的正跳变，所以)(tf在此处会形成一个强度为2的冲激信号。同理，在0t处)(tf会形成一个强度为1的冲激信号（方向向下，因为是负跳变），而在20t的区间内有5.0)(tf（由)(tf的表达式可0t)(tf22110t)35(tf22113/50t)1()(tutf12115.0《信号与系统》（陈后金等编）作业参考解答第4页共27页得）。所以，)(tf的波形为方法2：解析法。由)(tf的波形图可得)]2()()[5.01()]()1([2)(tututtututf所以有)]2()([5.0)()1(2)()]2()([5.0)(2)1(2)2()5.01()()5.01()]2()([5.0)(2)1(2)]2()()[5.01()]2()([5.0)]()1([2)(tututtttututttttttututtttttututttf由此即可得到上面的波形图。（注：在上式中用到了冲激信号的筛选特性）2-18一个离散时间信号)(kf如题...