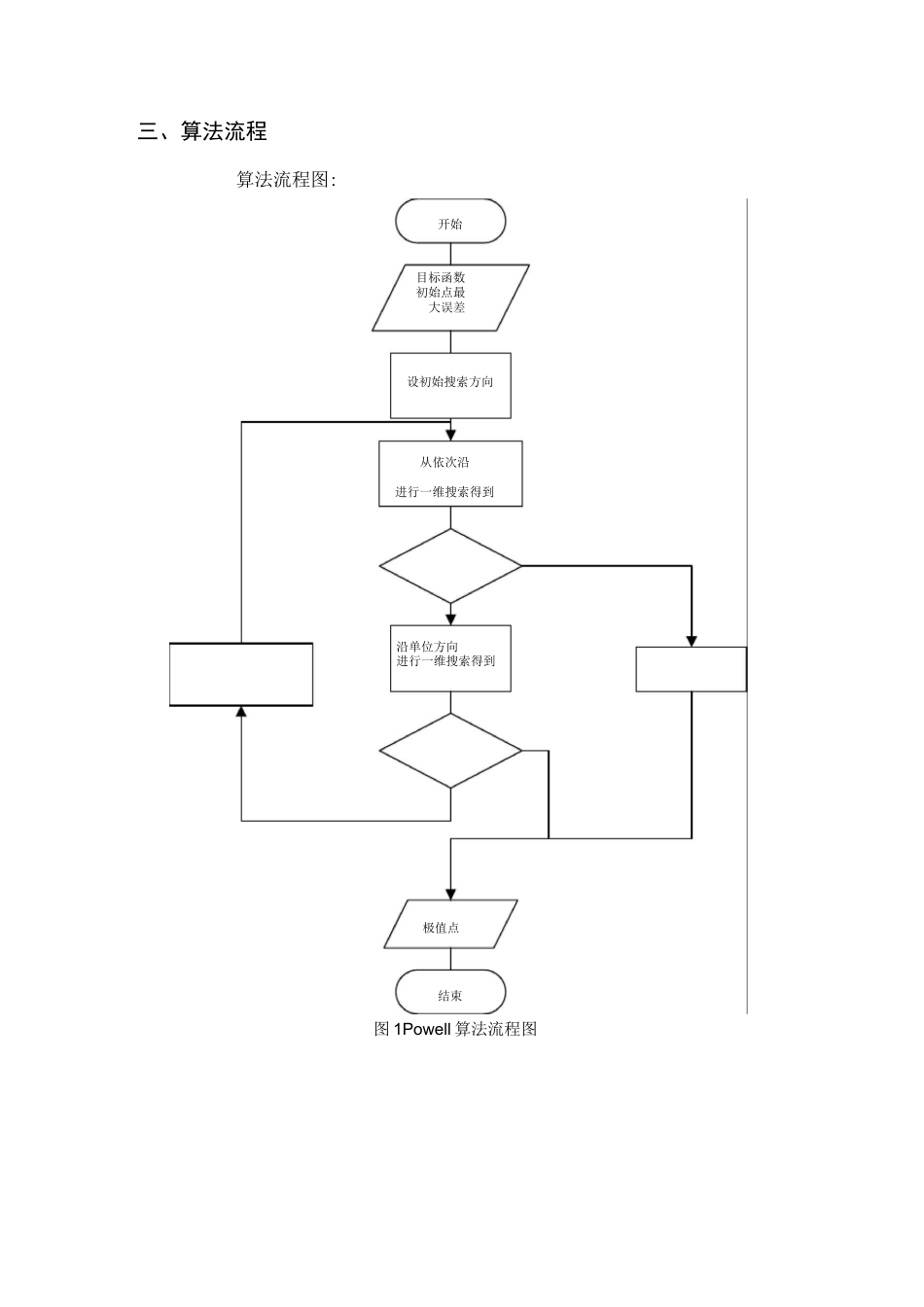
任课教师签字:课程作业学年学期:2017——2018学年第二学期课程名称:优化理论作业名称:作业三学生姓名:号:提交时间:一、问题重述形如的minf(x),xeRn问题称为无约束优化问题,常用下降算法来解决这类问题。下降算法的关键在于步长和搜索方向的选取。步长的求取可以借助前面作业中提到的一维搜索等方法求取,而搜索方向算法可以分为两大类,解析法和直接法。解析法借助了目标函数的导数进行搜索,这类算法搜索速度快、效率高,但是对目标函数的要求更为严格。常用的方法有最速下降法、法、共轭梯度法、拟法等。直接法不使用导数,也不需要得到目标函数的明确解析式,只需要能够得到某些函数上的点即可。因此直接法的适用范围更广,但相应的收敛速度会较慢,计算量也会随着问题维数的增加而迅速增大。常用的方法有单纯形法、方向加速法以及改进算法。本作业以直接法的法为例,解决具体的无约束优化问题,并对将方向加速法和改进算法解决结果进行对比。二、算法原理对于维正定二次函数f(x)=0.5XTGX+bTx+c,设p,pp(k