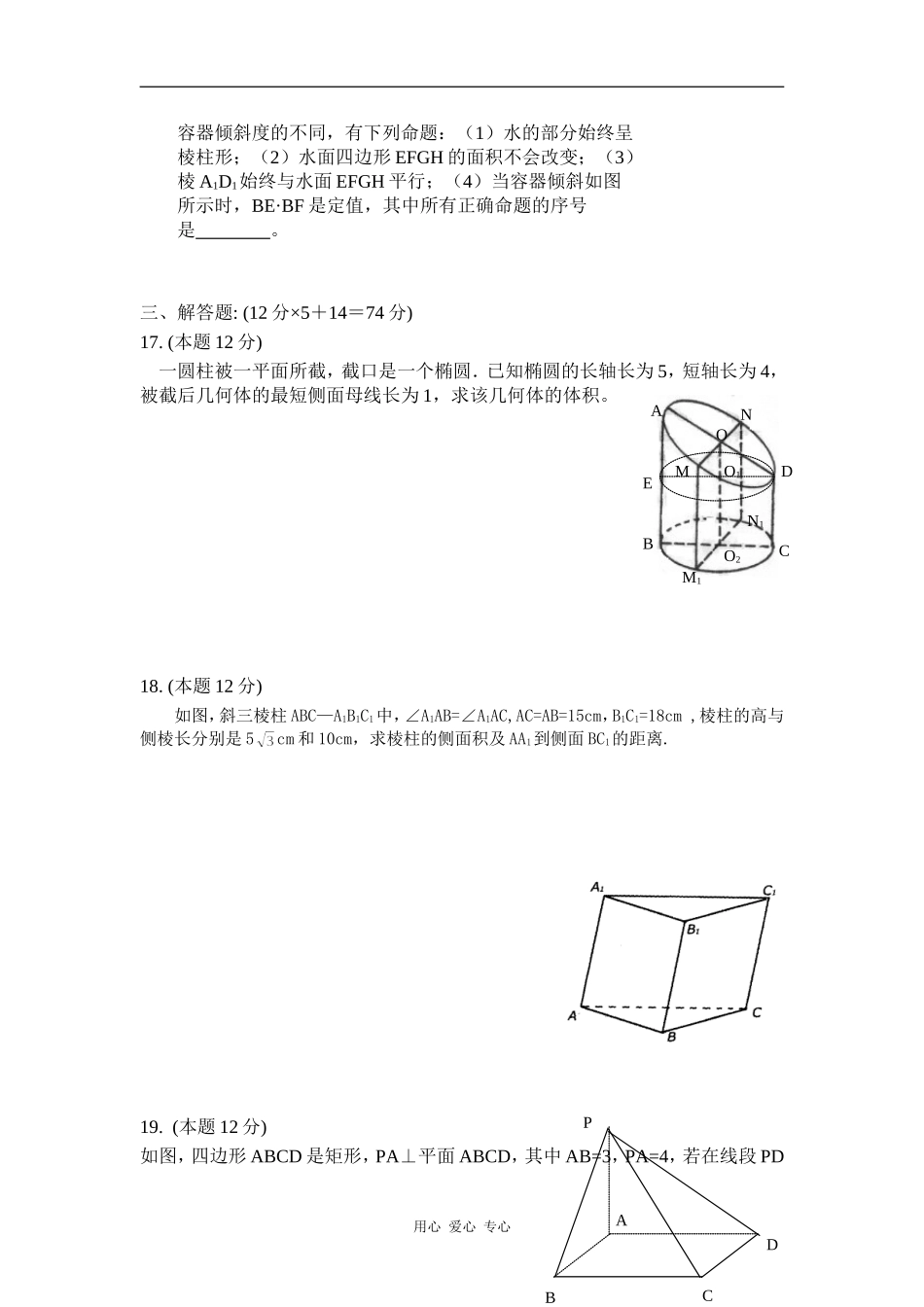
高考一轮专练——简单几何体一、选择题:(每题5分,共60分)1.用一个平面去截正方体,所得的截面不可能是()(A)六边形(B)菱形(C)梯形(D)直角三角形2.已知一个简单多面体的各个顶点处都有三条棱,则顶点数V与面数F满足的关系式是()(A)2F+V=4(B)2F-V=4(C)2F+V=2(D)2F-V=23.直三棱柱ABC-A1B1C1的体积为V,点P、Q分别在侧棱AA1和CC1上,AP=C1Q,则四棱锥B-APQC的体积为()(A)(B)(C)(D)4.已知三棱锥D-ABC的三个侧面与底面全等,且AB=AC=,BC=2,则以BC为棱,以面BCD与面BCA为面的二面角的大小是()(A)(B)(C)(D)5.斜棱柱底面和侧面中矩形的个数最多可有()(A)2个(B)3个(C)4个(D)6个6.已知球面的三个大圆所在平面两两垂直,则以三个大圆的交点为顶点的八面体的体积与球体积之比是()(A)2∶π(B)1∶2π(C)1∶π(D)4∶3π7.如图,在斜三棱柱A1B1C1-ABC中,∠BAC=900,BC1⊥AC,则C1在底面ABC上的射影H必在()(A)直线AB上(B)直线BC上(C)直线AC上(D)△ABC内部(第7题图)(第8题图)8.在棱长为a的正方体ABCD-A1B1C1D1中,P,Q是对角线A1C上的点,且PQ=,则三棱锥P-BDQ的体积为()(A)(B)(C)(D)无法确定9.已知球的内接三棱锥的三条侧棱两两垂直,长度分别为3cm,2cm和cm,则此球的体积为()用心爱心专心(A)(B)(C)(D)10.如图,在一根长11cm,外圆周长6cm的圆柱形柱体外表面,用一根细铁丝缠绕,组成10个螺旋,如果铁丝的两端恰好落在圆柱的同一条母线上,则铁丝长度的最小值为()(A)61cm(B)cm(C)cm(D)10cm11.已知四棱锥P-ABCD的底面为平行四边形,设x=2PA2+2PC2-AC2,y=2PB2+2PD2-BD2,则x,y之间的关系为()(A)x>y(B)x=y(C)x<y(D)不能确定12.如图,三棱柱ABC-A1B1C1的侧面A1B⊥BC,且A1C与底面成600角,AB=BC=2,则该棱柱体积的最小值为()(A)(B)(C)4(D)3二、填空题:(每题4分,共16分)13.球面上有3个点,其中任意两点的球面距离都等于大圆周长的,经过这3点的小圆的周长为4,那么这个球的半径为_____________14.如图,在四棱锥P-ABCD中,E为CD上的动点,四边形ABCD为时,体积VP-AEB恒为定值(写上你认为正确的一个答案即可).(第14题图)(第15题图)15.如图,在四棱锥E-ABCD中,底面ABCD为梯形,AB∥CD,2AB=3DC,M为AE的中点,设E-ABCD的体积为V,则三棱锥M-EBC的体积为.16.如图,在透明材料制成的长方体容器ABCD—A1B1C1D1内灌注一些水,固定容器底面一边BC于桌面上,再将用心爱心专心D1B1A1DAFECC1B容器倾斜度的不同,有下列命题:(1)水的部分始终呈棱柱形;(2)水面四边形EFGH的面积不会改变;(3)棱A1D1始终与水面EFGH平行;(4)当容器倾斜如图所示时,BE·BF是定值,其中所有正确命题的序号是。三、解答题:(12分×5+14=74分)17.(本题12分)一圆柱被一平面所截,截口是一个椭圆.已知椭圆的长轴长为5,短轴长为4,被截后几何体的最短侧面母线长为1,求该几何体的体积。18.(本题12分)如图,斜三棱柱ABC—A1B1C1中,∠A1AB=∠A1AC,AC=AB=15cm,B1C1=18cm,棱柱的高与侧棱长分别是5cm和10cm,求棱柱的侧面积及AA1到侧面BC1的距离.19.(本题12分)如图,四边形ABCD是矩形,PA⊥平面ABCD,其中AB=3,PA=4,若在线段PD用心爱心专心PBCADABCDEOO2O1MNM1N1上存在点E使得BE⊥CE,求线段AD的取值范围,并求当线段PD上有且只有一个点E使得BE⊥CE时,二面角E—BC—A的大小。20.(本题12分)如图,正三棱柱的底面边长为a,点M在边BC上,△是以点M为直角顶点的等腰直角三角形.(1)求证点M为边BC的中点;(2)求点C到平面的距离;(3)求二面角的大小.21.(本题12分)已知三棱锥中,,,⊥平面,,分别是上的动点,且,(Ⅰ)求证:不论为何值,总有平面⊥平面;(Ⅱ)当为何值时,平面⊥平面?用心爱心专心22.(本题14分)空间折线ABCD中,AB、BC、CD两两垂直.(1)在以A、B、C、D为顶点的三棱锥中,写出以棱锥的各棱为棱,为棱锥的各面为面的二面角中所有的直二面角;(2)若AD与平面BCD所成角为α,AD与平面ABC所成角为β,求α+β的范围及二面B-AD-C的平面角的余弦;(3)若AD为定值,问α、β为何值...