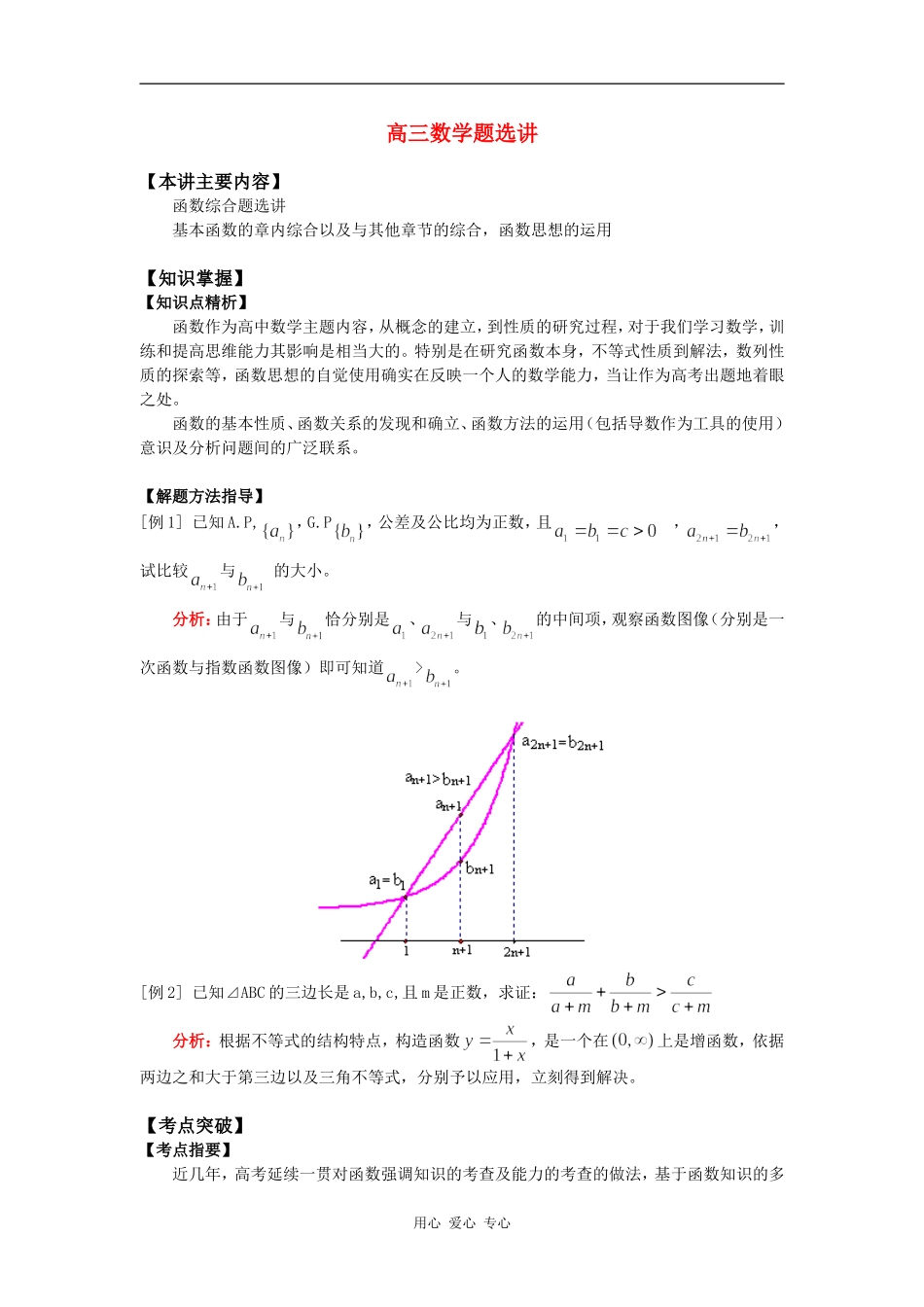
高三数学题选讲【本讲主要内容】函数综合题选讲基本函数的章内综合以及与其他章节的综合,函数思想的运用【知识掌握】【知识点精析】函数作为高中数学主题内容,从概念的建立,到性质的研究过程,对于我们学习数学,训练和提高思维能力其影响是相当大的。特别是在研究函数本身,不等式性质到解法,数列性质的探索等,函数思想的自觉使用确实在反映一个人的数学能力,当让作为高考出题地着眼之处。函数的基本性质、函数关系的发现和确立、函数方法的运用(包括导数作为工具的使用)意识及分析问题间的广泛联系。【解题方法指导】[例1]已知A.P,,G.P,公差及公比均为正数,且,,试比较与的大小。分析:由于与恰分别是、与、的中间项,观察函数图像(分别是一次函数与指数函数图像)即可知道>。[例2]已知⊿ABC的三边长是a,b,c,且m是正数,求证:分析:根据不等式的结构特点,构造函数,是一个在上是增函数,依据两边之和大于第三边以及三角不等式,分别予以应用,立刻得到解决。【考点突破】【考点指要】近几年,高考延续一贯对函数强调知识的考查及能力的考查的做法,基于函数知识的多用心爱心专心元连续性,综合性较高,与其它知识的联系形式存在于有形与无形之间。【典型例题分析】[例1](06上海)若曲线与直线没有公共点,则的取值范围是略解:画出函数的图像即可解决,结果为-10)C.f(2x)=2e2x(xD.f(2x)=lnx+ln2(x>0)用心爱心专心2.过点(-1,0)作抛物线的切线,则其中一条切线为()3.对,记函数的最小值是()A.0B.C.D.34.(06湖北)关于x的方程(x2-1)2-|x2-1|+k=0,给出下列四个命题:①存在实数k,使得方程恰有2个不同的实根②存在实数k,使得方程恰有4个不同的实根③存在实数k,使得方程恰有5个不同的实根④存在实数k,使得方程恰有8个不同的实根其中假命题的个数是()A.0B.1C.2D.35.(05辽宁)已知是定义在R上的单调函数,实数,,,。若,则()A.B.C.D.6.(05辽宁)一...