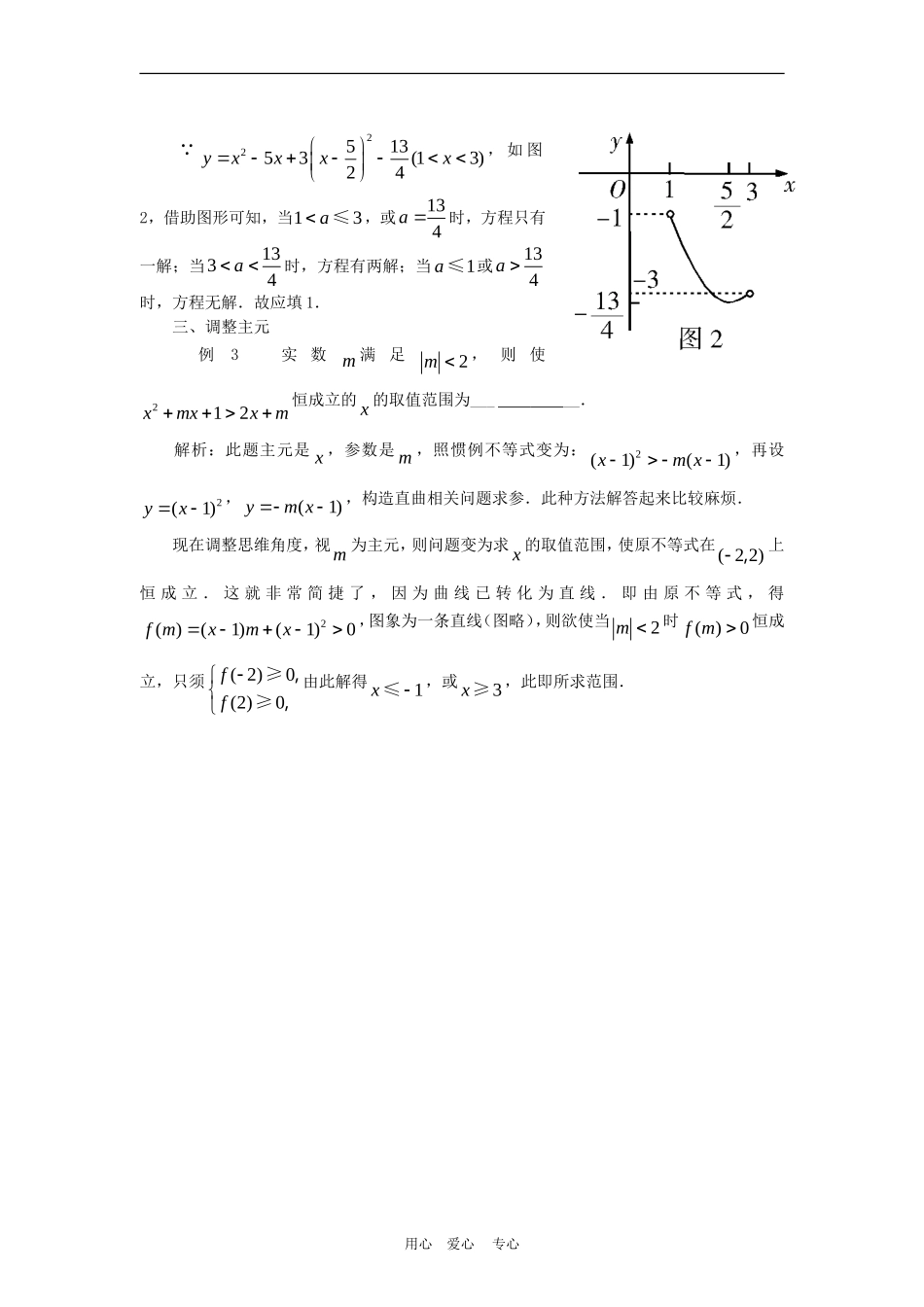
避繁就简话构图――谈数形结合的图形调控数形结合作为重要的数学思想,有着广泛的应用,但在具体运用时要善于进行理性思考即进行思维调整,以发挥出最好的功效.数形结合离不开构图,那么构图有哪些讲究呢?下面我们结合几个例子说明.一、调整关系例1对任意角,2sin2cos410mm恒成立,则m的取值范围是_____.解析:对此题通常是变sin为cos,整理成降幂排列式:2cos2cos40mm,于是一个二次不等式便显露出来了,便可建构曲线:令cosx,则222()24()(4)([11])fxxmxmxmmmx,,这就需要分对称轴xm在区间[11],的左侧、内部、右侧三种情况构图求解.因为需要讨论三种情况,显然较繁.现在我们做如下调控:既然问题是求m的取值范围,使不等式2240xmxm在[11],上恒成立,于是可将不等式变为22(2)xmx,这样可建构直曲相关的图形求解,比前一种方法简捷多了.设2yx,[11]x,,2(2)ymx,则后者为过定点(20),的直线.如图1,欲使22(2)xmx在[11],上恒成立,只须20m,即0m便可.二、调整直线例2当13a≤时,关于x的方程lg(1)lg(3)lg()xxax根的个数为_____.解析:原方程为2lg(43)lg()xxax,即243(13)xxaxx,若直接构图,问题即为讨论直线yxa与抛物线(弧)243yxx的关系.因为直线是倾斜的,当其与抛物线相切时得用判别式求a的值.接下来还得按a分类,确定方程根的个数.这种数形结合方式的运算,主要是在求当直线与曲线相切时a的值,须化成一元二次方程,用判别式解决,不算太简捷.如若调整思维,联想到方程243(13)xxaxx等价于253(13)xxax,于是有另一种构图方式.其简捷之处在于直线不是倾斜的而是平行于x轴.用心爱心专心∵2251353(13)24yxxxx,如图2,借助图形可知,当13a≤,或134a时,方程只有一解;当1334a时,方程有两解;当a≤或134a时,方程无解.故应填1.三、调整主元例3实数m满足2m,则使212xmxxm恒成立的x的取值范围为_____.解析:此题主元是x,参数是m,照惯例不等式变为:2(1)(1)xmx,再设2(1)yx,(1)ymx,构造直曲相关问题求参.此种方法解答起来比较麻烦.现在调整思维角度,视m为主元,则问题变为求x的取值范围,使原不等式在(22),上恒成立.这就非常简捷了,因为曲线已转化为直线.即由原不等式,得2()(1)(1)0fmxmx,图象为一条直线(图略),则欲使当2m时()0fm恒成立,只须(2)0(2)0ff,,≥≥由此解得1x≤,或3x≥,此即所求范围.用心爱心专心