高三数学解题方法谈：数形结合巧求最值VIP免费

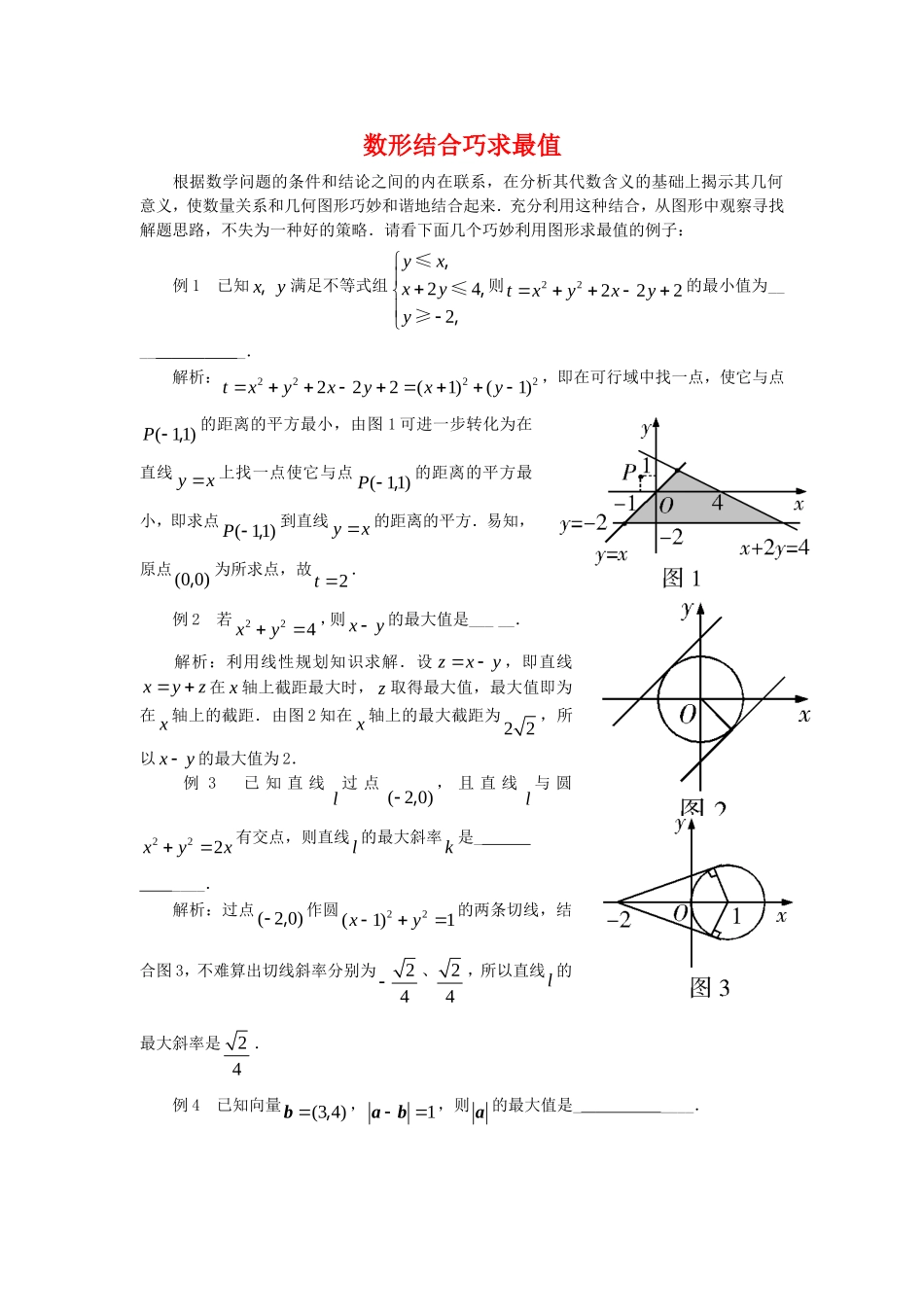
数形结合巧求最值根据数学问题的条件和结论之间的内在联系，在分析其代数含义的基础上揭示其几何意义，使数量关系和几何图形巧妙和谐地结合起来．充分利用这种结合，从图形中观察寻找解题思路，不失为一种好的策略．请看下面几个巧妙利用图形求最值的例子：例1已知xy，满足不等式组242yxxyy，，，≤≤≥则22222txyxy的最小值为_____．解析：2222222(1)(1)txyxyxy，即在可行域中找一点，使它与点(11)P，的距离的平方最小，由图1可进一步转化为在直线yx上找一点使它与点(11)P，的距离的平方最小，即求点(11)P，到直线yx的距离的平方．易知，原点(00)，为所求点，故2t．例2若224xy，则xy的最大值是_____．解析：利用线性规划知识求解．设zxy，即直线xyz在x轴上截距最大时，z取得最大值，最大值即为在x轴上的截距．由图2知在x轴上的最大截距为22，所以xy的最大值为2．例3已知直线l过点(20)，，且直线l与圆222xyx有交点，则直线l的最大斜率k是_____．解析：过点(20)，作圆22(1)1xy的两条切线，结合图3，不难算出切线斜率分别为24、24，所以直线l的最大斜率是24．例4已知向量(34)，b，1ab，则a的最大值是_____．解析：如图4，设34OB�，b=，OA�a，由向量减法及模的几何意义可知，点A在以B为圆心，1为半径的圆上．由图可知，当点A在A位置时取得最大值，此时max6a．例5（2004年湖南·文科）已知向量cossin，a=，31，b=，则2ab的最大值、最小值分别是（）．（Ａ）420，（Ｂ）442，（Ｃ）170，（Ｄ）40，解析：由已知得22cos2sin，a=，向量2a所表示的点为圆224xy上的动点，2ab表示点(31)，到圆上点的距离．因为向量31，b=表示的点也在圆224xy上（如图5），由图易知，2ab的最大值为4，最小值为0，故选（D）．例6在ABC△中，O为中线AM上一个动点，若2AM，则()OAOBOC�的最小值是_____．解析：构造图形．如图6，以线段OB、OC为邻边构造OBDC，则点M是其对角线的交点，有2OBOCOM�，又向量OM�，OA�反向，故()2OAOBOCOAOM�．而2OAOMAM�，由均值不等式，有222OAOMOAOM��≥，当且仅当1OAOM�，即O为AM的中点时取等号．故所求最小值是2．