高三数学理导数（三）人教实验版（A）知识精讲VIP免费

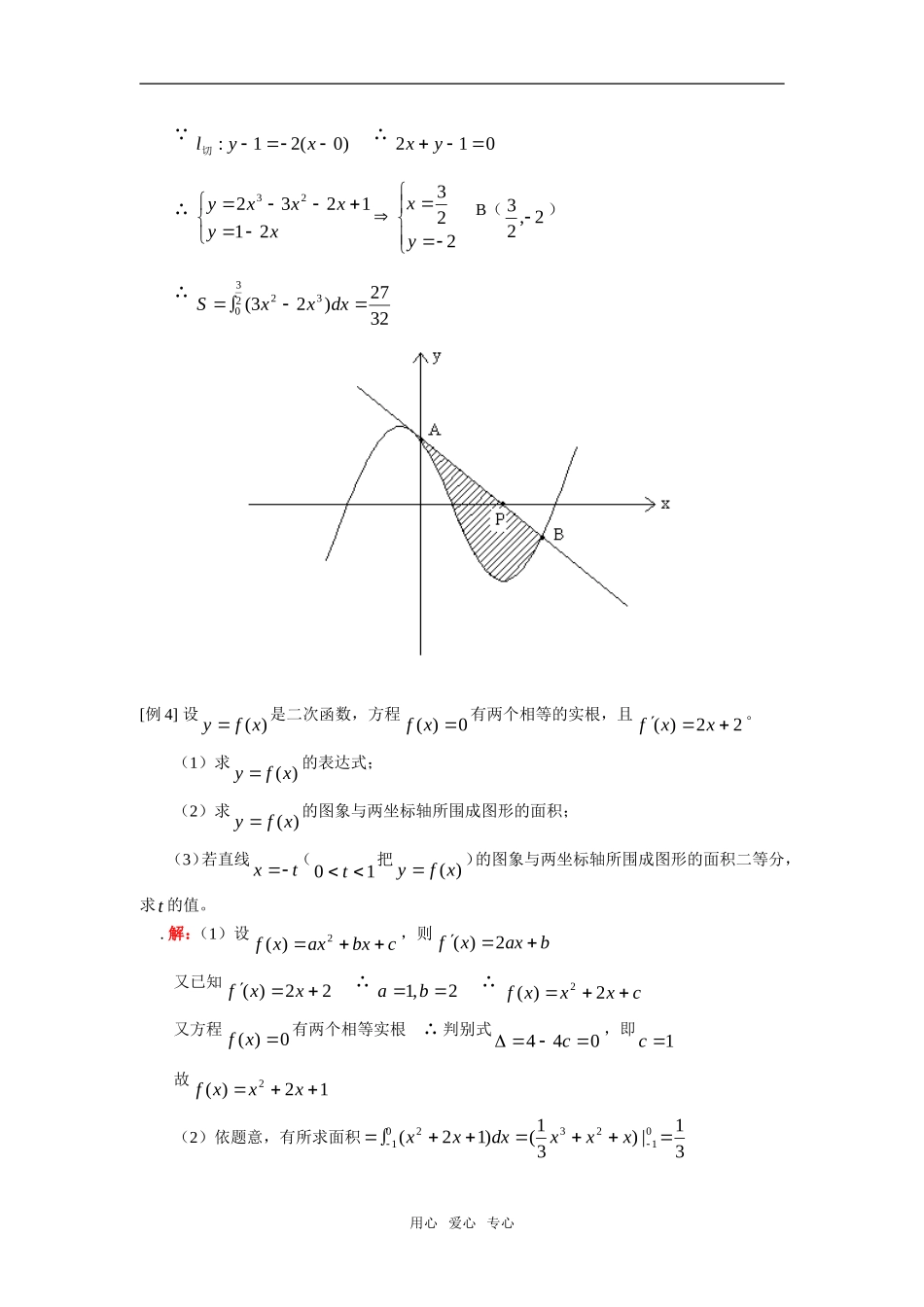
高三数学理导数（三）人教实验版（A）【本讲教育信息】一.教学内容：导数（三）（理）二.重点、难点：1.基本积分表（1）cdx0（2）cxdx1（3）cxndxxnn111（4）cxdxxln1（5）cxxdxcossin（6）cxxdxsincos（7）cedxexx（8）caadxaxxln2.运算公式（1）dxxfkdxxfkbaba)()(（2）dxxgdxxfdxxgxfbababa)()()]()([（3）bacabcbcadxxfdxxfdxxf)()()()(其中3.)()(|)()(aFbFxFdxxfbabaninbafnabdxxf1)(lim)(【典型例题】[例1]求下列定积分（1）dxxx)cossin2(20xdxxdxcossin22020用心爱心专心3)01()10(2|sin|cos22020x（2）dxx)1(220 1012111222xxxxxy∴dxxdxxdxx)1()1(12212102202)131()238()311(|)3(|)3(213103xxxx[例2]dxbaxxM2311)(，ba,为何值时，M最小。解：dxbaxxbaxxM])(2)[(23231117582)53(32)315271(2|)315271(2)2(2222210232572224610babaaxbxaaxxdxbxaaxx∴0,53ba时，1758minM[例3]曲线C：123223xxxy，点)0,21(P，求过P的切线l与C围成的图形的面积。解：设切点),(000yxP，则266020xxy切线l：))(266(]1232[002002030xxxxxxxy过P（0,21）∴]21[]266[]1232[002002030xxxxxx0)364(0200xxx∴1,000yxA（0，1）用心爱心专心 )0(21:xyl切∴012yx∴22321123223yxxyxxxyB（2,23）∴3227)23(32230dxxxS[例4]设)(xfy是二次函数，方程0)(xf有两个相等的实根，且22)(xxf。（1）求)(xfy的表达式；（2）求)(xfy的图象与两坐标轴所围成图形的面积；（3）若直线tx（10t把)(xfy）的图象与两坐标轴所围成图形的面积二等分，求t的值。.解：（1）设cbxaxxf2)(，则baxxf2)(又已知22)(xxf∴2,1ba∴cxxxf2)(2又方程0)(xf有两个相等实根∴判别式044c，即1c故12)(2xxxf（2）依题意，有所求面积31|)31()12(0123201xxxdxxx用心爱心专心（3）依题意，有dxxxdxxxtt)12()12(2021∴023123|)31(|)31(ttxxxxxxtttttt2323313131，0166223ttt∴1)1(23t，于是3211t[例5]已知.ln2)(),()(2xxgRaaxxf（1）讨论函数)()()(xgxfxF的单调性；（2）是否存在这样的a的值，使得)(2)()(*Rxxgxf恒成立，若不存在，请说明理由；若存在，求出所有这样的值。（1）),0(,ln2)(2其定义域为xaxxF)0()1(222)(2xxaxxaxxF（i）当axaxaxaxa1001.101,022得由得由时故当).1,0(),,1()(,0aaxFa递减区间为的递增区间为时（ii）当)0(0)(,0xxFa时恒成立故当),0()(,0在时xFa上单调递减（2）即使02)(xxF在时恒成立.由（1）可知当.)(,,0xFxa则时02)(xxF在时不可能恒成立0a，由（1）可知aaaFxF1ln11ln21)1()(min21ln1a只须即可eaa1ln用心爱心专心故存在这样的a的值，使得.)(2)()(恒成立Rxxgxf.,ea的取值范围为[例6]已知函数32()fxaxbxcx在点0x处取得极小值－4，使其导数'()0fx的x的取值范围为(1,3)，求：（1）()fx的解析式；（2）若过点(1,)Pm可作曲线()yfx的三条切线，求实数m的取值范围。（1）由题意得：2'()323(1)(3),(0)fxaxbxcaxxa∴在(,1)上'()0fx；在(1,3)上'()0fx；在(3,)上'()0fx在此()fx在01x处取得极小值4∴4abc①'(1)320fabc②'(3)2760fabc③由①②③联立得：169abc∴32()69fxxxx（2）设切点Q(,())tft,()()()yftftxt232(3129)()(69)yttxtttt222(3129)(3129)...