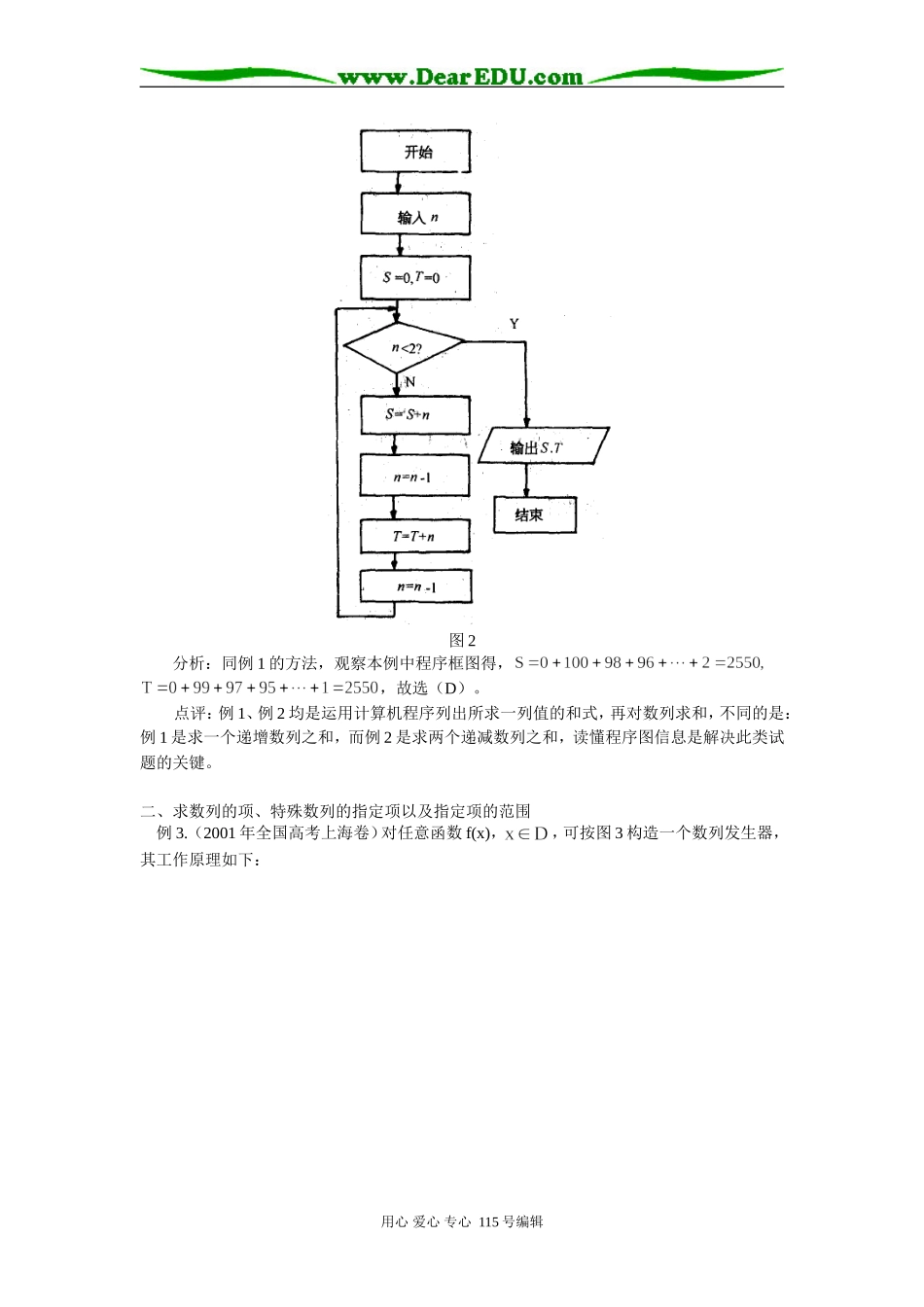
数列在计算机技术中的应用毛传宝随着计算机技术的普及,近年来许多省市的高考试卷中,围绕数列知识,出现了一大批以“计算机技术”为背景,既考查知识又注重能力的创新题,归纳起来主要有:一、数列求和例1.(2007年全国高考海南省、宁夏卷)如果执行图1的程序框图,那么输出的S等于()A.2450B.2500C.2550D.2652分析:观察程序框图得当时,;当时,;当时,;…;当时,;当时则输出S值,故输出的,选(C)。例2.(2007年全国高考山东卷)阅读如图2程序框图,若输出的n是100,则输出的变量S和T的值依次是()A.2500,2500B.2550,2550C.2500,2550D.2550,2500用心爱心专心115号编辑图2分析:同例1的方法,观察本例中程序框图得,,故选(D)。点评:例1、例2均是运用计算机程序列出所求一列值的和式,再对数列求和,不同的是:例1是求一个递增数列之和,而例2是求两个递减数列之和,读懂程序图信息是解决此类试题的关键。二、求数列的项、特殊数列的指定项以及指定项的范围例3.(2001年全国高考上海卷)对任意函数f(x),,可按图3构造一个数列发生器,其工作原理如下:用心爱心专心115号编辑(1)输入数据,经过数列发生器输出;(2)若,则数列发生器结束工作;若,则将反馈回输入端,再输出,并依此规律继续下去。现定义(1)若输入,则由数列发生器产生数列,请写出数列的所有项;(2)若要数列发生器产生一个无穷的常数数列,试求输入的初始数据的值;(3)若输入时,产生的无穷数列满足:对任意正整数n,均有,求的取值范围。分析:(1)由得,f(x)定义域。当时,即数列发生器结束工作,故数列只有三项,即;(2)因数列发生器产生的数列为无穷的常数列,由=x,即,解得x=1或,即当或2时,,故当时,;当时,,即满足题设的值或2;(3)由题意,数列发生器产生的数列为无穷递增数列。解不等式,得或,要使,则或。由于,当时,;当时,,且,依次类推,可得数列的所有项均满足,综上所述,,再由,再由,得。点评:本例是运用“新技术”分别求一般数列、常数列和无穷递增数列在特定条件()下的项、指定项及指定项的范围。可见计算机应用于数学,能产生意想不到的效果。用心爱心专心115号编辑三、求数列通项例4.(2004年全国高考上海卷)如图4是一个计算机装置示意图,是数据入口处,C是计算机结果的出口,计算(过程是由分别输入自然数m和n,经过计算后得自然数由C输出,此种计算机装置完成的计算满足以下三个性质:(1)若分别输入1,则输出结果为1;(2)若输入任何固定自然数不变,输入自然数增大1,则输出结果比原来增大2;(3)若输入1,输入自然数增大1,则输出的结果为原来的2倍。试问:(1)若输入1,输入自然数n,输出结果为多少?(2)若输入1,输入自然数m,输出结果为多少?分析:本题可考虑设二元函数式,设,则由题意。于是:(1)在中,令,则,由此可知:组成以f(1,1)为首项,2为公差的等差数列,故即输出结果为。(2)因为,所以组成以为首项,2为公比的等比数列,故。即输出结果为。点评:本例的信息语言粗看不知如何下手,若细品装置的作用,发现可把条件写成二元函数式,将信息语言符号化,从而抽象出等差数列和等比数列的模型,使问题迅速获解。四、根据数列的某几项和确定计算机在流程框内的条件例5.(2007年全国高考广东卷)图5是某县参加2007年高考的学生身高条形统计图,从左到右的各条形表示的学生人数依次记为[如表示身高(单位:cm)在内的学生人数]。图6是统计图5中身高在一定范围内学生人数的一个算法流程图。现要统计身高在160~180cm(含160cm,不含180cm)的学生人数,那么在流程图中的判断框内应填写的条件是()。A.B.C.D.用心爱心专心115号编辑分析:由图5知,身高在160~180cm之间的人数为,即数列的第4项至第7项之和为。再由图6知,当算法流程图中的判断框时,,即。故选(C)。点评:本题将文字、统计图和计算机三种语言结合在一起,乍一看很难,如果细心阅读,将它们转化为数学符号语言,则可迅速求解。用心爱心专心115号编辑