高中数学总复习高中数学总复习对数和指数函数复习内容:高中数学第三章【复习目标】1.理解对数的意义,会熟练的将指数式与对数式互化,掌握积、商、幂的对数运算性质换底公式;2.理解反函数的概念,会求已知函数的反函数,掌握函数与它的反函数在定义域、值域及图像上的关系;3.理解指数函数和对数函数的要领,掌握指数函数和对数函数的图像和性质,掌握指数函数和对数函数互为反函数的结论;4.理解指数方程和对数方程的意义,会解简单的指数方程和对数方程.5.掌握数学方法:分类讨论,数形结合,换元法,等价转换.【重点难点】对数的意义与运算性质,反函数的概念及性质,指数函数和对数函数的图像和性质.【课前预习】1.函数、、、中,指数函数是2.(1)函数的值域是(2)函数的值域是3.(1)函数的定义域是;值域是(2)函数的定义域是;值域是4.(1)函数的图像与函数的图像关于x轴对称,则=(2)函数的图像关于x轴对称的函数=5.函数是R上的减函数,则实数a的取值范围是6.已知0
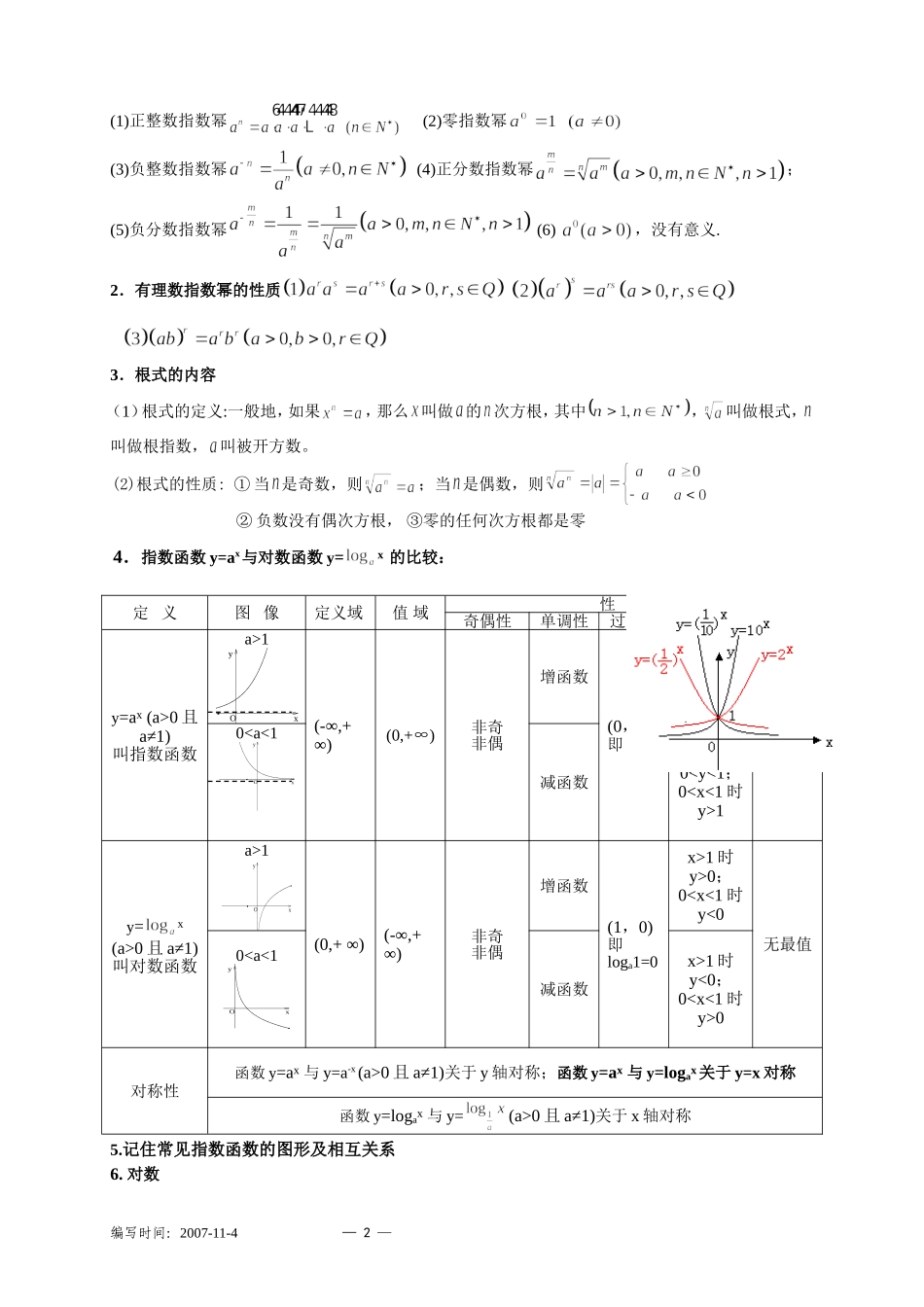
0且a≠1)叫指数函数a>1Oyx(-∞,+∞)(0,+∞)非奇非偶增函数(0,1)即a0=1x>0时y>1;00时01y=x(a>0且a≠1)叫对数函数a>1Oyx(0,+∞)(-∞,+∞)非奇非偶增函数(1,0)即loga1=0x>1时y>0;01时y<0;00对称性函数y=ax与y=a-x(a>0且a≠1)关于y轴对称;函数y=ax与y=logax关于y=x对称函数y=logax与y=(a>0且a≠1)关于x轴对称(1)对数的概念如果,那么b叫做以a为底N的对数,记(2)对数的性质:①零与负数没有对数;②;③(3)对数的运算性质;其中a>0,a≠0,M>0,N>0;(4)对数换底公式:7.记住常见对数函数的图形及相互关系8.几个注意点(1)函数y=ax与对数函数y=logax(a>0,a≠1)互为反函数,从概念、图象、性质去理解它们的区别和联系;(2)研究对数函数问题,尽量化为同底,并注意对数问题中的定义域限制【例题分析】1.指对数互化1.,则a=;2.3x=16,则x=;3.,则x=;2.换底公式及应用1.,2.用表示=3.定义域、值域问题【例1】(1)写出下列函数的定义域和值域:(1);(2);(3)R;(0,+∞);(-∞,0)∪(0,+∞);[0,+∞];[1,+∞](2)已知函数f(x)=loga(1-ax)(a>0且a≠1)①求f(x)的定义域、值域;②证明:f(x)在定义域上是减函数.【例2】(1)函数的定义域是(1)函数的定义域是(2)函数的值域是(4)若函数的定义域和值域都是[0,1]则等于()A.B.C.D.24.单调性、奇偶性问题编写时间:2007-11-4—3—【例3】(1)求函数的单调区间;(3)比较三数的大小:2x;(0.2)x;(x>0);(2x>>(0.2)x)(4)函数在区间(0,+∞)上是()A.增函数且y>0B.增函数且y<0C.减函数且y>0D.减函数且y<0(5)已知①讨论y的单调性;②求y的最值,并求取的最值时的x的值;③作出函数的大致图像。(6)函数,x∈[0,1]的最小值为(7)函数(a>0且a≠1),在区间[1,2]上的最大值比最小值大,则a的值为或(8)若函数在区间上的最大值是最小值的3倍,则等于(A)A.B.C.D.(9)是函数为偶函数的...