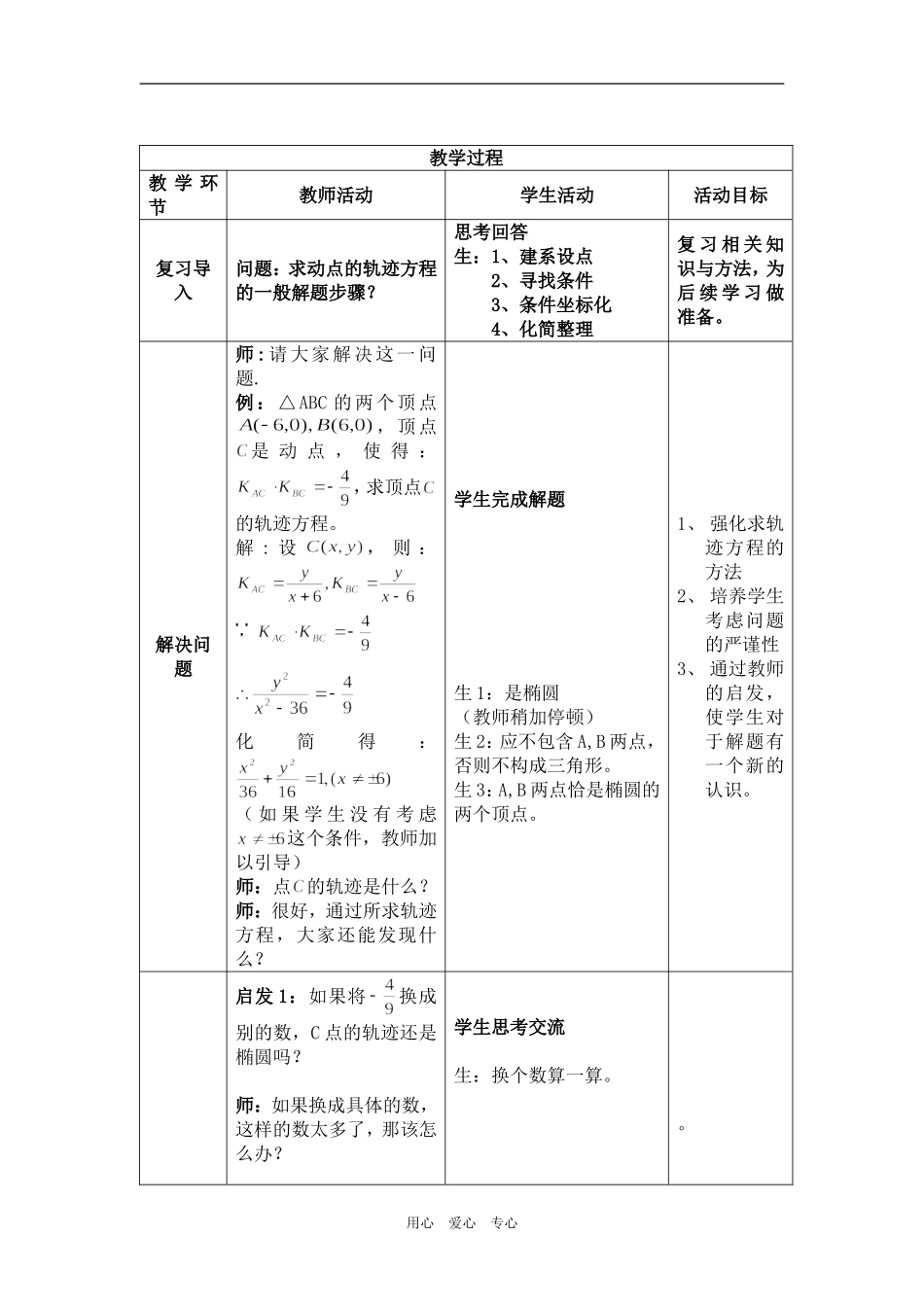
数学北京市八大处中学韩维祥高二(1)班圆锥曲线方程的应用设计思想以建构主义理论为指导,对圆锥曲线方程的应用进行教学设计。设计以学生为中心,以认识科学的研究方法和发展学生的思维为目标,展示学生发现、研究问题的过程,强调教师对教学的组织和引导,突出学生主动学习的过程和再创造的活动。以波利亚的问题解决模式为思维主线,在问题解决过程中,让学生在掌握知识、形成技能的同时,培养能力,发展智力。依据中学数学新课程标准,课堂教学中,注重对学生激励评价,建立平等、民主的师生关系,以促进学生全面、和谐的发展。现代信息技术作为学生学习数学和解决问题的强有力工具,致力于改变学生的学习方式,使学生乐意并有更多的精力投入到现实的,探索性的数学活动中去.故本节课采用探究式和讨论式相结合的学习方式,运用现代信息技术,调动学生学习的积极性,充分体现学生的主体地位。学生学习分析学生特征学生的数学基础比较薄弱,学习数学的主动性和创造性不够。学生在此之前已经学完了椭圆和双曲线的有关知识,对于解析几何所解决的两大问题,有了一定的认识。但是学生自主发现问题、研究问题的意识不强,通过本节课的研究,希望学生对这一问题有所领悟。学习方式本节课采用自主探究式和合作式相结合的学习方式教师教学分析教材分析解析几何研究的两大问题是:求曲线方程和通过方程研究曲线的性质,这是解析几何的知识主线。本节教学内容是对于一道教材习题的进一步研究,这是很有必要的。这不仅符合考纲的要求:充分发挥教材的作用,更是对学生数学素养的培养和提高具有积极的推动作用。教学目标1、知识目标:会求动点的轨迹方程;会通过方程研究曲线的性质。2、能力目标:通过对问题的不断深入的探究,渗透数形结合的数学思想,培养学生对问题的观察、分析、归纳和概括能力。引导学生学习研究问题的一般方法及联想、类比、猜测等合情推理与逻辑推理方法,培养学生思维的深刻性、创造性、科学性与批判性,提高学生分析综合能力及探索发现能力.3、情感目标:通过营造民主、开放的课堂教学氛围,培养学生敢想、敢说、坚韧不拔的意志及勇于探索、发现、创新的精神等个性品质.教学重点圆锥曲线方程的应用教学难点对问题的深入研究的一般方法的培养用心爱心专心教学方法引导发现式、讨论交流式。教学流程复习引入练习强化提出探究问题课件演示讨论、研究否判断能否解决引导帮助能归纳总结成果应用学生小结布置作业用心爱心专心教学过程教学环节教师活动学生活动活动目标复习导入问题:求动点的轨迹方程的一般解题步骤?思考回答生:1、建系设点2、寻找条件3、条件坐标化4、化简整理复习相关知识与方法,为后续学习做准备。解决问题师:请大家解决这一问题.例:△ABC的两个顶点,顶点是动点,使得:,求顶点的轨迹方程。解:设,则:化简得:(如果学生没有考虑这个条件,教师加以引导)师:点的轨迹是什么?师:很好,通过所求轨迹方程,大家还能发现什么?学生完成解题生1:是椭圆(教师稍加停顿)生2:应不包含A,B两点,否则不构成三角形。生3:A,B两点恰是椭圆的两个顶点。1、强化求轨迹方程的方法2、培养学生考虑问题的严谨性3、通过教师的启发,使学生对于解题有一个新的认识。启发1:如果将换成别的数,C点的轨迹还是椭圆吗?师:如果换成具体的数,这样的数太多了,那该怎么办?学生思考交流生:换个数算一算。。用心爱心专心深入探究(课件演示)师:这是一个很值得我们思考的问题,那么怎样研究这个问题?师:很好!这就是研究问题、解决问题的方法:由特殊到一般。我们不妨将问题一般化。探究1:△ABC的两个顶点,顶点是动点,使得:,求顶点的轨迹方程。解:设,则:化简得:师:C点的轨迹方程一定是椭圆的方程吗?适当点拨、课件演示、整理归纳、投影显示、师:通过将问题进行一般化的研究,我们对椭圆和双曲线又有了一个全新的认识,你能叙述一下吗?学生观察思考生:那就换成一个字母表示所有的数。学生解答问题学生自主研究、讨论交流、陈述观点、达成共识、归纳总结。1、通过问题的提出,引发学生的思考,调动学生的积极性;2、课件的演示,使学生对于问题的...