高三数学上学期第一次质量检查试题 文-人教版高三全册数学试题VIP免费

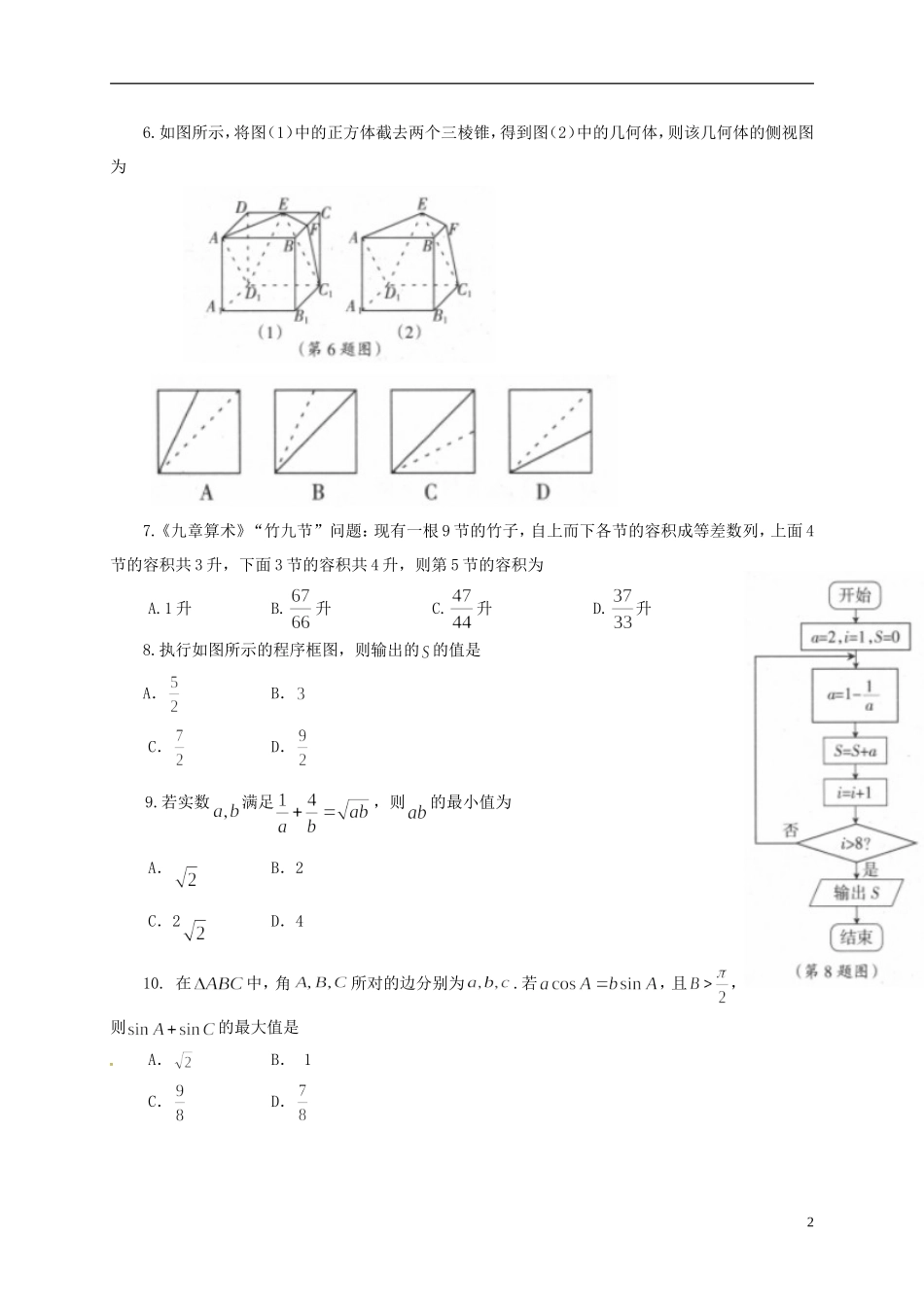
福州八中2016—2017学年高三毕业班第一次质量检查数学(文)试题一、选择题：本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1.设，则A．B．C．D．2.设平面向量，若，则等于（）A．4B．5C．D．3.将函数sin(2)3yx图象上的点(,)4Pt向左平移s（0s）个单位长度得到点'P，若'P位于函数sin2yx的图象上，则A.12t，s的最小值为6B.32t，s的最小值为6C.12t，s的最小值为3D.32t，s的最小值为34.下列说法正确的是A．若“pq”为假命题，则p，q均为假命题B．“2x”是“2320xx”的必要不充分条件C．命题“xR，使得210xx”的否定是：“xR，均有210xx”D．在ABC中若A是最大角，则“222sinsinsinBCA”是“ABC为钝角三角形”的充要条件5.若实数满足若的最小值是A．B．C．D．16.如图所示，将图（1）中的正方体截去两个三棱锥，得到图（2）中的几何体，则该几何体的侧视图为7.《九章算术》“竹九节”问题：现有一根9节的竹子，自上而下各节的容积成等差数列，上面4节的容积共3升，下面3节的容积共4升，则第5节的容积为A.1升B.升C.升D.升8.执行如图所示的程序框图，则输出的的值是A．B．C．D．9.若实数满足，则的最小值为A．B．2C．2D．410.在中，角所对的边分别为.若，且，则的最大值是A．B．1C．D．2xyO22（第17题）3311.已知，若圆与双曲线有公共点，则该双曲线离心率的取值范围是A．B．C．D．12.已知可导函数的导数满足,则A.B.C.D.的大小不确定第Ⅱ卷（共90分）二、填空题（每题5分，满分20分，将答案填在答题纸上）13.已知复数满足，则．14.若为内一点，且，在内随机撒一颗豆子，则此豆子落在内的概率为为．15.若函数在其定义域内的一个子区间内不是单调函数，则实数k的取值范围．16.若函数有零点，则实数的取值范围是．三、解答题：本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.17.（本小题满分12分）已知函数()sin()fxAx（其中A，，为常数，且A＞0，＞0，22＜＜）的部分图象如图所示．（1）求函数f(x)的解析式；（2）若，求sin(2)6的值．18.（本小题满分12分）在中，角，，的对边分别为，，，已知向量，，且．（1）求角的大小；（2）若，求面积的最大值．319.（本小题满分12分）已知R，函数=.（1）当时，解不等式>1；（2）若关于的方程+=0的解集中恰有一个元素，求的值；（3）设>0，若对任意，函数在区间上的最大值与最小值的差不超过1，求的取值范围.20.（本小题满分12分）如图，，，三地有直道相通，千米，千米，千米.现甲、乙两警员同时从地出发匀速前往地，经过小时，他们之间的距离为（单位：千米）.甲的路线是，速度为千米/小时，乙的路线是，速度为千米/小时.乙到达地后原地等待.设时乙到达地.（1）求与的值；（2）已知警员的对讲机的有效通话距离是千米.当时，求的表达式，并判断在上得最大值是否超过千米？说明理由.21、（本小题满分12分）已知函数（1）若函数在上单调递减，求实数的取值范围；（2）当时，有两个零点，且，求证：。请考生在22、23、24三题中任选一题作答，如果多做，则按所做的第一题记分.22.（本小题满分10分）选修4-1：几何证明选讲如图，是⊙的切线，是⊙的割线，，连接，分别于⊙交于点，4点.（Ⅰ）求证：；（Ⅱ）求证：.23.（本小题满分10分）选修4-4：坐标系与参数方程在直角坐标系xoy中，直线l的参数方程为：ktytx1（t为参数），以O为原点，ox轴为极轴，单位长度不变，建立极坐标系，曲线C的极坐标方程为：cos4sin2（Ⅰ）写出直线l和曲线C的普通方程。（Ⅱ）若直线l和曲线C相切，求实数k的值。24.（本小题满分10分）选修4-5：不等式选讲已知关于x的不等式|x+1|+|x-2|≤(a+b1)(ba1)对任意正实数a、b恒成立，求实数x的取值范围。5福州八中2016—2017学年高三毕业班第一次质量检查数学(文)试卷参考答案及评分标准一、选择题（每小题5分,共60分）1.C2.D3.A4.D5.B6.B7.B8.A9.D10.C11.D12.A二、填空题（每题5分，满分20分）13.3-4i14.15.16.三、解答题：本大题共6小题，共70...