高三数学上学期周周清同步检测试题-人教版高三全册数学试题VIP免费

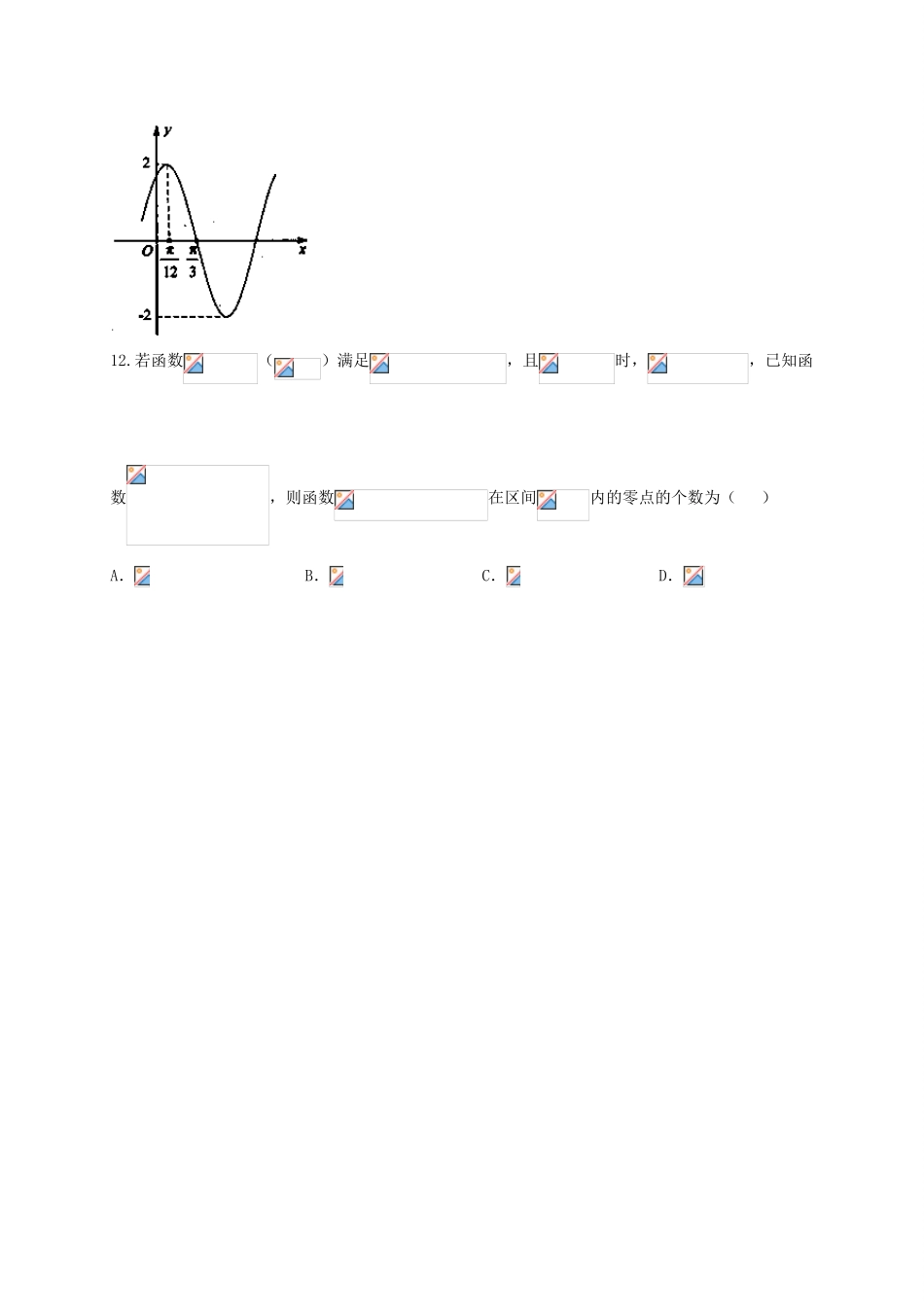
山东省滕州市高考补习学校2016-2017学年第一学期周周清同步检测数学试题第I卷（选择题）一、选择题1.设集合，集合，则（）A．B．（﹣∞，1]C．D．2.已知向量=（cosθ，sinθ），向量=（），且，则tanθ的值是（）A．B．C．D．3.若函数是定义在上的偶函数，则该函数的最大值为A．5B．4C．3D．24.设变量x，y满足约束条件，则目标函数z=3x﹣y的取值范围是（）A．B．C．[﹣1，6]D．5.数列{an}，满足对任意的n∈N+，均有an+an+1+an+2为定值．若a7=2，a9=3，a98=4，则数列{an}的前100项的和S100=（）A．132B．299C．68D．996.已知是两条不同的直线，是两个不同的平面，下列命题为真命题的序号是（）①若，则；②若，则；③若,则；④若，则．A．①④B．①③C．②④D．②③7..下列函数中，既是偶函数又存在零点的是（）A．y=lnxB．y=x2+1C．y=sinxD．y=cosx8.如图所示为某几何体的正视图和侧视图，则该几何体体积的所有可能取值的集合是A．B．C．D．9.若向量，，则以下向量中与垂直的是（）A．B．C．D．10.已知向量=（1，﹣2），=（3，m），若∥（2+），则实数m的值为（）A．﹣6B．C．6D．11.已知函数（，，）的部分图象如图所示，则（）A．B．C．D．2侧视图11正视图12.若函数（）满足，且时，，已知函数，则函数在区间内的零点的个数为（）A．B．C．D．第II卷（非选择题）二、填空题13.在半径为5的球面上有不同的四点A、B、C、D，若，则平面BCD被球所截面图形的面积为.14.设空间向量，，且，则，．15.设等差数列的前项和为，已知，，则．16.已知实数，满足，若目标函数的最大值为，最小值为，则实数的取值范围是．17.已知，，则．三、解答题18.（本小题满分12分）设数列的前n项和为，满足，且.（Ⅰ）求的通项公式；（Ⅱ）若成等差数列，求证：成等差数列.19.（本题满分14分）本题共有2小题，第(1)小题满分6分，第(2)小题满分8分．如图，在长方体中，，，点在棱上移动．（1）证明：；（2）等于何值时，二面角的大小为．20.(本小题满分12分)如图，矩形所在的平面与等边所在的平面垂直，，为的中点．（1）求证：；（2）求二面角的余弦值.21.（1）已知0<α<β<，sinα=,cos(α−β)=，求cosβ的值；（2）在ΔABC中，sinA−cosA=，求cos2A的值。22.(本小题满分12分)已知数列满足：,，，().（1）求证：是等差数列，并求出；D1D1C1C1A1A1AAEEDDB1B1BBCCOOxxyyzz（2）证明：.23.（本小题满分12分）已知函数，．求的值；若，，求的值．试卷答案1.A试题分析：由，解得，，则.考点：1.函数的定义域；2.函数的值域；3.交际的定义；2.C【考点】平面向量数量积的运算；数量积判断两个平面向量的垂直关系．【分析】由题意可得=0，即cosθ+sinθ=0，化简得tanθ的值．【解答】解：由于已知向量=（cosθ，sinθ），向量=（），且，则=0，即cosθ+sinθ=0，化简得tanθ=﹣，故选C．3.A4.A【考点】简单线性规划．【分析】作出不等式组表示的平面区域；作出目标函数对应的直线；由目标函数中z的几何意义可求z的最大值与最小值，进而可求z的范围【解答】解：作出不等式组表示的平面区域，如图所示由z=3x﹣y可得y=3x﹣z，则﹣z为直线y=3x﹣z在y轴上的截距，截距越大，z越小结合图形可知，当直线y=3x﹣z平移到B时，z最小，平移到C时z最大由可得B（，3），由可得C（2，0），zmax=6∴故选A5.B【考点】数列的求和．【分析】对任意的n∈N+，均有an+an+1+an+2为定值，可得（an+1+an+2+an+3）﹣（an+an+1+an+2）=0，an+3=an，于是{an}是以3为周期的数列，即可得出．【解答】解：对任意的n∈N+，均有an+an+1+an+2为定值，∴（an+1+an+2+an+3）﹣（an+an+1+an+2）=0，故an+3=an，∴{an}是以3为周期的数列，故a1=a7=2，a2=a98=4，a3=a9=3，∴S100=（a1+a2+a3）+…+（a97+a98+a99）+a100=33（2+4+3）+a1=299．故选：B．6.试题分析：由无法推出，只有当是相交直线时，才能得到，①不正确；由直线与平面平行的性质可知，若，那么，②正确；若,可能有或，③不正确；由可知，，又，所以，，④正确.故选.考点：1.平行关系；2.垂直关系.7.【考点】函数的零点；函数奇偶性的判断．【分析】利用函数奇偶性的判断一件零点的定义分别分...