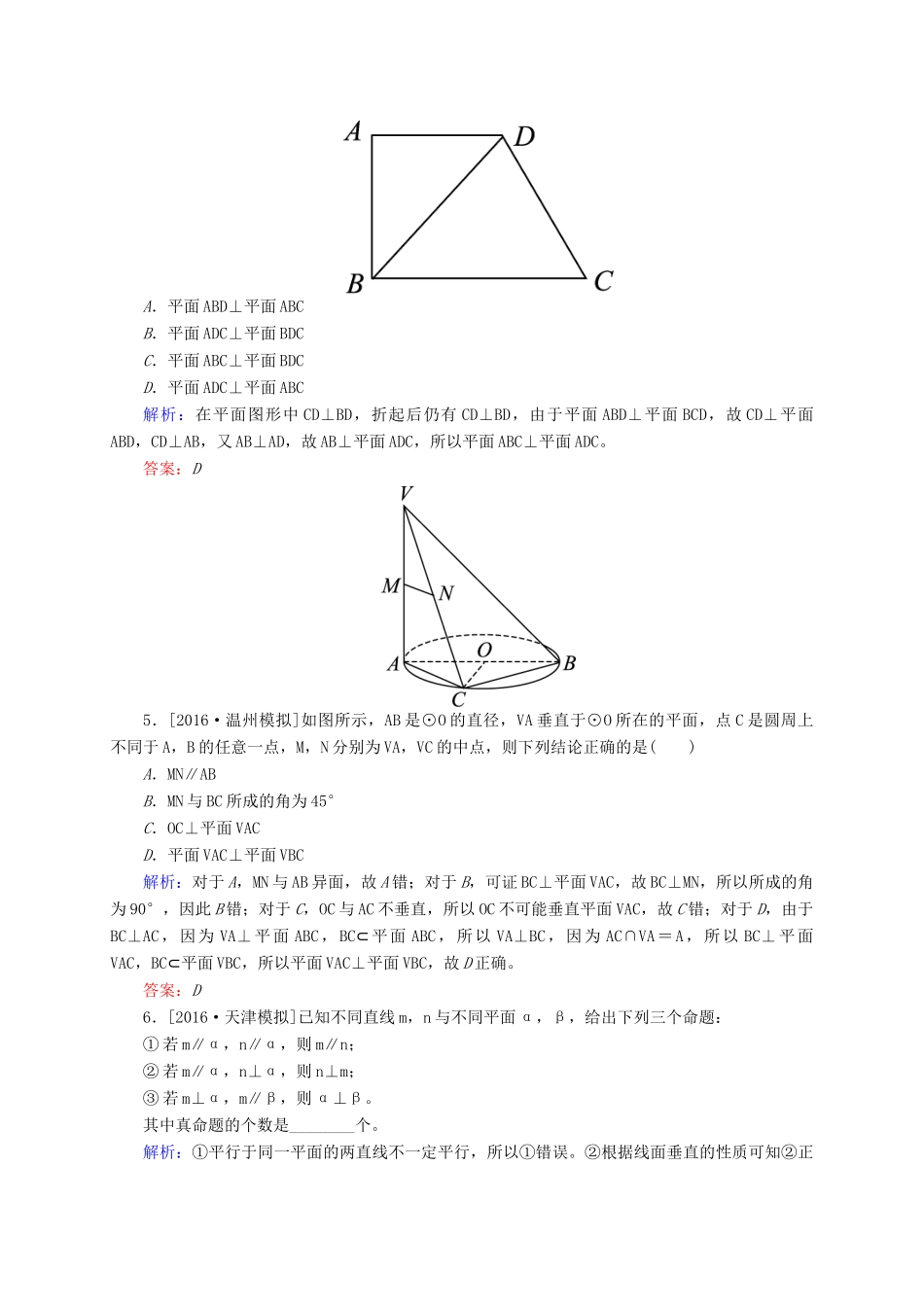
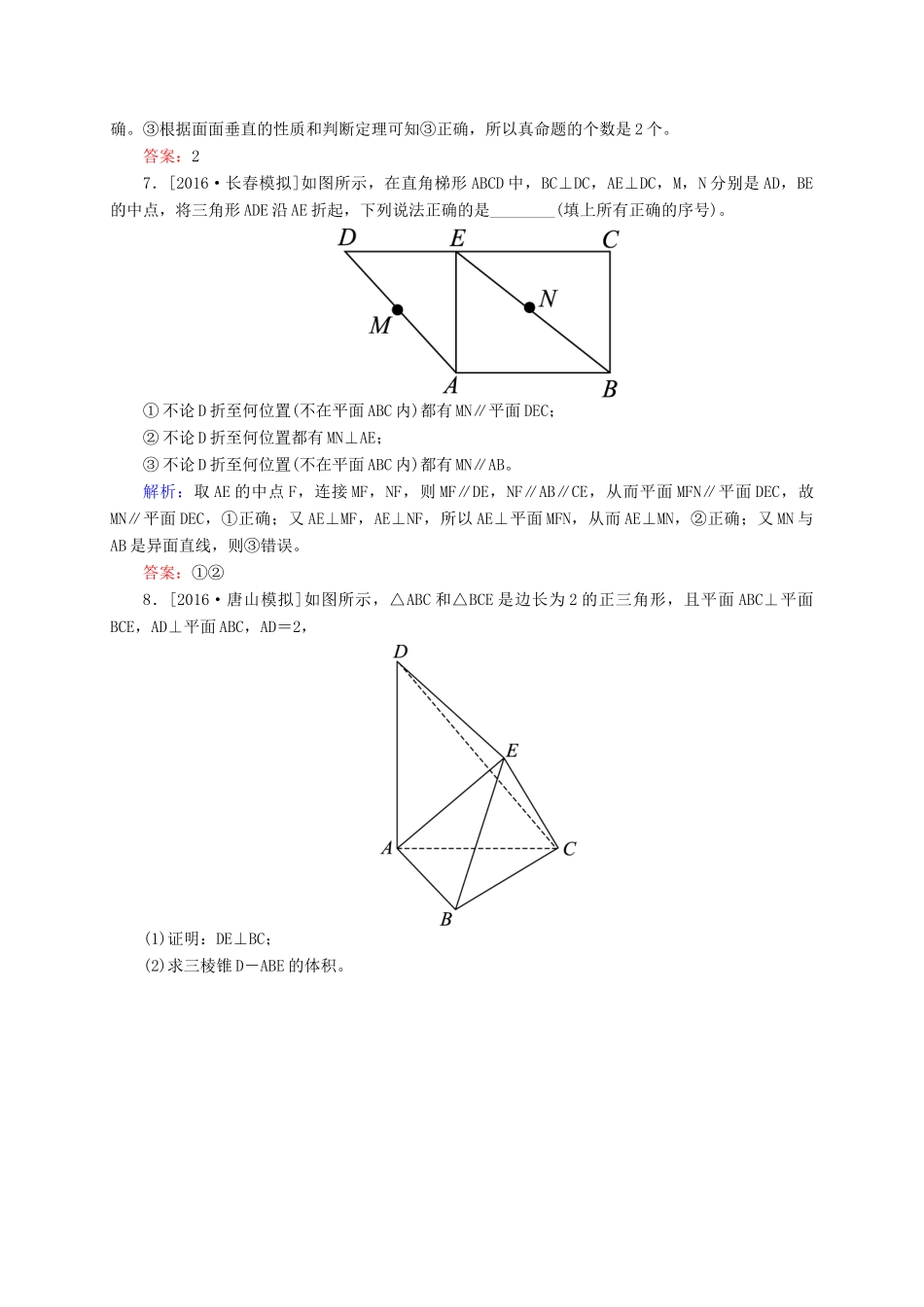
开卷速查(四十四)直线、平面垂直的判定及其性质A级基础巩固练1.[2014·浙江]设m,n是两条不同的直线,α,β是两个不同的平面。()A.若m⊥n,n∥α,则m⊥αB.若m∥β,β⊥α,则m⊥αC.若m⊥β,n⊥β,n⊥α,则m⊥αD.若m⊥n,n⊥β,β⊥α,则m⊥α解析:选项A、B、D中m均可能与平面α平行、垂直、斜交或在平面α内,故选C。答案:C2.[2016·珠海模拟]在空间中,l,m,n,a,b表示直线,α表示平面,则下列命题正确的是()A.若l∥α,m⊥l,则m⊥αB.若l⊥m,m⊥n,则m∥nC.若a⊥α,a⊥b,则b∥αD.若l⊥α,l∥a,则a⊥α解析:对于A,m与α位置关系不确定,故A错,对于B,当l与m,m与n为异面垂直时,m与n可能异面或相交,故B错,对于C,也可能b⊂α,故C错,对于D,由线面垂直的定义可知正确。答案:D3.如图,在斜三棱柱ABC-A1B1C1中,∠BAC=90°,BC1⊥AC,则C1在底面ABC上的射影H必在()A.直线AB上B.直线BC上C.直线AC上D.△ABC内部解析:由AC⊥AB,AC⊥BC1,∴AC⊥平面ABC1。又 AC⊂面ABC,∴平面ABC1⊥平面ABC。∴C1在面ABC上的射影H必在两平面交线AB上。答案:A4.如图,在四边形ABCD中,AD∥BC,AD=AB,∠BCD=45°,∠BAD=90°,将△ABD沿BD折起,使平面ABD⊥平面BCD,构成三棱锥A-BCD,则在三棱锥A-BCD中,下面命题正确的是()A.平面ABD⊥平面ABCB.平面ADC⊥平面BDCC.平面ABC⊥平面BDCD.平面ADC⊥平面ABC解析:在平面图形中CD⊥BD,折起后仍有CD⊥BD,由于平面ABD⊥平面BCD,故CD⊥平面ABD,CD⊥AB,又AB⊥AD,故AB⊥平面ADC,所以平面ABC⊥平面ADC。答案:D5.[2016·温州模拟]如图所示,AB是⊙O的直径,VA垂直于⊙O所在的平面,点C是圆周上不同于A,B的任意一点,M,N分别为VA,VC的中点,则下列结论正确的是()A.MN∥ABB.MN与BC所成的角为45°C.OC⊥平面VACD.平面VAC⊥平面VBC解析:对于A,MN与AB异面,故A错;对于B,可证BC⊥平面VAC,故BC⊥MN,所以所成的角为90°,因此B错;对于C,OC与AC不垂直,所以OC不可能垂直平面VAC,故C错;对于D,由于BC⊥AC,因为VA⊥平面ABC,BC⊂平面ABC,所以VA⊥BC,因为AC∩VA=A,所以BC⊥平面VAC,BC⊂平面VBC,所以平面VAC⊥平面VBC,故D正确。答案:D6.[2016·天津模拟]已知不同直线m,n与不同平面α,β,给出下列三个命题:①若m∥α,n∥α,则m∥n;②若m∥α,n⊥α,则n⊥m;③若m⊥α,m∥β,则α⊥β。其中真命题的个数是________个。解析:①平行于同一平面的两直线不一定平行,所以①错误。②根据线面垂直的性质可知②正确。③根据面面垂直的性质和判断定理可知③正确,所以真命题的个数是2个。答案:27.[2016·长春模拟]如图所示,在直角梯形ABCD中,BC⊥DC,AE⊥DC,M,N分别是AD,BE的中点,将三角形ADE沿AE折起,下列说法正确的是________(填上所有正确的序号)。①不论D折至何位置(不在平面ABC内)都有MN∥平面DEC;②不论D折至何位置都有MN⊥AE;③不论D折至何位置(不在平面ABC内)都有MN∥AB。解析:取AE的中点F,连接MF,NF,则MF∥DE,NF∥AB∥CE,从而平面MFN∥平面DEC,故MN∥平面DEC,①正确;又AE⊥MF,AE⊥NF,所以AE⊥平面MFN,从而AE⊥MN,②正确;又MN与AB是异面直线,则③错误。答案:①②8.[2016·唐山模拟]如图所示,△ABC和△BCE是边长为2的正三角形,且平面ABC⊥平面BCE,AD⊥平面ABC,AD=2,(1)证明:DE⊥BC;(2)求三棱锥D-ABE的体积。解析:(1)证明:取BC的中点为F,连接AF,EF,BD,因为△BCE是正三角形,所以EF⊥BC,又平面ABC⊥平面BCE,且交线为BC,所以EF⊥平面ABC,又AD⊥平面ABC,所以AD∥EF,所以D,A,F,E共面,又易知在正三角形ABC中,AF⊥BC,AF∩EF=F,所以BC⊥平面DAFE,又DE⊂平面DAFE,故DE⊥BC。(2)由(1)知EF∥AD,所以有VD-ABE=VE-DAB=VF-DAB=VD-ABF,而S△ABF=BF·AF=。所以VD-ABF=S△ABF·AD=1,即VD-ABE=1。B级能力提升练9.如图,在正方体ABCD-A1B1C1D1中,E为棱C1D1的中点,F为棱BC的中点。(1)求证:AE⊥DA1;(2)在线段AA1上求一点G,使得直线AE⊥平面DFG。解析:(1)证明:连接AD1,BC1,由正方体的性质可知,DA1...