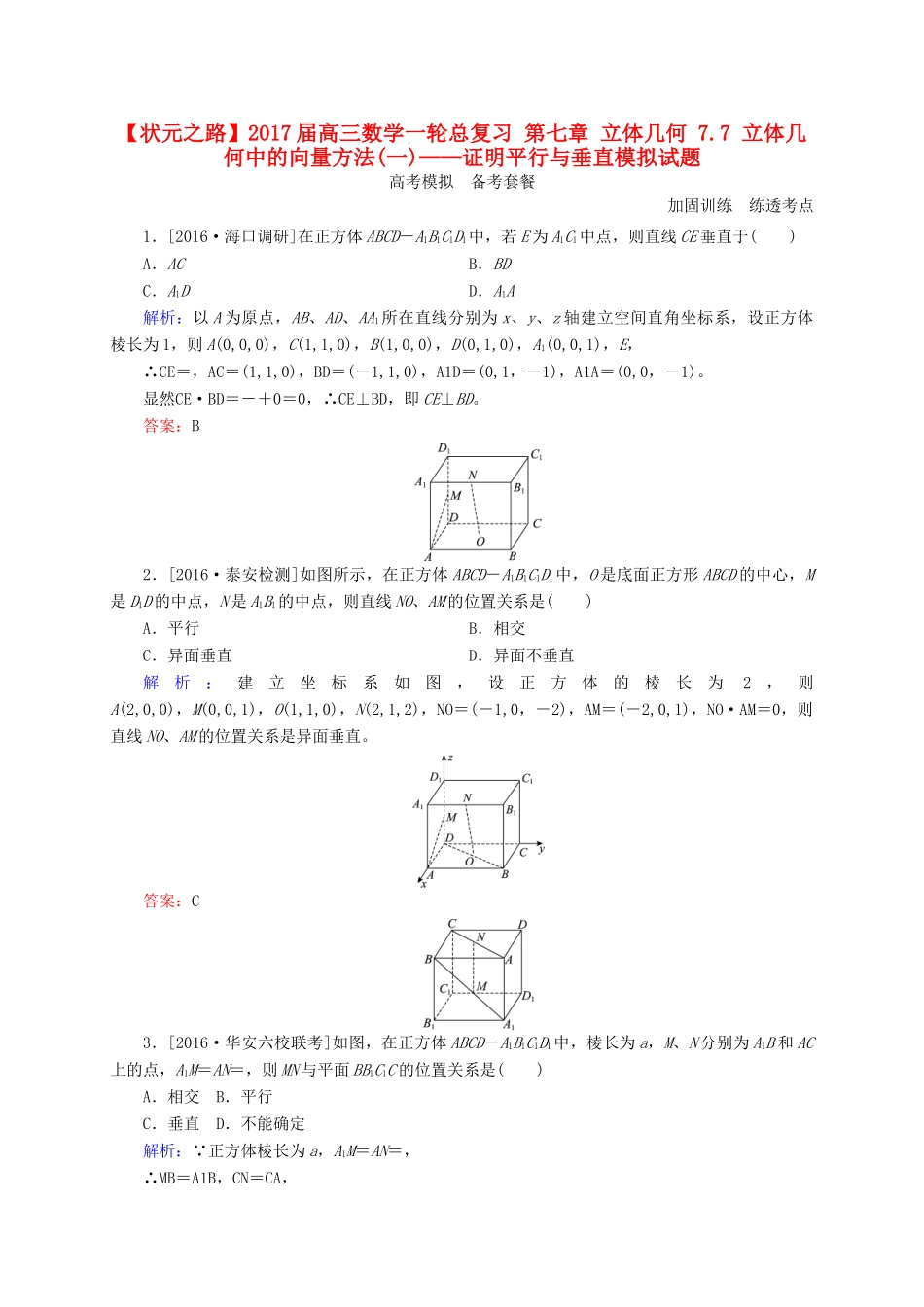
【状元之路】2017届高三数学一轮总复习第七章立体几何7.7立体几何中的向量方法(一)——证明平行与垂直模拟试题高考模拟备考套餐加固训练练透考点1.[2016·海口调研]在正方体ABCD-A1B1C1D1中,若E为A1C1中点,则直线CE垂直于()A.ACB.BDC.A1DD.A1A解析:以A为原点,AB、AD、AA1所在直线分别为x、y、z轴建立空间直角坐标系,设正方体棱长为1,则A(0,0,0),C(1,1,0),B(1,0,0),D(0,1,0),A1(0,0,1),E,∴CE=,AC=(1,1,0),BD=(-1,1,0),A1D=(0,1,-1),A1A=(0,0,-1)。显然CE·BD=-+0=0,∴CE⊥BD,即CE⊥BD。答案:B2.[2016·泰安检测]如图所示,在正方体ABCD-A1B1C1D1中,O是底面正方形ABCD的中心,M是D1D的中点,N是A1B1的中点,则直线NO、AM的位置关系是()A.平行B.相交C.异面垂直D.异面不垂直解析:建立坐标系如图,设正方体的棱长为2,则A(2,0,0),M(0,0,1),O(1,1,0),N(2,1,2),NO=(-1,0,-2),AM=(-2,0,1),NO·AM=0,则直线NO、AM的位置关系是异面垂直。答案:C3.[2016·华安六校联考]如图,在正方体ABCD-A1B1C1D1中,棱长为a,M、N分别为A1B和AC上的点,A1M=AN=,则MN与平面BB1C1C的位置关系是()A.相交B.平行C.垂直D.不能确定解析:∵正方体棱长为a,A1M=AN=,∴MB=A1B,CN=CA,∴MN=MB+BC+CN=A1B+BC+CA=(A1B1+B1B)+BC+(CD+DA)=B1B+B1C1。又∵CD是平面B1BCC1的法向量,且MN·CD=·CD=0,∴MN⊥CD,∴MN∥平面B1BCC1。答案:B4.[2016·苏州调研]如图,已知直三棱柱ABC-A1B1C1中,AC⊥BC,D为AB的中点,AC=BC=BB1。求证:(1)BC1⊥AB1;(2)BC1∥平面CA1D。证明:如图,以C1点为原点,C1A1,C1B1,C1C所在直线分别为x轴、y轴、z轴建立空间直角坐标系。设AC=BC=BB1=2,则A(2,0,2),B(0,2,2),C(0,0,2),A1(2,0,0),B1(0,2,0),C1(0,0,0),D(1,1,2)。(1)由于BC1=(0,-2,-2),AB1=(-2,2,-2),所以BC1·AB1=0-4+4=0,因此BC1⊥AB1,故BC1⊥AB1。(2)连接A1C,取A1C的中点E,连接DE,由于E(1,0,1),所以ED=(0,1,1),又BC1=(0,-2,-2),所以ED=-BC1,又ED和BC1不共线,所以ED∥BC1,又DE⊂平面CA1D,BC1⊄平面CA1D,故BC1∥平面CA1D。