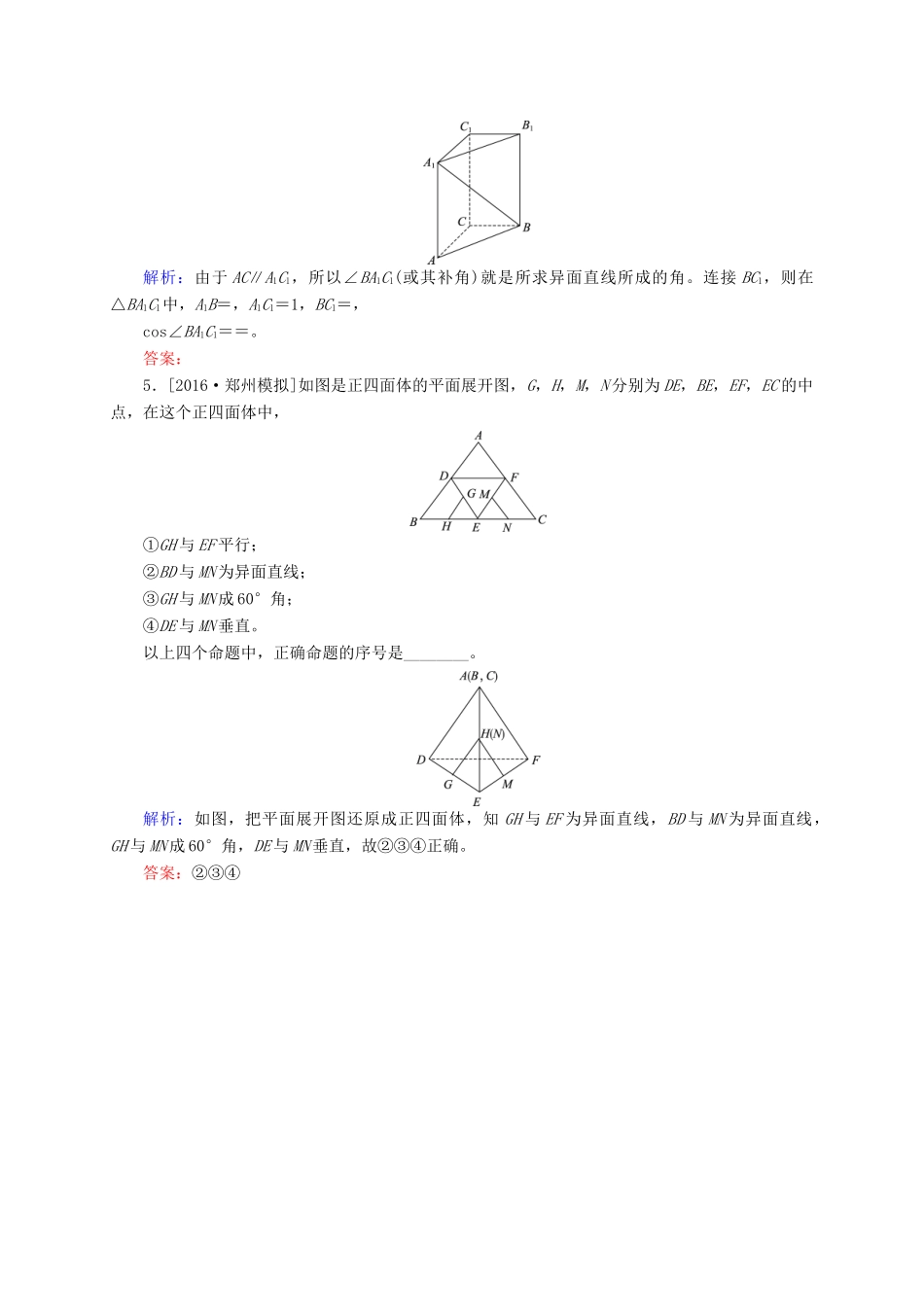
【状元之路】2017届高三数学一轮总复习第七章立体几何7.3空间点、直线、平面之间的位置关系模拟试题高考模拟备考套餐加固训练练透考点1.[2015·浙江]设α,β是两个不同的平面,l,m是两条不同的直线,且l⊂α,m⊂β。()A.若l⊥β,则α⊥βB.若α⊥β,则l⊥mC.若l∥β,则α∥βD.若α∥β,则l∥m解析:对于面面垂直的判定,主要是两个条件,即l⊂α,l⊥β,如果这两个条件存在,则α⊥β。答案:A2.[2015·广东]若直线l1和l2是异面直线,l1在平面α内,l2在平面β内,l是平面α与平面β的交线,则下列命题正确的是()A.l与l1,l2都不相交B.l与l1,l2都相交C.l至多与l1,l2中的一条相交D.l至少与l1,l2中的一条相交解析:可用反证法。假设l与l1,l2都不相交,因为l与l1都在平面α内,于是l∥l1;同理l∥l2,于是l1∥l2,与已知矛盾,故l至少与l1,l2中的一条相交。答案:D3.[2016·临沂模拟]在三棱锥S-ACB中,∠SAB=∠SAC=∠ACB=90°,AC=2,BC=,SB=,则SC与AB所成角的余弦值为________。解析:如图,取BC的中点E,分别在平面ABC内作DE∥AB,在平面SBC内作EF∥SC,则异面直线SC与AB所成的角为∠FED,过F作FG⊥AB,连接DG,则△DFG为直角三角形。由题知AC=2,BC=,SB=,可得DE=,EF=2,DF=。在△DEF中,由余弦定理可得cos∠FED==。答案:4.[2016·泸州模拟]如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,AA1=2,AC=BC=1,则异面直线A1B与AC所成角的余弦值为________。解析:由于AC∥A1C1,所以∠BA1C1(或其补角)就是所求异面直线所成的角。连接BC1,则在△BA1C1中,A1B=,A1C1=1,BC1=,cos∠BA1C1==。答案:5.[2016·郑州模拟]如图是正四面体的平面展开图,G,H,M,N分别为DE,BE,EF,EC的中点,在这个正四面体中,①GH与EF平行;②BD与MN为异面直线;③GH与MN成60°角;④DE与MN垂直。以上四个命题中,正确命题的序号是________。解析:如图,把平面展开图还原成正四面体,知GH与EF为异面直线,BD与MN为异面直线,GH与MN成60°角,DE与MN垂直,故②③④正确。答案:②③④