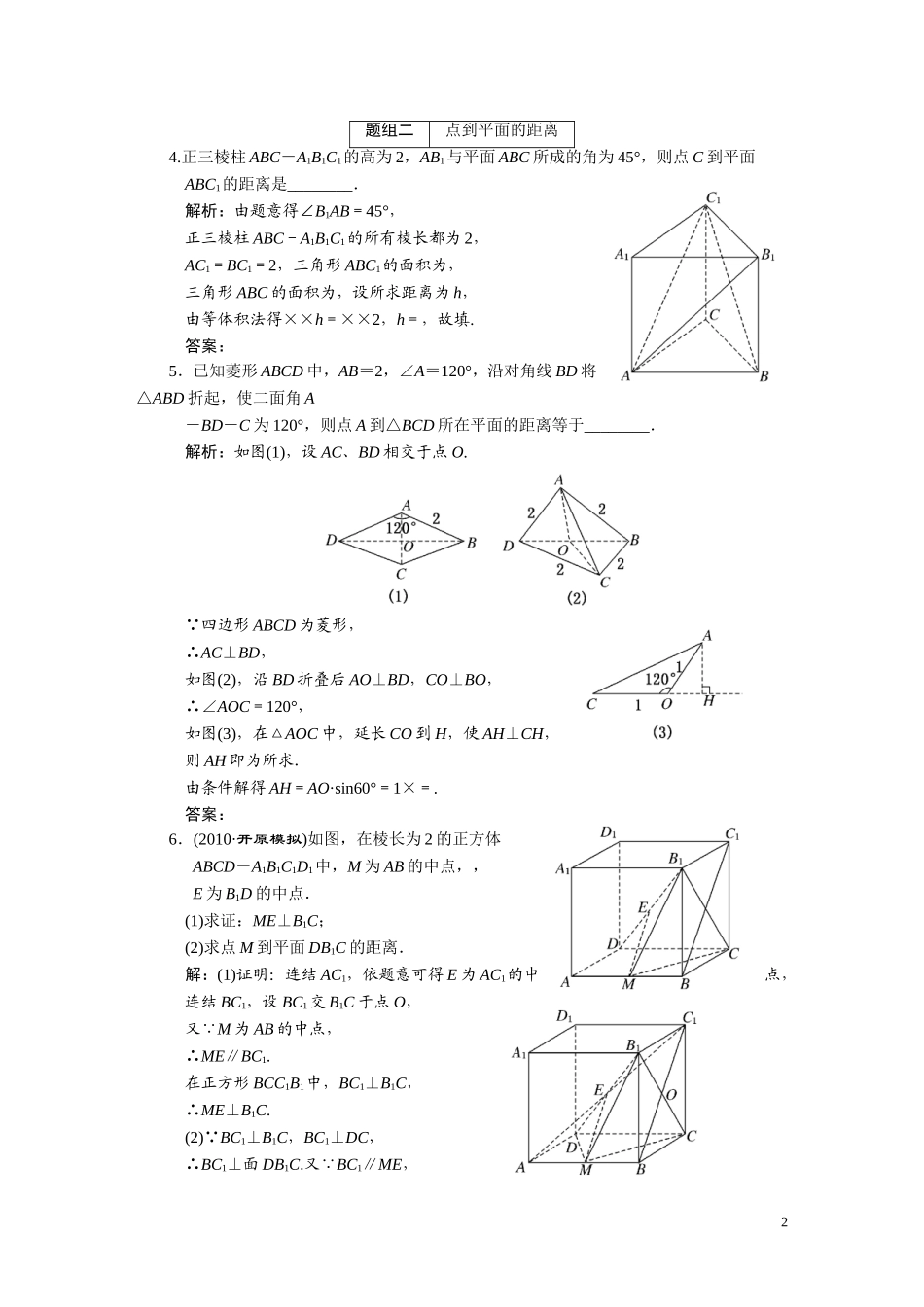
第九章第五节空间距离题组一两点间的距离、点到直线的距离1.侧棱长为2的正三棱锥,若高为1,则该正三棱锥的底面周长是()A.6B.9C.12D.18解析:如图,P-ABC是正三棱锥,PA=2,作PO⊥平面ABC.连结AO并延长交BC于D. PO=1,∴AO==.∴AD=AO=,又AD=AB,∴AB=AD=3.∴底面周长是9.答案:B2.在△ABC中,AB=AC=5,BC=6,PA⊥平面ABC,PA=8,则P到BC的距离是()A.B.2C.3D.4解析:取BC的中点O,连结AO,PO,则BC⊥AO. PA⊥BC,PA∩AO=A,∴BC⊥平面PAO.又PO⊂平面PAO,∴BC⊥PO,∴线段PO的长即为P到BC的距离,在Rt△ABO中,AO==4,在Rt△PAO中,PO==4.答案:D3.设P是60°的二面角α-l-β内一点,PA⊥α,PB⊥β,A、B分别为垂足,PA=2,PB=4,则AB的长是________.解析:如图所示,PA与PB确定平面γ,与l交于点E,则BE⊥l,AE⊥l,∴∠BEA即为二面角的平面角,∴∠BEA=60°,从而∠BPA=120°,∴AB===2.答案:21题组二点到平面的距离4.正三棱柱ABC-A1B1C1的高为2,AB1与平面ABC所成的角为45°,则点C到平面ABC1的距离是________.解析:由题意得∠B1AB=45°,正三棱柱ABC-A1B1C1的所有棱长都为2,AC1=BC1=2,三角形ABC1的面积为,三角形ABC的面积为,设所求距离为h,由等体积法得××h=××2,h=,故填.答案:5.已知菱形ABCD中,AB=2,∠A=120°,沿对角线BD将△ABD折起,使二面角A-BD-C为120°,则点A到△BCD所在平面的距离等于________.解析:如图(1),设AC、BD相交于点O. 四边形ABCD为菱形,∴AC⊥BD,如图(2),沿BD折叠后AO⊥BD,CO⊥BO,∴∠AOC=120°,如图(3),在△AOC中,延长CO到H,使AH⊥CH,则AH即为所求.由条件解得AH=AO·sin60°=1×=.答案:6.(2010·开原模拟)如图,在棱长为2的正方体ABCD-A1B1C1D1中,M为AB的中点,,E为B1D的中点.(1)求证:ME⊥B1C;(2)求点M到平面DB1C的距离.解:(1)证明:连结AC1,依题意可得E为AC1的中点,连结BC1,设BC1交B1C于点O,又 M为AB的中点,∴ME∥BC1.在正方形BCC1B1中,BC1⊥B1C,∴ME⊥B1C.(2) BC1⊥B1C,BC1⊥DC,∴BC1⊥面DB1C.又 BC1∥ME,2∴ME⊥面DB1C,∴ME为所求距离.又 正方体的棱长为2,∴BC1=2,ME=BC1=.因此,点M到平面DB1C的距离为.(也可由体积相等VM-DB1C=VB1-MDC,求得距离为).题组三直线与平面、平面与平面的距离7.(2009·北京高考)若正四棱柱ABCD-A1B1C1D1的底面边长为1,AB1与底面ABCD成60°角,则A1C1到底面ABCD的距离为()A.B.1C.D.解析:依题可知∠B1AB=60°,平面A1B1C1D1∥平面ABCD,A1C1⊂平面A1B1C1D1,所以B1B即为A1C1到底面ABCD的距离.B1B=.答案:D8.如图所示,在正方体ABCD-A1B1C1D1中,M、E、F、N分别是棱A1B1、B1C1、C1D1、D1A1的中点.(1)求证:平面AMN∥平面EFDB;(2)设AB=1,求平面AMN与平面EFDB间的距离.解:(1)证明:连结MF. M、F是A1B1、C1D1的中点,四边形A1B1C1D1为正方形,∴MF綊A1D1.又A1D1綊AD,∴MF綊AD.∴四边形AMFD是平行四边形.∴AM∥DF. DF⊂平面EFDB,AM⊄平面EFDB,∴AM∥平面EFDB,同理,AN∥平面EFDB.又AM、AN⊂平面AMN,AM∩AN=A,∴平面AMN∥平面EFDB.(2)如图甲所示,分别取棱BB1、CC1的中点Q、P,连结A1Q、A1P、PQ, PQ∥BC,BC⊥平面ABB1A1,∴PQ⊥平面ABB1A1. M为A1B1的中点,3∴AM⊥A1Q.∴A1P⊥AM,同理A1P⊥AN.又AM、AN⊂平面AMN,AM∩AN=A,∴A1P⊥平面AMN.由(1),知平面AMN∥平面EFDB,∴A1P⊥平面EFDB.设A1P与这两个平行平面分别交于点O1,O2,则O1O2的长为两平行平面之间的距离,在平行四边形AA2A3A4中,如图乙.由AA1=1,A2A3=,得AA2=,由等面积法可得O1O2=.题组四距离的综合应用9.(2009·重庆高考)在正四棱柱ABCD-A1B1C1D1中,顶点B1到对角线BD1和到平面A1BCD1的距离分别为h和d,则下列命题中正确的是()A.若侧棱的长小于底面的边长,则的取值范围为(0,1)B.若侧棱的长小于底面的边长,则的取值范围为(,)C.若侧棱的长大于底面的边长,则的取值范围为(,)D.若侧棱的长大于底面的边长,则的取值范围为(,+∞)解析:设正四棱柱底面边长为a,高为b,如图,B1到平面A1BCD1的距...