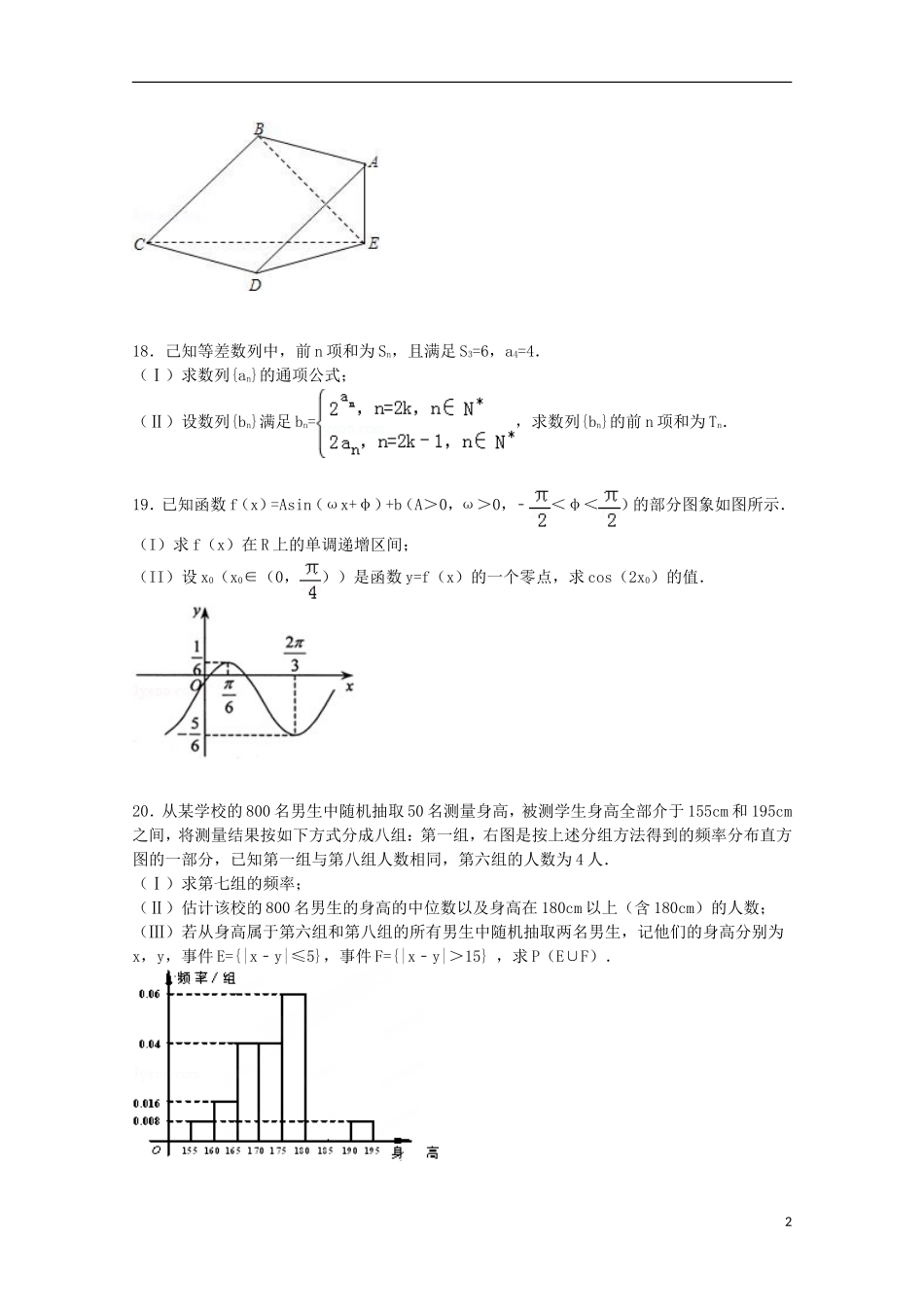
2015年福建省莆田一中高考数学考前模拟试卷(文科)一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题意要求的.1.已知i为虚数单位,a∈R,若为纯虚数,则复数z=(2a+1)+i的模为()A.B.C.D.2.已知集合A={x|2x2﹣x﹣1≥0},B={x|y=},则A∩B=()A.(0,1)B.(0,1]C.(1,+∞)D.上存在x1,x2(a<x1<x2<b)满足f′(x1)=,f′(x2),则称函数f(x)是上的“双中值函数”.已知函数f(x)=x3﹣x2+a是上“双中值函数”,则实数a的取值范围是()A.(,)B.(0,1)C.(,1)D.(,1)二、填空题:本大题共4小题,每小题4分,共16分,将答案填在题后的横线上.13.某单位有840名职工,现采用系统抽样抽取42人做问卷调查,将840人按1,2,…,840随机编号,则抽取的42人中,编号落入区间的人数为.14.设奇函数f(x)的定义域为R,且周期为5,若f(1)=﹣1,f(4)=log2a,则a=.15.已知双曲线=1(a>0,b>0)的右焦点为F,过F作斜率为﹣1的直线交双曲线的渐近线于点P,点P在第一象限,O为坐标原点,若△OFP的面积为,则该双曲线的离心率为.16.已知数列{an}满足a1=1,an=logn(n+1)(n≥2,n∈N*).定义:使乘积a1•a2…ak为正整数的k(k∈N*)叫做“易整数”.则在内所有“易整数”的和为.三.解答题:本大题共6小题,共74分,解答应写出文字说明、证明过程或演算过程17.如图,正方形ABCD所在平面与三角形CDE所在平面相交于CD,AE⊥平面CDE,且AE=3,AB=6.(1)求证:AB⊥平面ADE;(2)求凸多面体ABCDE的体积.118.己知等差数列中,前n项和为Sn,且满足S3=6,a4=4.(Ⅰ)求数列{an}的通项公式;(Ⅱ)设数列{bn}满足bn=,求数列{bn}的前n项和为Tn.19.已知函数f(x)=Asin(ωx+φ)+b(A>0,ω>0,﹣<φ<)的部分图象如图所示.(I)求f(x)在R上的单调递增区间;(II)设x0(x0∈(0,))是函数y=f(x)的一个零点,求cos(2x0)的值.20.从某学校的800名男生中随机抽取50名测量身高,被测学生身高全部介于155cm和195cm之间,将测量结果按如下方式分成八组:第一组,右图是按上述分组方法得到的频率分布直方图的一部分,已知第一组与第八组人数相同,第六组的人数为4人.(Ⅰ)求第七组的频率;(Ⅱ)估计该校的800名男生的身高的中位数以及身高在180cm以上(含180cm)的人数;(Ⅲ)若从身高属于第六组和第八组的所有男生中随机抽取两名男生,记他们的身高分别为x,y,事件E={|x﹣y|≤5},事件F={|x﹣y|>15},求P(E∪F).221.如图,在平面直角坐标系xoy中,椭圆C:=1(a>b>0)的离心率为,直线l与x轴交于点E,与椭圆C交于A、B两点.当直线l垂直于x轴且点E为椭圆C的右焦点时,弦AB的长为.(1)求椭圆C的方程;(2)是否存在点E,使得为定值?若存在,请指出点E的坐标,并求出该定值;若不存在,请说明理由.22.已知t>0,设函数f(x)=x3﹣+3tx+1.(Ⅰ)若f(x)在(0,2)上无极值,求t的值;(Ⅱ)若存在x0∈(0,2),使得f(x0)是f(x)在上的最大值,求t的取值范围;(Ⅲ)若f(x)≤xex﹣m+2(e为自然对数的底数)对任意x∈C.(1,+∞)D.上存在x1,x2(a<x1<x2<b)满足f′(x1)=,f′(x2),则称函数f(x)是上的“双中值函数”.已知函数f(x)=x3﹣x2+a是上“双中值函数”,则实数a的取值范围是()A.(,)B.(0,1)C.(,1)D.(,1)考点:函数的单调性与导数的关系;变化的快慢与变化率.专题:导数的综合应用.分析:由新定义可知f′(x1)=f′(x2)=a2﹣a,即方程3x2﹣2x=a2﹣a在区间(0,a)有两个解,利用二次函数的性质可知实数a的取值范围解答:解:由题意可知,在区间存在x1,x2(0<x1<x2<a),满足f′(x1)===a2﹣a, f(x)=x3﹣x2+a,∴f′(x)=3x2﹣2x,3∴方程3x2﹣2x=a2﹣a在区间(0,a)有两个解.令g(x)=3x2﹣2x﹣a2+a,(0<x<a),∴解得<a<1,故选:D.点评:本题主要考查了导数的几何意义,二次函数的性质与方程根的关系,属于中档题二、填空题:本大题共4小题,每小题4分,共16分,将答案填在题后的横线上.13.某单位有...