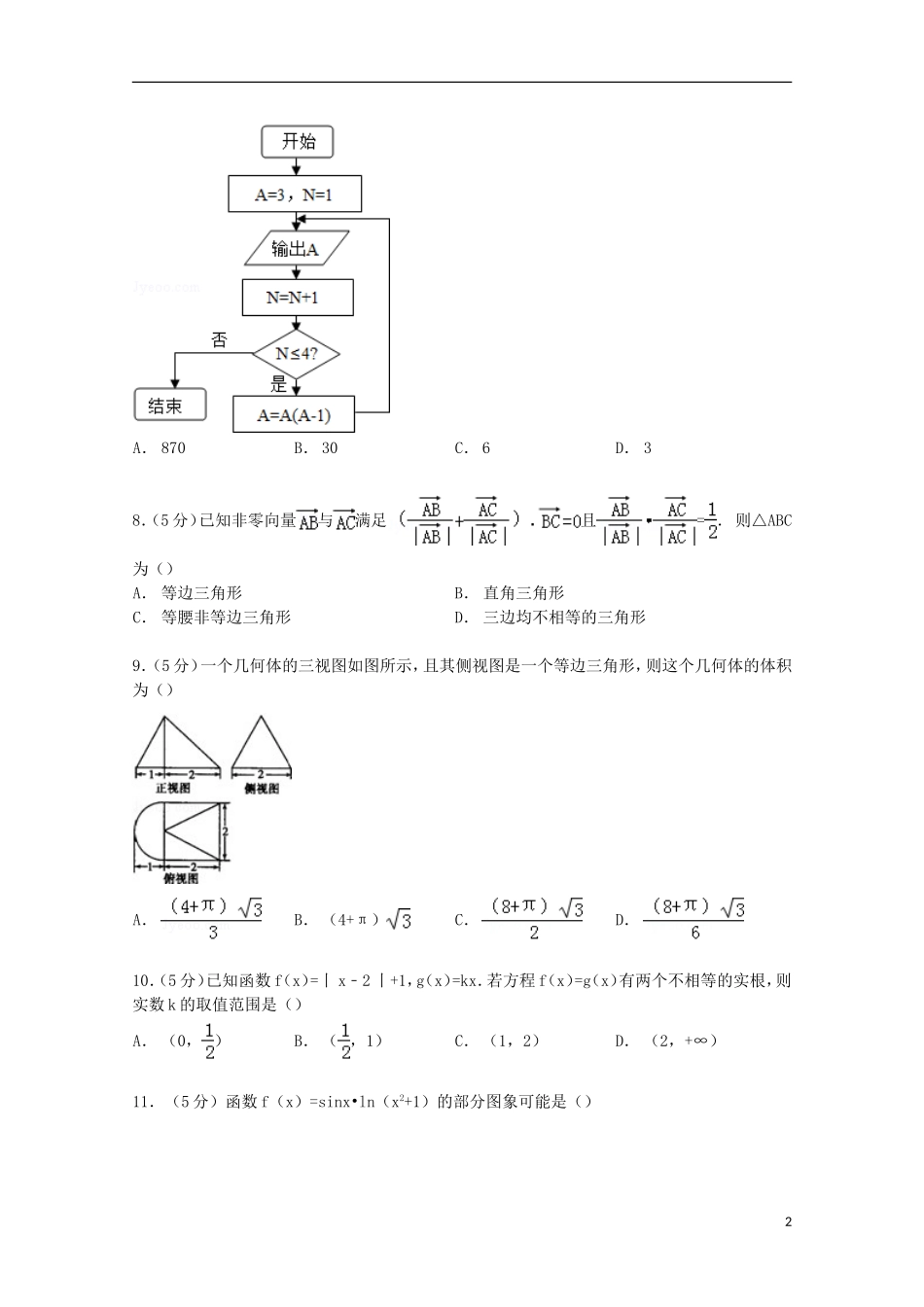
甘肃省兰州市西北师大附中2015届高三上学期12月月考数学试卷(理科)一、选择题(本大题共12个小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)1.(5分)如果(3+i)z=10i(其中i2=﹣1),则复数z的共轭复数为()A.﹣1+3iB.1﹣3iC.1+3iD.﹣1﹣3i2.(5分)已知集合A={x|x>1},B={x|x2﹣2x<0},则A∩B=()A.{x|x>0}B.{x|x>1}C.{x|1<x<2}D.{x|0<x<2}3.(5分)已知向量=+3,=5+3,=﹣3+3,则()A.A、B、C三点共线B.A、B、D三点共线C.A、C、D三点共线D.B、C、D三点共线4.(5分)若函数f(x)=ax2+bx+c(a,b,c>0)没有零点,则的取值范围是()A.(1,+∞)B.[1,+∞)C.(2,+∞)D.[2,+∞)5.(5分)设f(x)是定义在R上的奇函数,当x<0时,f(x)=x﹣e﹣x(e为自然数的底数),则f(ln6)的值为()A.ln6+6B.ln6﹣6C.﹣ln6+6D.﹣ln6﹣66.(5分)函数y=f(x)的图象如图所示.观察图象可知函数y=f(x)的定义域、值域分别是()A.[﹣5,0]∪[2,6),[0,5]B.[﹣5,6),[0,+∞)C.[﹣5,0]∪[2,6),[0,+∞)D.[﹣5,+∞),[2,5]7.(5分)执行如图所示的程序框图,会输出一列数,则这个数列的第3项是()1A.870B.30C.6D.38.(5分)已知非零向量与满足且=.则△ABC为()A.等边三角形B.直角三角形C.等腰非等边三角形D.三边均不相等的三角形9.(5分)一个几何体的三视图如图所示,且其侧视图是一个等边三角形,则这个几何体的体积为()A.B.(4+π)C.D.10.(5分)已知函数f(x)=丨x﹣2丨+1,g(x)=kx.若方程f(x)=g(x)有两个不相等的实根,则实数k的取值范围是()A.(0,)B.(,1)C.(1,2)D.(2,+∞)11.(5分)函数f(x)=sinx•ln(x2+1)的部分图象可能是()2A.B.C.D.12.(5分)设f(x)是定义在R上的奇函数,且f(2)=0,当x>0时,有恒成立,则不等式x2f(x)>0的解集是()A.(﹣2,0)∪(2,+∞)B.(﹣2,0)∪(0,2)C.(﹣∞,﹣2)∪(2,+∞)D.(﹣∞,﹣2)∪(0,2)二、填空题:本大题共4小题,每小题5分,共20分,把答案填在答题卷的横线上..13.(5分)已知函数f(x)=则f[f()]=.14.(5分)过双曲线的左焦点F(﹣c,0)作圆x2+y2=a2的切线,切点为E,延长FE交抛物线y2=4cx于点P,若E为线段FP的中点,则双曲线的离心率为.15.(5分)已知点A是不等式组所表示的平面区域内的一个动点,点B(﹣2,1),O为坐标原点,则的最大值是.16.(5分)己知函数f(x)=,{an}为a1=1,d=2的等差数列,则f(a1)+f(a2)+f(a3)+…+f(a10)=.三、解答题:解答应写出文字说明、证明过程或演算步骤17.(12分)设函数.(Ⅰ)求f(x)的最大值,并写出使f(x)取最大值是x的集合;(Ⅱ)已知△ABC中,角A,B,C的对边分别为a,b,c.若.求a的最小值.18.(12分)在各项均为正数的等比数列{an}中,a1=2,且2a1,a3,3a2成等差数列.3(Ⅰ)求等比数列{an}的通项公式;(Ⅱ)若数列{bn}满足bn=11﹣2log2an,求数列{bn}的前n项和Tn的最大值.19.(12分)假设关于某设备的使用年限x和所支出的维修费用y(万元)有如下的统计资料:使用年限x23456维修费用y2.23.85.56.57.0若由资料知y对x呈线性相关关系.(1)请画出上表数据的散点图;(2)请根据最小二乘法求出线性回归方程=x+的回归系数,.(3)估计使用年限为10年时,维修费用是多少?b=,a=﹣b.20.(12分)如图,已知四棱锥P﹣ABCD,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E,F分别是BC,PC的中点.(1)证明:AE⊥PD;(2)若PA=AB=2,求二面角E﹣AF﹣C的余弦值.21.(12分)已知函数f(x)=x2+a(x+lnx),x>0,a∈R是常数.(1)求函数y=f(x)的图象在点(1,f(1))处的切线方程;(2)若函数y=f(x)图象上的点都在第一象限,试求常数a的取值范围;(3)证明:∀a∈R,存在ξ∈(1,e),使f′(ξ)=.一、选做题(共1小题,满分10分)22.(10分)选修4﹣1:几何证明选讲如图,已知圆上的,过C点的圆的切线与BA的延长线交于E点.(Ⅰ)证明:∠ACE=∠BCD;(Ⅱ)...