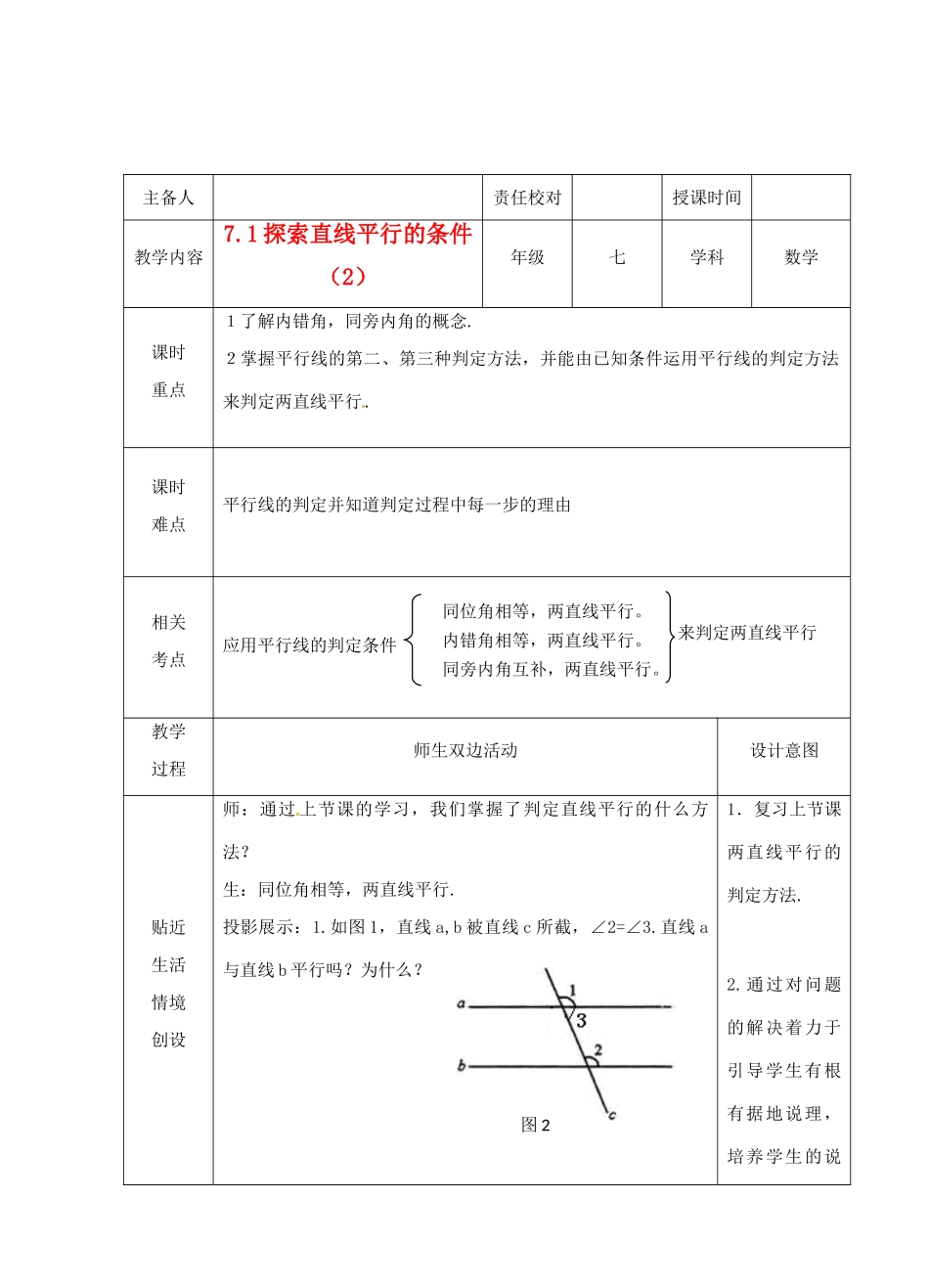
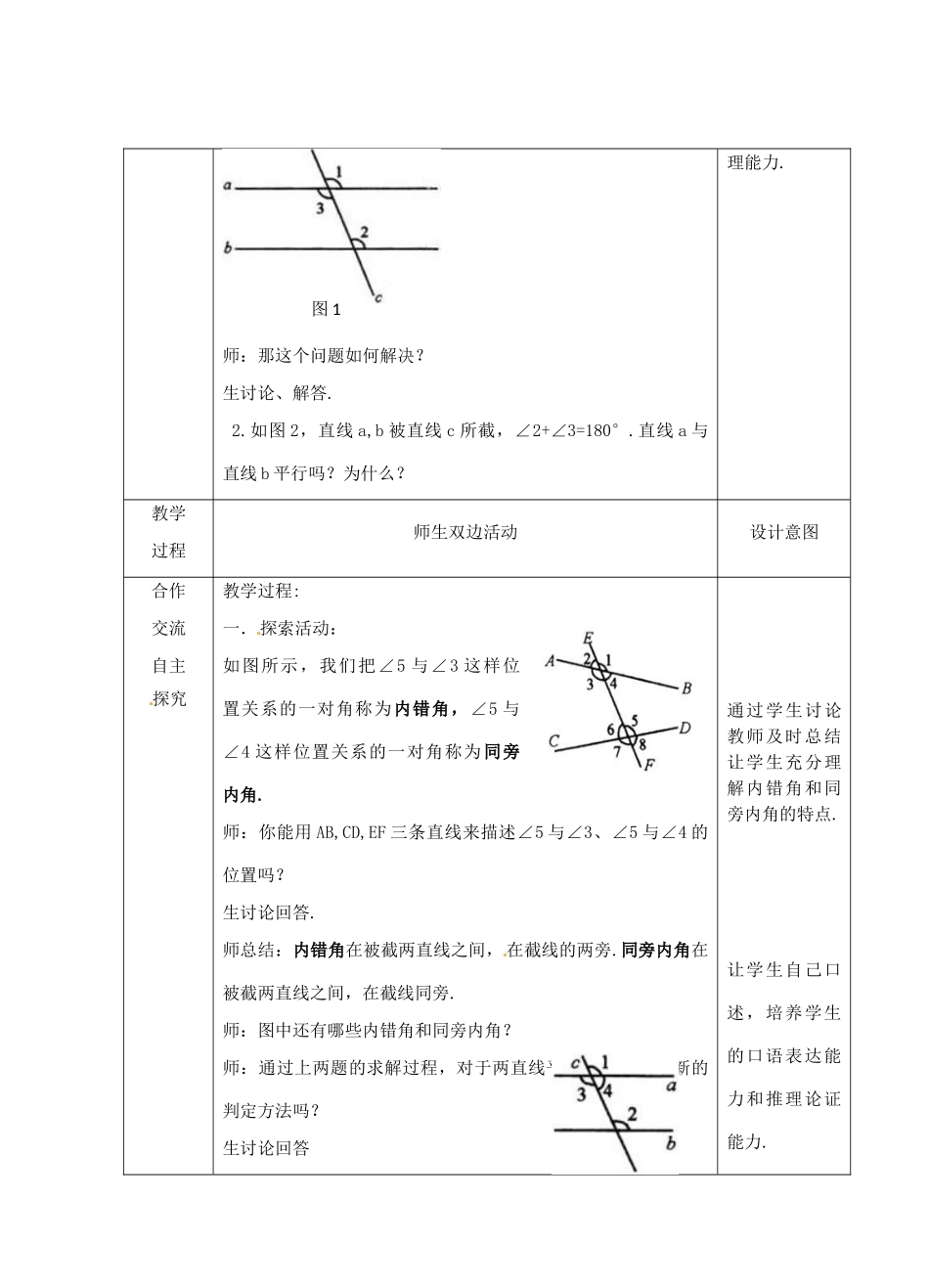
主备人责任校对授课时间教学内容7.1探索直线平行的条件(2)年级七学科数学课时重点1了解内错角,同旁内角的概念.2掌握平行线的第二、第三种判定方法,并能由已知条件运用平行线的判定方法来判定两直线平行.课时难点平行线的判定并知道判定过程中每一步的理由相关考点应用平行线的判定条件教学过程师生双边活动设计意图贴近生活情境创设师:通过上节课的学习,我们掌握了判定直线平行的什么方法?生:同位角相等,两直线平行.投影展示:1.如图1,直线a,b被直线c所截,∠2=∠3.直线a与直线b平行吗?为什么?1.复习上节课两直线平行的判定方法.2.通过对问题的解决着力于引导学生有根有据地说理,培养学生的说同位角相等,两直线平行。内错角相等,两直线平行。同旁内角互补,两直线平行。来判定两直线平行图2师:那这个问题如何解决?生讨论、解答.2.如图2,直线a,b被直线c所截,∠2+∠3=180°.直线a与直线b平行吗?为什么?理能力.教学过程师生双边活动设计意图合作交流自主探究教学过程:一.探索活动:如图所示,我们把∠5与∠3这样位置关系的一对角称为内错角,∠5与∠4这样位置关系的一对角称为同旁内角.师:你能用AB,CD,EF三条直线来描述∠5与∠3、∠5与∠4的位置吗?生讨论回答.师总结:内错角在被截两直线之间,在截线的两旁.同旁内角在被截两直线之间,在截线同旁.师:图中还有哪些内错角和同旁内角?师:通过上两题的求解过程,对于两直线平行,你有什么新的判定方法吗?生讨论回答通过学生讨论教师及时总结让学生充分理解内错角和同旁内角的特点.让学生自己口述,培养学生的口语表达能力和推理论证能力.图1师归纳总结:内错角相等,两直线平行.符号语言:因为∠2=∠3所以a∥b()同旁内角互补,两直线平行.符号语言:因为∠2+∠4=180°所以a∥b()二.例题讲解:例1.如图,∠1=∠2,∠B+∠BDE=180°.图中哪些线互相平行,为什么?解:(1)AB∥CD因为∠1与∠2是AB、EF被DE截成的内错角,且∠1=∠2,所以AB∥CD(2)DE∥BC因为∠B与∠BDE是BC、DE被AB截成的同旁内角,且∠B+∠BDE=180°,所以DE∥BC想一想①∠2与哪个角相等时,DE∥BC?②添加什么条件时使得DE∥BC?③∠B与哪个角相等时,AB∥EF?④添加什么条件时使得AB∥EF?教学过程师生双边活动设计意图合作交流自主三.知识应用1.如图,∠1与∠B,∠3与∠4,∠2与∠4分别是哪两条直线被哪一条直线截成的角?它们分别是什么角?知识应用:注重夯实基础,巩固概念和定理探究2.如图,填空:(1)因为∠1=∠2,所以___∥___;()(2)因为∠2=__,所以AD∥BE;()(3)因为∠1+∠B=180°所以__∥___;()(4)因为∠1+∠__=180°,所以AB∥DE.()3.如图,下列说法中,正确的是()A、因为∠A+∠D=180°,所以AD∥BCB、因为∠C+∠D=180°,所以AB∥CDC、因为∠A+∠D=180°,所以AB∥CDD、因为∠A+∠C=180°,所以AB∥CD4.如图,要得到AB∥CD,只需要添加一个条件,这个条件可以是_________.(填一个你认为正确的条件即可)教学过程师生双边活动设计意图巩固提高运用拓展1.如图,能使BF∥DG的条件是()A、∠1=∠3B、∠2=∠4C、∠2=∠3D、∠1=∠42.如图,AE平分∠BAC,CE平分∠ACD,不能判定AB∥CD的条件是()A、∠1=∠2B、∠1+∠2=90°C、∠3+∠4=90°D∠2+∠3=90°灵活运用所学的判定方法判定两直线平行.板书设计7.1探索直线平行的条件(2)1.内错角概念:内错角在被截两直线之间,在截线的两旁.同旁内角概念:同旁内角在被截两直线之间,在截线同旁.2.平行线的判定方法:3.例题讲解:课后盘点自我反思1.让学生掌握平行线的三种判定方法,并能灵活运用三种方法解决问题.2.对于开放试题应引导学生先确定方法再找对应的角.3.对于知识运用的第4题,学生易错,应充分理解和掌握“三线八角”,同位角,内错角,同旁内角都要“贴”着线.