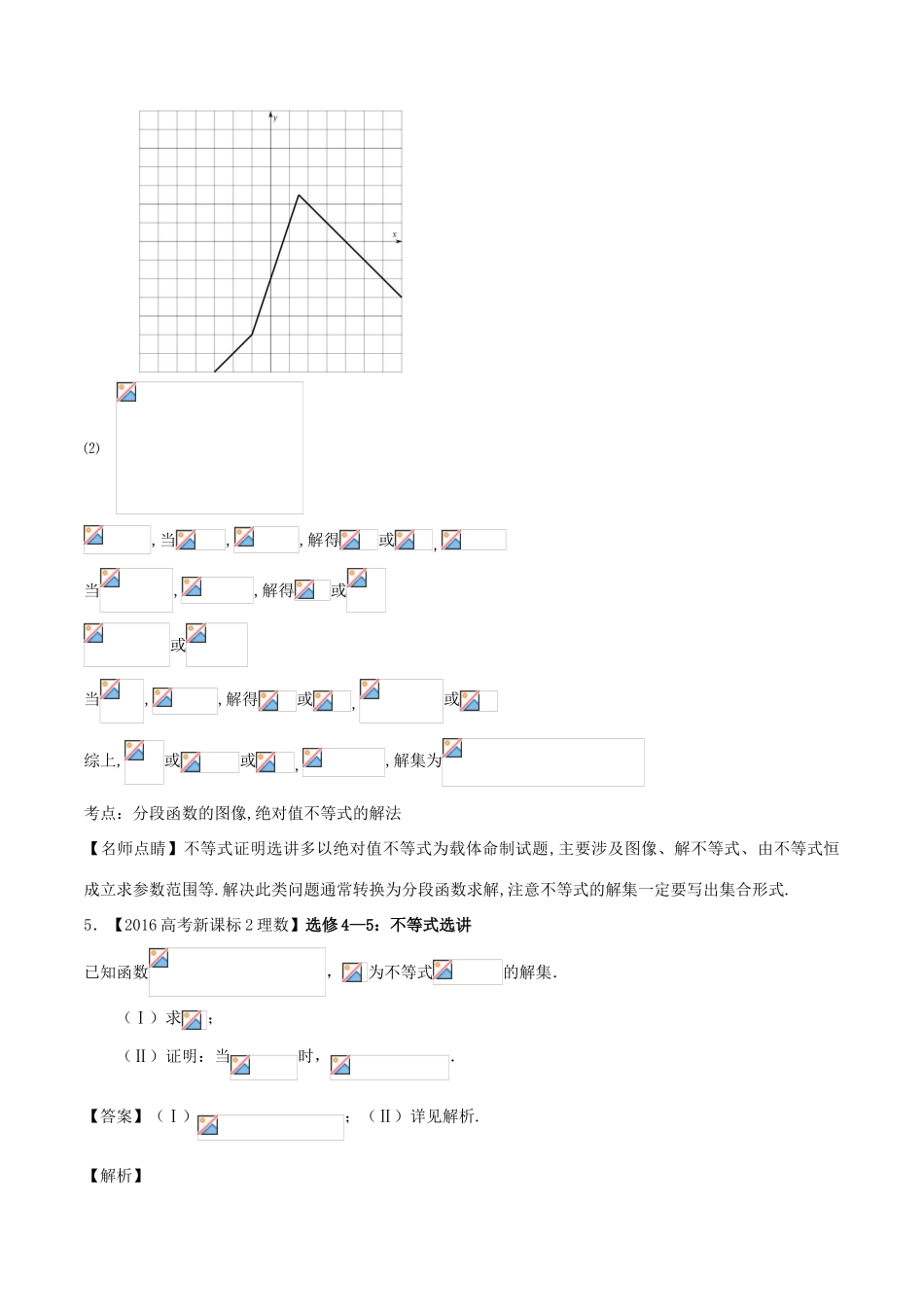
专题4不等式选讲【三年高考】1.【2016高考江苏】设a>0,|x1|<,|y2|<,求证:|2x+y4|<a.【答案】详见解析【考点】含绝对值的不等式证明【名师点睛】利用绝对值三角不等式求最值时,可借助绝对值三角不等式性质定理:||a|-|b||≤|a±b|≤|a|+|b|,通过适当的添、拆项来放缩求解,但一定要注意取等号成立的条件.将绝对值不等式与函数以及不等式恒成立交汇、渗透,解题时强化函数、数形结合与转化与化归思想方法的灵活应用,这是命题的新动向.2.【2015江苏高考,21】解不等式【答案】【解析】【考点定位】含绝对值不等式的解法3.【2014江苏,理21D】[选修4-5:不等式选讲]已知,证明【答案】见解析.【解析】 ,∴,,∴.4.【2016高考新课标1卷】(本小题满分10分),选修4—5:不等式选讲已知函数.(I)在答题卡第(24)题图中画出的图像;(II)求不等式的解集.【答案】(I)见解析(II)【解析】试题分析:(I)取绝对值得分段函数,然后作图;(II)用零点分区间法分,,,分类求解,然后取并集试题解析:⑴如图所示:⑵,当,,解得或,当,,解得或或当,,解得或,或综上,或或,,解集为考点:分段函数的图像,绝对值不等式的解法【名师点睛】不等式证明选讲多以绝对值不等式为载体命制试题,主要涉及图像、解不等式、由不等式恒成立求参数范围等.解决此类问题通常转换为分段函数求解,注意不等式的解集一定要写出集合形式.5.【2016高考新课标2理数】选修4—5:不等式选讲已知函数,为不等式的解集.(Ⅰ)求;(Ⅱ)证明:当时,.【答案】(Ⅰ);(Ⅱ)详见解析.【解析】试题分析:(I)分,和三种情况去掉绝对值,再解不等式,即可得集合;(Ⅱ)采用平方作差法,再进行因式分解,进而可证当,时,确定和的符号,从而证明不等式成立.(II)由(I)知,当时,,从而,因此考点:绝对值不等式,不等式的证明.【名师点睛】形如(或)型的不等式主要有三种解法:(1)分段讨论法:利用绝对值号内式子对应方程的根,将数轴分为,,(此处设)三个部分,在每个部分上去掉绝对值号分别列出对应的不等式求解,然后取各个不等式解集的并集.(2)几何法:利用的几何意义:数轴上到点和的距离之和大于的全体,.(3)图象法:作出函数和的图象,结合图象求解.6.【2015高考新课标2,理24】设均为正数,且,证明:(Ⅰ)若,则;(Ⅱ)是的充要条件.7.【2015高考福建,理21】选修4-5:不等式选讲已知,函数的最小值为4.(Ⅰ)求的值;(Ⅱ)求的最小值.8.【2015高考陕西,理24】选修4-5:不等式选讲已知关于的不等式的解集为.(I)求实数,的值;(II)求的最大值.【解析】(I)由,得,则解得,(II)当且仅当,即时等号成立,故.9.【2015高考新课标1,理24】选修4—5:不等式选讲已知函数=|x+1|-2|x-a|,a>0.(Ⅰ)当a=1时,求不等式f(x)>1的解集;(Ⅱ)若f(x)的图像与x轴围成的三角形面积大于6,求a的取值范围.【解析】(Ⅰ)当a=1时,不等式f(x)>1化为|x+1|-2|x-1|>1,等价于或或,解得,所以不等式f(x)>1的解集为.(Ⅱ)由题设可得,,所以函数的图像与轴围成的三角形的三个顶点分别为,,,所以△ABC的面积为.由题设得>6,解得.所以的取值范围为(2,+∞).10.【2014高考福建理第21(3)题】已知定义在R上的函数的最小值为.(I)求的值;(II)若为正实数,且,求证:.11.【2014高考辽宁理第24题】设函数,,记的解集为M,的解集为N.(Ⅰ)求M;(Ⅱ)当时,证明:.【解析】(Ⅰ),当时,由得,故;当时,由得,故;所以的解集为.(Ⅱ)由得解得,因此,故.当时,,于是,.12.【2014高考全国1第24题】若,且.(Ⅰ)求的最小值;(Ⅱ)是否存在,使得?并说明理由.【解析】(I)由,得,且当时取等号.故,且当时取等号.所以的最小值为.(II)由(I)知,.由于,从而不存在,使得.13.【2014高考全国2第24题】设函数=(Ⅰ)证明:2;(Ⅱ)若,求的取值范围.【2017年高考命题预测】纵观2016各地高考试题,对不等式选讲的考查,主要考查绝对值不等式,柯西不等式,基本不等式等知识,主要考查绝对值不等式的解法,绝对值不等式的最值,绝对值不等式的恒成立问题,利用柯西不等式,基本不等式求最...