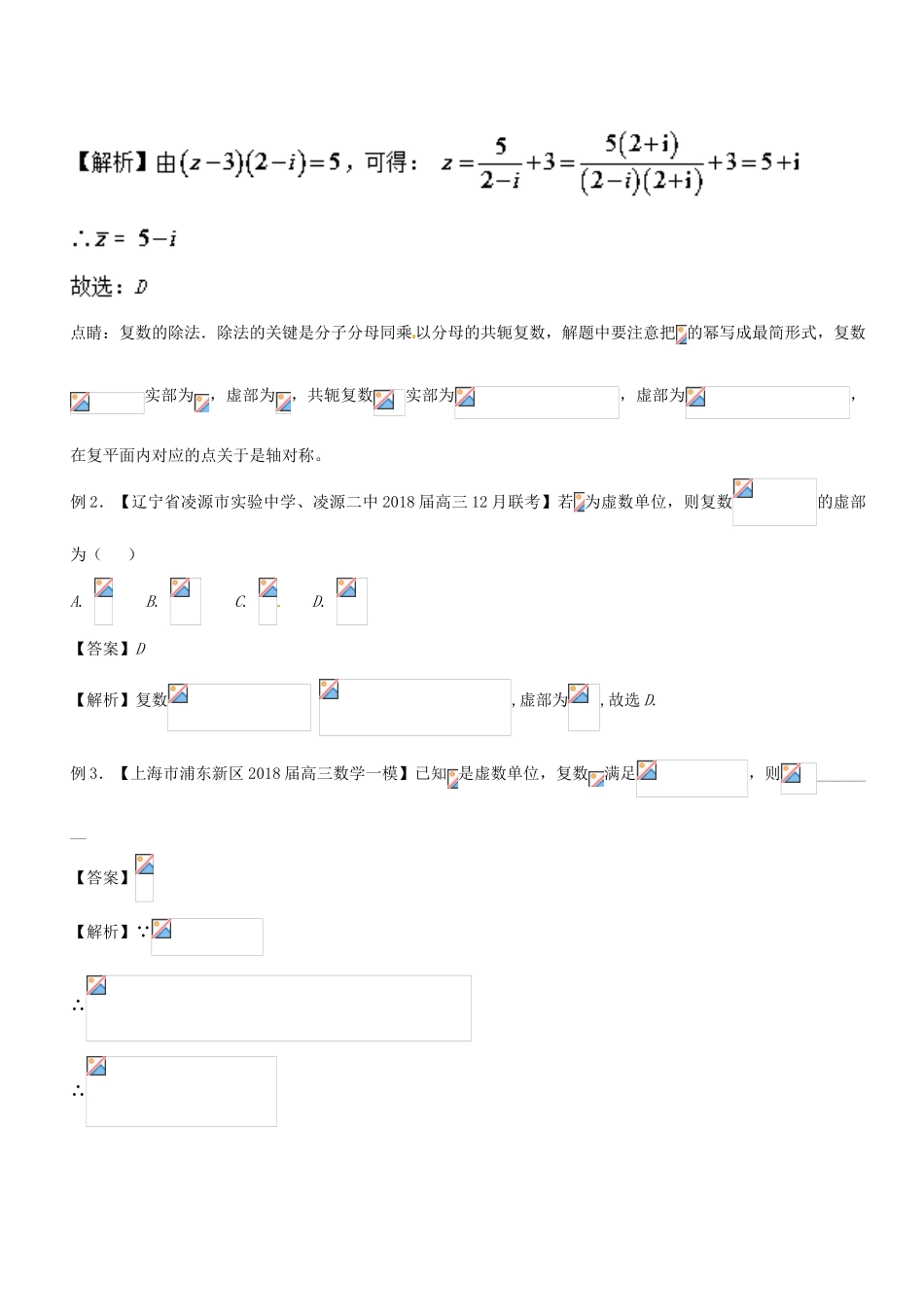
专题75熟记概念方可巧解复数问题考纲要求:1.理解复数的基本概念.理解复数相等的充要条件.2.了解复数的代数表示形式及其几何意义.会进行复数代数形式的四则运算.3.了解复数的代数形式的加、减运算的几何意义.基础知识回顾:一、复数的有关概念1.复数的概念形如a+bi(a,b∈R)的数叫复数,其中a,b分别是它的实部和虚部.若b=0,则a+bi为实数;若b≠0,则a+bi为虚数;若a=0且b≠0,则a+bi为纯虚数.2.复数相等a+bi=c+di⇔a=c且b=d(a,b,c,d∈R).3共轭复数a+bi与c+di共轭⇔a=c,b=-d(a,b,c,d∈R).4.复数的模向量的模r叫做复数z=a+bi(a,b∈R)的模,记作|z|或|a+bi|,即|z|=|a+bi|=.二、复数的几何表示及意义(1)复数z=a+bi复平面内的点Z(a,b)(a,b∈R).(2)复数z=a+bi(a,b∈R)平面向量.三、复数的运算1.复数的乘、除运算法则设z1=a+bi,z2=c+di(a,b,c,d∈R),则(1)乘法:z1·z2=(a+bi)·(c+di)=(ac-bd)+(ad+bc)i;(2)除法:===+i(c+di≠0).2.复数加法的运算定律复数的加法满足交换律、结合律,即对任何z1,z2,z3∈C,有z1+z2=z2+z1,(z1+z2)+z3=z1+(z2+z3).应用举例:类型一复数的概念例1.【2017-2018学年辽宁省沈阳市四校协作体高三年级联合考试】若复数满足(为虚数单位),则的共轭复数为()A.B.C.D.【答案】D点睛:复数的除法.除法的关键是分子分母同乘以分母的共轭复数,解题中要注意把的幂写成最简形式,复数实部为,虚部为,共轭复数实部为,虚部为,在复平面内对应的点关于是轴对称。例2.【辽宁省凌源市实验中学、凌源二中2018届高三12月联考】若为虚数单位,则复数的虚部为()A.B.C.D.【答案】D【解析】复数,虚部为,故选D.例3.【上海市浦东新区2018届高三数学一模】已知是虚数单位,复数满足,则________【答案】【解析】 ∴∴故答案为:类型二复数的几何意义例4.【皖江名校2018届高三12月份大联考】著名数学家欧拉发规了复数的三角形式:(其中为虚数单位,),根据这个公式可知,表示的复数在复平面中所对应的点位于()A.第一象限B.第二象限C.第三象限D.第四象限【答案】B【解析】,3弧度的角终边在第二象限。故选B.例5.【广西钦州市钦州港经济技术开发区中学2018届高三12月月考】复数的共轭复数在复平面上对应的点位于()A.第一象限B.第二象限C.第三象限D.第四象限【答案】B【解析】故选:B点睛:复数代数形式运算问题的常见类型及解题策略:(1)复数的乘法.复数的乘法类似于多项式的四则运算,可将含有虚数单位的看作一类同类项,不含的看作另一类同类项,分别合并即可.(2)复数的除法.除法的关键是分子分母同乘以分母的共轭复数,解题中要注意把的幂写成最简形式.例6.【山东省、湖北省部分重点中学2018届高三第二次联考】已知复数满足,则在复平面内对应的点位于()A.第一象限B.第二象限C.第三象限D.第四象限【答案】B【解析】,则.故选B.类型三复数的运算例7.【广西柳州高级中学、南宁市第二中学2018届高三上学期第二次联考】设是虚数单位,若复数,则()A.B.C.D.【答案】A【解析】因为,所以,故选A.例8.【福建省莆田市第二十四中学2018届高三上学期第二次月考】若,则()A.B.C.D.【答案】C【解析】由题意得,则,故选C.方法、规律归纳:在进行复数的代数运算时,记住以下结论,可提高计算速度.(1)(1±i)2=±2i;=i;=-i;(2)-b+ai=i(a+bi);(3)i4n=1,i4n+1=i,i4n+2=-1,i4n+3=-i,i4n+i4n+1+i4n+2+i4n+3=0,n∈N*.实战演练:1.【江西省南昌市第二中学2018届高三上学期第五次月考】已知(是虚数单位),那么的共轭复数对应的点位于复平面内的()A.第一象限B.第二象限C.第三象限D.第四象限【答案】B【解析】,,的共轭复数对应的点的坐标是,对应的点在第二象限,故选B.2.【2017届吉林省长春市普通高中高三下学期第二次模拟考试】已知复数,则下列命题中正确的是.①;②;.③的虚部为;④在复平面上对应的点位于第一象限.A.1B.2C.3D.4【答案】C【解析】由已知,①②④正确,③错误.故选C.3.【贵州省遵义市遵义四中2018届高三第三次月考】()A....