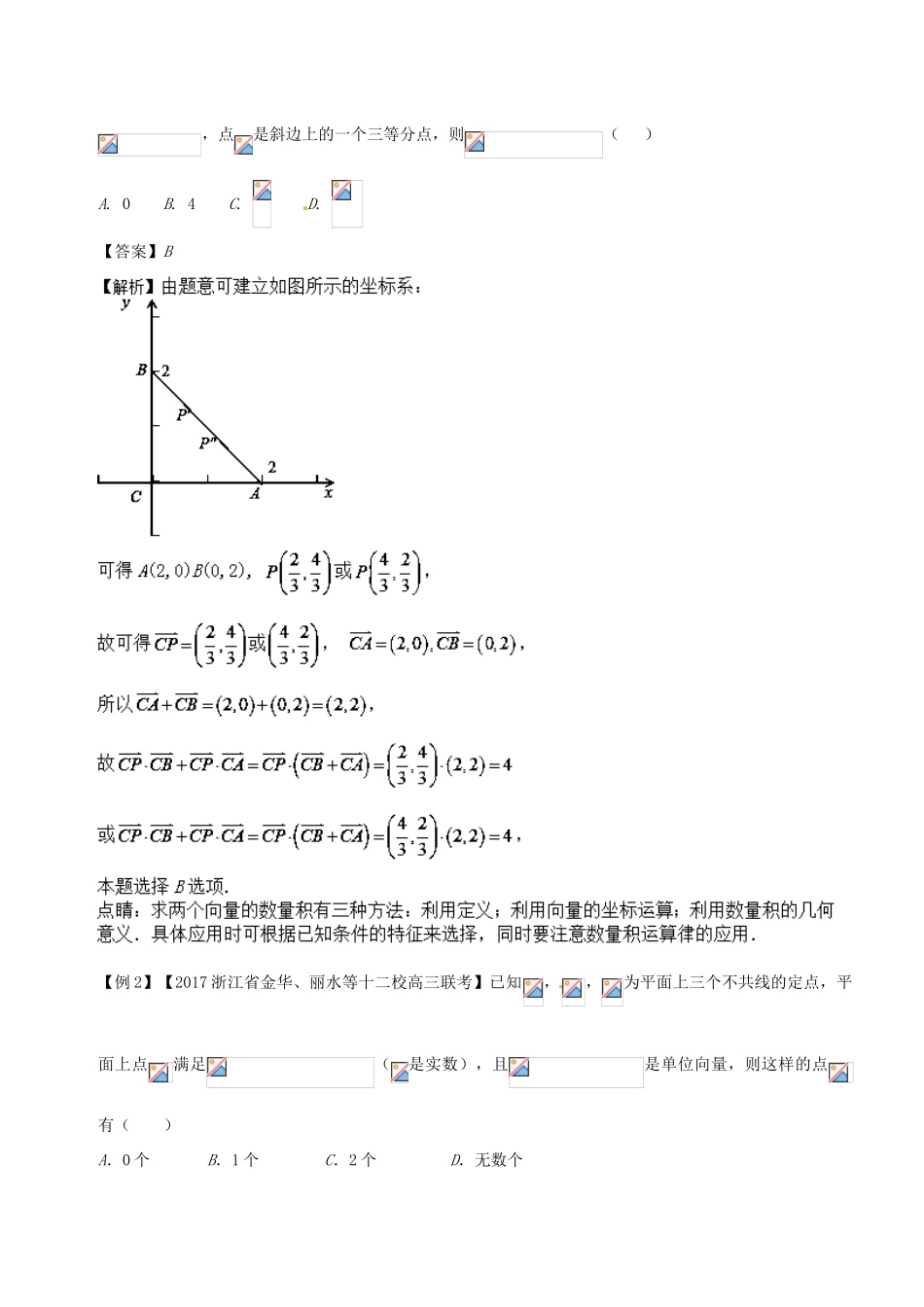
专题30平面向量的几何运算与坐标运算考纲要求:1.理解平面向量数量积的含义及其物理意义,了解平面向量的数量积与向量投影的关系.2.掌握数量积的性质及坐标表达式,会进行平面向量数量积的运算;3.能运用数量积表示两个向量的夹角,会用数量积判断两个平面向量的垂直关系,掌握向量数量积的运算律,并能进行相关计算.基础知识回顾:1.向量的线性运算向量运算定义法则(或几何意义)运算律加法求两个向量和的运算三角形法则平行四边形法则(1)交换律:a+b=b+a;(2)结合律:(a+b)+c=a+(b+c)减法求a与b的相反向量-b的和的运算叫做a与b的差三角形法则a-b=a+(-b)数乘求实数λ与向量a的积的运算(1)|λa|=|λ||a|;(2)当λ>0时,λa的方向与a的方向相同;当λ<0时,λa的方向与a的方向相反;当λ=0时,λa=0λ(μa)=(λμ)a;(λ+μ)a=λa+μa;λ(a+b)=λa+λb2.平面向量的坐标运算(1)向量加法、减法、数乘向量及向量的模:设a=(x1,y1),b=(x2,y2),则a+b=(x1+x2,y1+y2),a-b=(x1-x2,y1-y2),λa=(λx1,λy1),|a|=.(2)向量坐标的求法:①若向量的起点是坐标原点,则终点坐标即为向量的坐标.②设A(x1,y1),B(x2,y2),则=(x2-x1,y2-y1),||=.3.平面向量共线的坐标表示设a=(x1,y1),b=(x2,y2),其中b≠0.a∥b⇔x1y2-x2y1=0.应用举例:类型一、平面向量的线性运算【例1】【河北省武邑中学2018届高三上学期第二次调研】在直角三角形中,角为直角,且,点是斜边上的一个三等分点,则()A.0B.4C.D.【答案】B【例2】【2017浙江省金华、丽水等十二校高三联考】已知,,为平面上三个不共线的定点,平面上点满足(是实数),且是单位向量,则这样的点有()A.0个B.1个C.2个D.无数个【答案】C.【例3】【2017浙江省温州市高三月考试题】如图,矩形中,,,,分别为线段,上的点,且满足,若,则的最小值为_______.【答案】.类型二、平面向量的坐标运算【例4】【2017江苏泰兴中学高三月考】若向量a=(2,1),b=(-1,2),c=,则c可用向量a,b表示为()A.a+bB.-a-bC.a+bD.a-b【答案】A【解析】设c=xa+yb,则=(2x-y,x+2y),所以解得则c=a+b.【例5】【贵州省黔东南州2018届高三上学期第一次联考】若向量,则()A.-36B.36C.12D.-12【答案】D【解析】根据数量积定义知:,故选D.【例6】【贵州省黔东南州2018届高三上学期第一次联考】已知向量,,且,则向量的坐标为()A.B.C.或D.或【答案】C方法、规律归纳:1.向量数量积的两种运算方法(1)当已知向量的模和夹角时,可利用定义法求解,即a·b=|a||b|cosa,b.(2)当已知向量的坐标时,可利用坐标法求解,即若a=(x1,y1),b=(x2,y2),则a·b=x1x2+y1y2.2.平面向量数量积求解问题的策略(1)求两向量的夹角:cosθ=,要注意θ∈[0,π].(2)两非零向量垂直的充要条件是:a⊥b⇔a·b=0⇔|a-b|=|a+b|.(3)求向量的模利用数量积求解长度问题的处理方法有:①a2=a·a=|a|2或|a|=.②|a±b|==.③若a=(x,y),则|a|=.实战演练:1.【广东省兴宁市沐彬中学2018届高三上第二次月考】设若,则m=()A.0B.-3C.D.-7【答案】D【解析】由题意可得,选D.2.【西北师大附中2018届一调】已知向量()A.-3B.2C.3D.-2【答案】A【解析】,选A.3.已知是边长为2的等边三角形,P为平面ABC内一点,则的最小值是()A.B.C.D.【答案】B4.【河北省武邑中学2018届高三上学期第二次调研】已知向量,,则向量与的夹角为()A.135°B.60°C.45°D.30°【答案】C【解析】由题意可得:,则:,且,设所求解的向量的夹角为,由题意可得:,则:向量与的夹角为45°.本题选择C选项.5.已知()A.B.C.-D.【答案】B6.已知点O是边长为1的等边三角形ABC的中心,则等于A.B.C.D.【答案】D【解析】由于点O是边长为1的等边△ABC的中心,D为BC的中点,,,两两夹角为120°.所以.所以。故选D.7.分别是的中线,若,且与的夹角为,则=()A.B.C.D.【答案】C【解析】由解得.故选C.点睛:平面向量的数量积计算问题,往往有两种形式,一是利用数量积的定义式,二是利用数量积的坐标运算公式,涉及几何图形的问题...