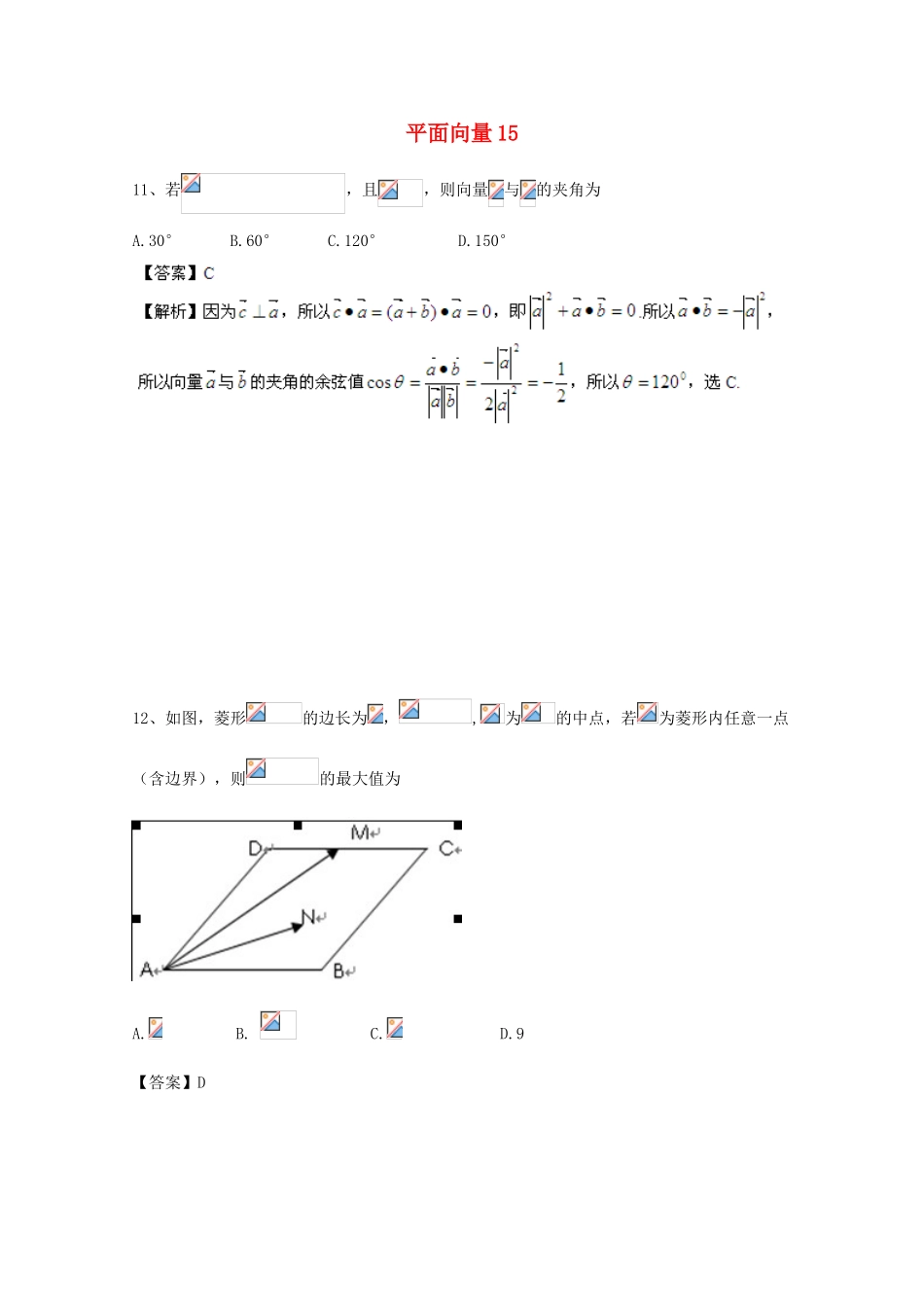
平面向量1511、若,且,则向量与的夹角为A.30°B.60°C.120°D.150°12、如图,菱形的边长为,,为的中点,若为菱形内任意一点(含边界),则的最大值为A.B.C.D.9【答案】D【解析】13、已知向量且,若变量x,y满足约束条件,则z的最大值为A.1B.2C.3D.4答案:C解析:由得(,1)(2,)=0,即z=2x+y,画出不等式组的可行域,如右图,目标函数变为:,作出y=-2x的图象,并平移,图由可知,直线过A点时,在y轴上的截距最大,此时z的值最大:求出A点坐标(1,1)=2×1+1=3,所以,选C。14已知平面向量,满足与的夹角为,则“m=1”是“”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件15.如图所示,已知则下列等式中成立的是(A)(B)(C)(D)16.的外接圆的圆心为O,半径为1,若,且,则向量在向量方向上的射影的数量为()(A).(B).(C).3(D).【答案】A【解析】由已知可以知道,的外接圆的圆心在线段BC的中点O处,因此是直角三角形。且,又因为因此答案为A17.若,恒成立,则△ABC的形状一定是()A.锐角三角形B.直角三角形C.钝角三角形D.不能确定18.关于的方程,(其中、、都是非零平面向量),且、不共线,则该方程的解的情况是A.至多有一个解B.至少有一个解C.至多有两个解D.可能有无数个解19.已知向量a=(1,2),b=(2,0),若向量λa+b与向量c=(1,-2)共线,则实数λ等于A.-2B.-C.-1D.-【答案】C【解析】本题主要考查平面向量的共线的性质.属于基础知识、基本运算的考查.λa+b=(λ+2,2λ),向量λa+b与向量c=(1,-2)共线,∴(λ+2)×(-2)=2λ×1,∴λ=-120.如图,已知,,·,∠AOP=,若,则实数t等于A.B.C.D.321.△ABC中,∠C=90°,且CA=CB=3,点M满足2,则·=A.18B.3C.15D.12【答案】A【解析】本题主要考查平面向量的共线及数量积的基本运算.属于基础知识、基本运算的考查.由题意,如图建立直角坐标系,则A(3,0),B(0,3)∵2,∴A是BM的中点∴M(6,-3)=(6,-3),=(3,0)·=18